题解：P3371 【模板】单源最短路径（弱化版）

题目都说了可以用 SPFA 啊，秀啥 Dijkstra 啊！

先介绍一下 SPFA 死了的算法。

SPFA 算法，全名 Shortest Path Faster Algorithm，是一种用于解决单源最短路径问题的算法，它是 Bellman-Ford 算法的改进版本。SPFA 算法可以处理带有负权边的图，但不能处理带有负权环的图。算法的基本思想是使用一个队列来存储所有待优化的节点，并通过不断的松弛操作来逼近最短路径。

注：来源于网络。

SPFA 的基本步骤

1. 初始化答案数组，全部设为无穷大。

2. 将源点加入队列，打上在队列的标记，将到起点的答案设为 \(0\)。

3. 队列非空时，取出队首元素存下后立即取消标记并弹出队首元素，并对其所有出边进行松弛操作。

4. 如果松弛成功，并且终点不在队列中，则将终点加入队列并打上在队列的标记。

5. 重复步骤 \(3\) 和 \(4\)，直到队列为空。

手玩一下样例

样例如图

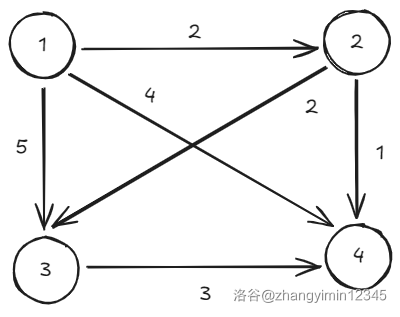
将答案数组记作 dis，是否在队列的标记数组记作 vis。

最开始的 dis 与 vis 如下图。

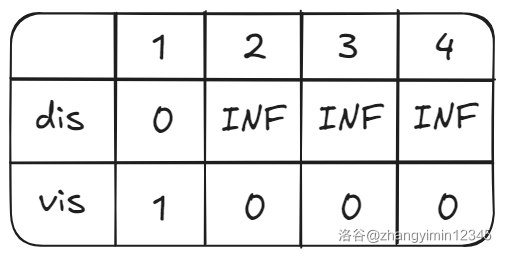
最开始的队列如下图。

第一轮，取队首元素 \(1\)，此时 \(1\) 能松弛 \(2\)、\(3\)、\(4\)，且 \(2\)、\(3\)、\(4\) 都不在队列中，都没打标记，所以将这几个数全部扔进队列并打上标记。

此时的 dis、vis、队列如下图。

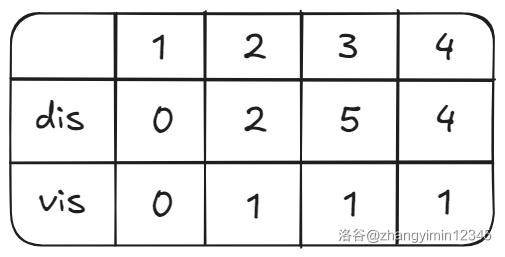
第二轮，取队首元素 \(2\)，此时 \(2\) 能松弛 \(3\) 和 \(4\)，但 \(3\) 和 \(4\) 都在队列中，都打了标记，所以不再扔进队列。

此时的 dis、vis、队列如下图。

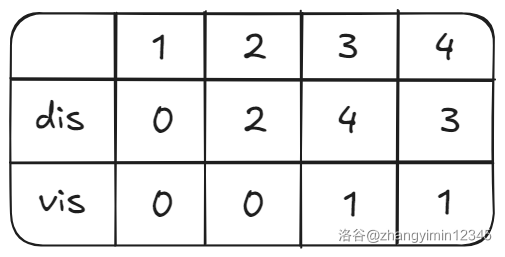
第三轮，取队首元素 \(3\)，此时 \(3\) 不能松弛任何一个点。

此时的 dis、vis、队列如下图。

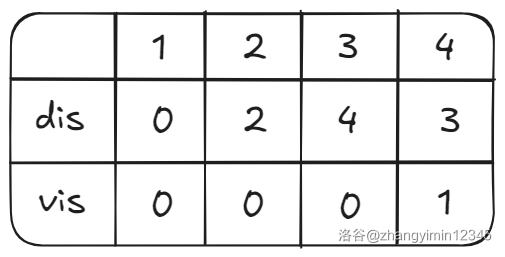
第三轮，取队首元素 \(4\)，此时 \(4\) 不能松弛任何一个点。

此时的 dis、vis、队列如下图。

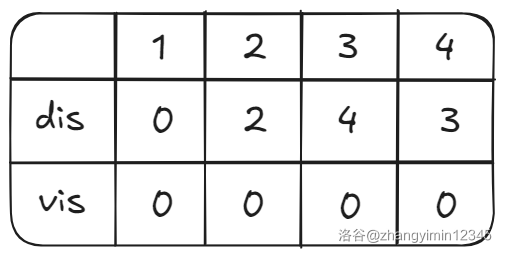
此时队列已经空了，结束。

放代码

# include <bits/stdc++.h>
using namespace std;
int n , m , s , u , v , w , dis[10010];
bool vis[10010];
vector <pair <int , int> > g[10010];
void bfs()
{
    for(int i = 1 ; i <= n ; i ++)
    {
        dis[i] = 1e9;
    }
    queue <int> q;
    q.push(s);
    vis[s] = 1;
    dis[s] = 0;
    while(!q.empty())
    {
        int t = q.front();
        q.pop();
        vis[t] = 0;
        for(int i = 0 ; i < g[t].size() ; i ++)
        {
            if(dis[g[t][i].first] > dis[t] + g[t][i].second)
            {
                dis[g[t][i].first] = dis[t] + g[t][i].second;
                if(vis[g[t][i].first])
                {
                    continue;
                }
                vis[g[t][i].first] = 1;
                q.push(g[t][i].first);
            }
        }
    }
    return ;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m >> s;
    for(int i = 1 ; i <= m ; i ++)
    {
        cin >> u >> v >> w;
        g[u].push_back({v , w});
    }
    bfs();
    for(int i = 1 ; i <= n ; i ++)
    {
        if(dis[i] == 1e9)
        {
            cout << (1LL << 31) - 1 << " ";
        }
        else
        {
            cout << dis[i] << " ";
        }
    }
    return 0;
}