求最大公约数伪代码
1. 上网查找什么是求两个数的最大公约数的欧几里得算法(辗转相除法),提交算法说明和网上链接。
2. 参考教材,用伪代码(英语或汉语)实现欧几里得算法(辗转相除法),提交伪代码。
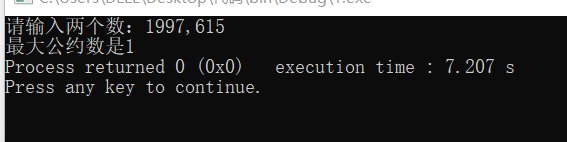
3. 选择几组数据,手动走一下伪代码,测试你写的伪代码是否正确,提交测试过程截图。
1.什么是求两个数的最大公约数的欧几里得算法(辗转相除法)
欧几里得算法是用来求两个正整数最大公约数的算法。古希腊数学家欧几里得在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里得算法。
扩展欧几里得算法可用于RSA加密等领域。
假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里得算法,是这样进行的:
1997 / 615 = 3 (余 152)
615 / 152 = 4(余7)
152 / 7 = 21(余5)
7 / 5 = 1 (余2)
5 / 2 = 2 (余1)
2 / 1 = 2 (余0)
至此,最大公约数为1
以除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公约数,所以就得出了 1997 和 615 的最大公约数 1。
参考资料百度百科
2.伪代码
Write "n"
Read n
Write "m"
Read m
Set quotient to 1
WHILE (quotient is not zero)
Set quotient to m DIV n
Set m to quotient
Else
Make the quotient in the answer
Write "The answer is "
Write answer3.测试
#include <stdio.h>
int main()
{
int m,n,c;
printf("请输入两个数:");
scanf("%d,%d",&m,&n);
while(n != 0)
{
c = m % n;
m = n;
n = c;
}
printf("最大公约数是%d",m);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号