【做题记录】图论(马思博)
A. Dominant Indices
设 \(f_{u,i}\) 表示 \(u\) 子树中距离 \(u\) 为 \(i\) 的点数,有 \(f_{u,i}=\sum f_{v,i-1}\),在转移过程中维护答案。直接转移是 \(O(n^2)\) 的,于是需要长链剖分优化。具体地,每个点继承长儿子的 DP 数组,然后再将轻儿子合并上去。使用指针即可,时空复杂度都线性。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=1e6+5;
int n,dep[maxn],mxd[maxn],des[maxn],len[maxn];
int dp[maxn],*cnt=dp,*f[maxn],ans[maxn];
vector<int> e[maxn];
il void dfs1(int u,int fa){
mxd[u]=dep[u]=dep[fa]+1;
for(int v:e[u]){
if(v==fa){
continue;
}
dfs1(v,u);
if(mxd[v]>mxd[u]){
mxd[u]=mxd[v];
des[u]=v;
}
}
}
il void dfs2(int u,int fa){
if(!f[u]){
len[u]=mxd[u]-dep[u];
f[u]=cnt,cnt+=len[u]+1;
}
f[u][0]=1,ans[u]=0;
if(des[u]){
f[des[u]]=f[u]+1;
dfs2(des[u],u);
if(f[u][ans[des[u]]+1]>1){
ans[u]=ans[des[u]]+1;
}
}
for(int v:e[u]){
if(v==fa||v==des[u]){
continue;
}
dfs2(v,u);
for(int i=0;i<=len[v];i++){
f[u][i+1]+=f[v][i];
if(f[u][i+1]>f[u][ans[u]]||f[u][i+1]==f[u][ans[u]]&&i+1<ans[u]){
ans[u]=i+1;
}
}
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].pb(v),e[v].pb(u);
}
dfs1(1,0),dfs2(1,0);
for(int i=1;i<=n;i++){
cout<<ans[i]<<"\n";
}
return 0;
}
}
int main(){return asbt::main();}
B. [国家集训队] 墨墨的等式
考虑差分,于是问题变为 \([0,x]\) 中有多少能被拼出来。设 \(m=\min\{a_i\}\),那么如果 \(w\) 能被拼出来,\(w+mk\;(k\in\mathbb{N})\) 一定能被拼出来。于是对于每个 \(i<m\),我们只需求出最小的 \(w\equiv i\pmod{m}\) 使得 \(w\) 能被拼出,则在模 \(m\) 余 \(i\) 的剩余系中的答案就是 \(\lfloor\frac{x-w}{m}\rfloor+1\)(当然前提是 \(w\le x\))。
考虑建图,对于 \(i<m\),连一条 \(i\xrightarrow{a_j}(i+a_j)\bmod m\) 的有向边。于是从 \(0\) 跑一遍最短路,\(dis_i\) 就是 \(w\)。
这个算法即为同余最短路。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
#define pb push_back
#define pii pair<int,int>
#define fir first
#define sec second
#define mp make_pair
using namespace std;
namespace asbt{
const int maxn=5e5+5,inf=1e9;
int n,m=inf,l,r,a[17],dis[maxn];
bool vis[maxn];
vector<pii> e[maxn];
priority_queue<pii> q;
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>l>>r;
for(int i=1;i<=n;i++){
cin>>a[i];
if(a[i]){
m=min(m,a[i]);
}
}
for(int i=0;i<m;i++){
for(int j=1;j<=n;j++){
e[i].pb(mp((i+a[j])%m,a[j]));
}
}
memset(dis,0x3f,sizeof(dis));
dis[0]=0,q.push(mp(0,0));
while(q.size()){
int u=q.top().sec;
q.pop();
if(vis[u]){
continue;
}
vis[u]=1;
for(pii i:e[u]){
int v=i.fir,w=i.sec;
if(!vis[v]&&dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
q.push(mp(-dis[v],v));
}
}
}
int ans=0;
l--;
for(int i=0;i<m;i++){
if(dis[i]<=r){
ans+=(r-dis[i])/m+1;
}
if(dis[i]<=l){
ans-=(l-dis[i])/m+1;
}
}
cout<<ans;
return 0;
}
}
signed main(){return asbt::main();}
C. Xor-MST
首先将所有点扔到 01-trie 里。贪心地想,两个连通块必然在深度尽可能深的位置合并。对于每个结点,暴力计算它的两个子树的最小异或和即可。时间复杂度线性对数方。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=2e5+5;
int n,rt=1,tot=1,tr[maxn<<5][2];
ll ans;
il int calc(int p,int q,int d){
if(d==-1){
return 0;
}
if(tr[p][0]&&tr[p][1]){
if(tr[q][0]&&tr[q][1]){
return min(calc(tr[p][0],tr[q][0],d-1),calc(tr[p][1],tr[q][1],d-1));
}else if(tr[q][0]){
return calc(tr[p][0],tr[q][0],d-1);
}else{
return calc(tr[p][1],tr[q][1],d-1);
}
}else if(tr[p][0]){
if(tr[q][0]&&tr[q][1]){
return calc(tr[p][0],tr[q][0],d-1);
}else if(tr[q][0]){
return calc(tr[p][0],tr[q][0],d-1);
}else{
return calc(tr[p][0],tr[q][1],d-1)+(1<<d);
}
}else{
if(tr[q][0]&&tr[q][1]){
return calc(tr[p][1],tr[q][1],d-1);
}else if(tr[q][0]){
return calc(tr[p][1],tr[q][0],d-1)+(1<<d);
}else{
return calc(tr[p][1],tr[q][1],d-1);
}
}
}
il void solve(int p,int d){
if(!p){
return ;
}
if(d){
solve(tr[p][0],d-1);
solve(tr[p][1],d-1);
}
if(tr[p][0]&&tr[p][1]){
ans+=calc(tr[p][0],tr[p][1],d-1)+(1<<d);
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1,x;i<=n;i++){
cin>>x;
int p=rt;
for(int j=29;~j;j--){
int t=x>>j&1;
if(!tr[p][t]){
tr[p][t]=++tot;
}
p=tr[p][t];
}
}
solve(rt,29);
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
D. Kuroni and Antihype
先将原题转化,每次要加入一个点 \(u\),若有与之按位与为 \(0\) 的已经加入的 \(v\) 则将答案累加 \(a_v\),否则不累加答案。
令 \(a_{n+1}=0\),并钦定 \(n+1\) 已经加入,于是对于每个点 \(u\) 都有对应的 \(v\)。考虑在 \(u\) 加入时连一条边 \(u\xleftrightarrow{a_u+a_v}v\),于是我们所求即为最大生成树再减去所有点权之和。边数很多,显然不能直接建边。考虑 \(a_u\operatorname{and} a_v=0\),于是 \(a_u+a_v=a_u\operatorname{or}a_v\)。考虑从大到小枚举边权 \(i\),再枚举 \(i\) 的子集 \(j\),此时所有点权为 \(j\) 的和所有点权为 \(i\oplus j\) 的点可以连边,用并查集维护即可。时间复杂度 \(O(3^{18}\alpha(n))\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=3e5+5,N=(1<<18)-1;
int n,cnt[maxn],fa[maxn];
ll ans;
il int find(int x){
return x!=fa[x]?fa[x]=find(fa[x]):x;
}
il void merge(int u,int v,int w){
u=find(u),v=find(v);
if(u==v){
return ;
}
ans+=(cnt[u]+cnt[v]-1)*1ll*w;
fa[u]=v,cnt[v]=1;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n,cnt[0]=1;
for(int i=1,x;i<=n;i++){
cin>>x,cnt[x]++,ans-=x;
}
for(int i=0;i<=N;i++){
fa[i]=i;
}
for(int i=N;i;i--){
for(int j=i;j;j=(j-1)&i){
if(cnt[j]&&cnt[i^j]){
merge(j,i^j,i);
}
}
}
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
E. [BalkanOI 2011] timeismoney
考虑对于每一棵生成树记一个点 \((\sum a,\sum b)\),于是所有有可能成为答案的点都在一个下凸包上。证明如下:

如图,\(A-B-C-D-E\) 组成了一个下凸包,对于其外的 \(F\),\(OF\) 与 \(A-B-C-D-E\) 的交点 \(G\) 比 \(F\) 优。对于过 \(B\) 的反比例函数 \(f\),其与 \(OF\) 的交点 \(H\) 又比 \(G\) 优,而 \(H\) 和 \(B\) 又是等同的,所以最优点一定在下凸包 \(A-B-C-D-E\) 上。
根据这里的证明,凸包上的点数最多为 \(O((na)^{\frac{2}{3}})\) 个。现在的问题是怎么找到这些点。
首先我们先找到 \(x\) 最小的点 \(A\) 和 \(y\) 最小的点 \(E\),然后去找凸包上 \(AE\) 这一段中离 \(AE\) 最远的点 \(B\)。显然 \(B\) 在 \(AE\) 左侧,且 \(B\) 到 \(AE\) 的距离最大,也就是 \(\overrightarrow{AE}\times\overrightarrow{AB}\) 最小。有:
于是我们最小化 \((x_E-x_A)y_B+(y_A-y_E)x_B\) 即可,将边权设为 \((x_E-x_A)b+(y_A-y_E)a\) 跑 kurskal 就好了。然后递归 \(AB\) 和 \(BE\) 即可。时间复杂度 \(O((na)^{\frac{2}{3}}m\log m)\)。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e4+5;
int n,m,fa[205];
struct edge{
int u,v,a,b,w;
il bool operator<(const edge &x)const{
return w<x.w;
}
}a[maxn];
struct node{
int x,y;
node(int x=0,int y=0):x(x),y(y){}
il node operator-(const node &b)const{
return node(x-b.x,y-b.y);
}
il int operator*(const node &b)const{
return x*b.y-y*b.x;
}
il bool operator<(const node &b)const{
return x*y<b.x*b.y||x*y==b.x*b.y&&x<b.x;
}
}ans;
il int find(int x){
return x!=fa[x]?fa[x]=find(fa[x]):x;
}
il node mst(){
for(int i=1;i<=n;i++){
fa[i]=i;
}
sort(a+1,a+m+1);
int x=0,y=0;
for(int i=1,u,v;i<=m;i++){
u=find(a[i].u),v=find(a[i].v);
if(u!=v){
fa[u]=v;
x+=a[i].a,y+=a[i].b;
}
}
return node(x,y);
}
il void solve(node A,node B){
for(int i=1;i<=m;i++){
a[i].w=(B.x-A.x)*a[i].b+(A.y-B.y)*a[i].a;
}
node C=mst();
if((B-A)*(C-A)==0){
return ;
}
ans=min(ans,C);
solve(A,C),solve(C,B);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>a[i].u>>a[i].v>>a[i].a>>a[i].b;
a[i].u++,a[i].v++;
}
for(int i=1;i<=m;i++){
a[i].w=a[i].a;
}
node A=mst();
for(int i=1;i<=m;i++){
a[i].w=a[i].b;
}
node B=mst();
ans=min(A,B);
solve(A,B);
cout<<ans.x<<' '<<ans.y;
return 0;
}
}
signed main(){return asbt::main();}
M. [POI 2014] HOT-Hotels 加强版
首先考虑合法的 \((i,j,k)\) 的形态,可以想到这样两种:
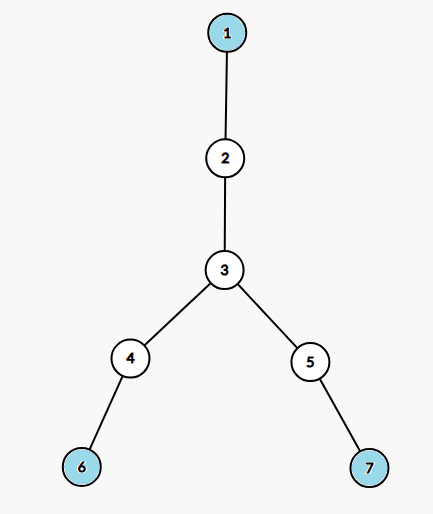
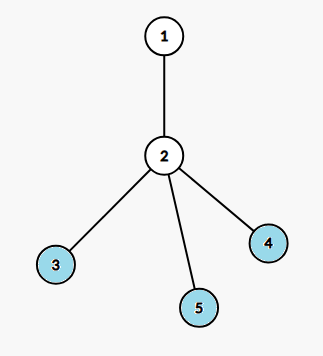
可以想到设 \(f_{u,i}\) 表示 \(u\) 子树中距离 \(u\) 为 \(i\) 的点的个数,长剖优化是显然的,但是优化后难以直接计算第二种情况。于是再设 \(g_{u,i}\) 表示 \(u\) 子树内满足 \(\operatorname{dis}(\operatorname{lca}(x,y),x)=\operatorname{dis}(\operatorname{lca}(x,y),y)=\operatorname{dis}(\operatorname{lca}(x,y),u)+i\) 的 \((x,y)\) 的数量,于是有转移:\(g_{u,i}=\sum\limits_{v}g_{v,i+1}+\sum\limits_{x,y}f_{x,i-1}\times f_{y,i-1}\)。于是长剖优化即可,时空都线性,注意 \(g\) 数组要开两倍。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=1e5+5;
int n,mxd[maxn],dep[maxn],des[maxn],len[maxn];
int F[maxn],*cf=F,*f[maxn];
ll G[maxn<<1],*cg=G,*g[maxn],ans;
vector<int> e[maxn];
il void dfs1(int u,int fa){
mxd[u]=dep[u]=dep[fa]+1;
for(int v:e[u]){
if(v==fa){
continue;
}
dfs1(v,u);
if(mxd[u]<mxd[v]){
mxd[u]=mxd[v],des[u]=v;
}
}
}
il void dfs2(int u,int fa){
if(!f[u]){
len[u]=mxd[u]-dep[u]+1;
f[u]=cf,cf+=len[u];
g[u]=cg+len[u],cg+=len[u]<<1;
}
f[u][0]=1;
if(des[u]){
int v=des[u];
f[v]=f[u]+1,g[v]=g[u]-1;
dfs2(v,u);
}
ans+=g[u][0];
for(int v:e[u]){
if(v==fa||v==des[u]){
continue;
}
dfs2(v,u);
for(int i=0;i<len[v];i++){
if(i){
ans+=g[v][i]*f[u][i-1];
}
ans+=f[v][i]*g[u][i+1];
}
for(int i=0;i<len[v];i++){
if(i){
g[u][i-1]+=g[v][i];
}
g[u][i+1]+=f[u][i+1]*1ll*f[v][i];
f[u][i+1]+=f[v][i];
}
}
// cout<<u<<":\n";
// for(int i=0;i<len[u];i++){
// cout<<f[u][i]<<' ';
// }
// cout<<'\n';
// for(int i=0;i<len[u];i++){
// cout<<g[u][i]<<' ';
// }
// cout<<'\n';
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].pb(v),e[v].pb(u);
}
dfs1(1,0),dfs2(1,0);
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
O. [agc057_d]Sum Avoidance
比较复杂。
Theorem 1:题目所求的 \(A\) 满足 \(|A|=\lfloor\frac{S-1}{2}\rfloor\)。
Proof 1:
Lemma A:\(|A|\le\lfloor\frac{S-1}{2}\rfloor\)。
Proof A:考虑 \(1\) 到 \(S-1\) 共 \(S-1\) 个数。根据鸽巢原理,若 \(|A|>\lfloor\frac{S-1}{2}\rfloor\) 那么必然存在 \(v\) 使得 \(v\) 和 \(S-v\) 被同时选入,矛盾。
于是考虑后 \(\lfloor\frac{S-1}{2}\rfloor\) 个数,它们两两之和都大于 \(S\)。于是得证。
考虑设 \(A\) 中 \(\le\lfloor\frac{S-1}{2}\rfloor\) 的数组成的集合为 \(B\),于是我们可以在知道 \(B\) 的情况下还原 \(A\)。
Theorem 2:若 \(a,b\in B,a+b\le\lfloor\frac{S-1}{2}\rfloor\),那么 \(a+b\in B\)。
Proof 2:若 \(a+b\notin B\),那么由 Theorem 1 必有 \(S-a-b\in A\),于是 \(A\) 不合法。
Theorem 3:若 \(B\) 合法,则 \(A\) 合法。
Proof 3:若 \(A\) 不合法,则在 \(A\) 中必然存在 \(x>\lfloor\frac{S-1}{2}\rfloor\) 且能与 \(B\) 中若干个数组成 \(S\)。换句话说,\(S-x\notin B\) 并且 \(B\) 中若干个数可以组成 \(S-x\),与 Theorem 2 矛盾。
那么考虑最小化 \(B\) 的字典序即可。一个显然的贪心是从小到大枚举每一个数,如果加入后合法便加入。考虑第一个被加进去的数 \(d\),它满足 \(\operatorname{lcm}(1,2,\dots,d-1)|S\)。发现 \(d\le43\)。
于是对于每个被加进去的数,分两类:
- 能被 \(B\) 中的数表示,于是必须加入。
- 不能被表示,但是加入后仍然合法,于是加入。
从模 \(d\) 的剩余系考虑,若 \(x\) 以第二种方式被加入,则必然与 \(B\) 中现有的数不同余。因此至多有 \(d\) 个数以第二种方式加入。
考虑怎么快速地维护 \(B\)。考虑一个类同余最短路状物,设 \(f_i\) 表示能表示出的模 \(d\) 等于 \(i\) 的数的最小值。于是我们得到 \(f\) 就可还原出 \(B\),这将在后面说明。
考虑加入数对 \(f\) 的影响。第一种方式不会影响 \(B\),而第二种方式会影响。具体地,\(\forall x\in[0,d),i\in[1,d),f_{(x+iv)\bmod d}\leftarrow f_x+iv\)。
考虑求出 \(v\)。首先需要满足 \(v<f_{v\bmod d}\),然后需要满足用 \(v\) 更新后 \(f_{S\bmod d}>S\)。枚举 \(x=v\bmod d\),于是可以求出 \(v\) 的下界:
于是 \(v=\min v_x\),再用 \(v\) 更新 \(f\) 即可。这一部分时间复杂度 \(O(d^3)\)。
考虑用 \(f\) 数组求答案。对于 \(x\le\lfloor\frac{S-1}{2}\rfloor\),可以求出 \(B\) 中 \(\le x\) 的数的数量:
于是二分即可。这一部分时间复杂度 \(O(d\log S)\)。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
using namespace std;
namespace asbt{
const int inf=2e18;
int T,S,K,d,f[49];
il int count(int x){
int cnt=0;
for(int i=0;i<d;i++){
if(x>=f[i]){
cnt+=(x-f[i])/d+(i>0);
}
}
return cnt;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>S>>K;
if(K>(S-1)>>1){
cout<<-1<<'\n';
continue;
}
d=1;
while(S%d==0){
d++;
}
memset(f,0x3f,sizeof(f));
f[0]=0;
while(1){
int v=inf;
for(int i=1;i<d;i++){
int t=0;
for(int j=1;j<d;j++){
t=max(t,(S-f[((S-i*j)%d+d)%d])/j+1);
}
while(t%d!=i){
t++;
}
if(t<f[i]){
v=min(v,t);
}
}
if(v>(S-1)>>1){
break;
}
for(int i=0;i<d;i++){
int t=i;
do{
int x=(t+v)%d;
f[x]=min(f[x],f[t]+v);
t=x;
}while(t!=i);
}
}
if(count((S-1)>>1)>=K){
int l=1,r=(S-1)>>1;
while(l<r){
int mid=(l+r)>>1;
if(count(mid)>=K){
r=mid;
}
else{
l=mid+1;
}
}
cout<<l<<'\n';
}else{
int l=S-(S-1)/2,r=S-1;
while(l<r){
int mid=(l+r)>>1;
if((S-1)/2-(S-mid-1-count(S-mid-1))>=K){
r=mid;
}
else{
l=mid+1;
}
}
cout<<l<<'\n';
}
}
return 0;
}
}
signed main(){return asbt::main();}
P. Team Players
考虑容斥。设至少有 \(0\) 条连边的三元组的贡献和为 \(c0\),类似地有 \(c1,c2,c3\),于是答案为 \(c0-c1+c2-c3\)。
对于 \(c0\),考虑每个 \(u\) 的贡献,即考虑另外两个数与 \(u\) 的大小关系。于是贡献为:\(c{u\choose2}+bu(n-u-1)+a{n-u-1\choose2}\)。
对于 \(c1\),枚举每一条边 \((u,v)\),不妨令 \(u<v\),考虑第三个数 \(t\) 与 \(u,v\) 的关系即可。
对于 \(c2\),考虑枚举每个点的出边。对于 \(u\) 的所有出边 \((u,v)\),假设 \(v\) 的排名是 \(i\)(从 \(0\) 开始),于是 \(v\) 的贡献可以分两类讨论:
-
\(v>u\),贡献为 \(ivc+(d_u-i-1)vb\)。
-
\(v<u\),贡献为 \(ivb+(d_u-i-1)va\)。
而 \(u\) 的贡献,假设有 \(l\) 个点比 \(u\) 小,\(r\) 个点比 \(u\) 大,于是贡献为 \(cu{l\choose2}+lrub+au{r\choose2}\)。
对于 \(c3\),其实质是一个三元环计数。考虑将无向图转为有向图,每条边指向度数更大的那一个点,于是每个点的出度显然 \(\le\sqrt{m}\)。此时再枚举每一条边 \((u,v)\),求出 \(u\) 和 \(v\) 能共同到的点即可。
总时间复杂度 \(O(n+m+m\log m+m\sqrt{m})\)。
Code
#include<bits/stdc++.h>
#define int unsigned long long
#define il inline
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=2e5+5;
int n,m,a,b,c,d[maxn];
bool vis[maxn];
vector<int> e[maxn];
struct{
int u,v;
}E[maxn];
il int calc0(){
int res=0;
for(int i=0;i<n;i++){
res+=(n-i-1)*(n-i-2)/2*a*i;
res+=i*(n-i-1)*b*i;
res+=i*(i-1)/2*c*i;
}
// cout<<0<<' '<<res<<'\n';
return res;
}
il int calc1(){
int res=0;
for(int i=1;i<=m;i++){
int u=E[i].u,v=E[i].v;
res+=u*(u-1)/2*a+u*u*b+v*u*c;
res+=u*(v-u-1)*a+(u+v)*(v-u-1)/2*b+v*(v-u-1)*c;
res+=u*(n-v-1)*a+v*(n-v-1)*b+(v+n)*(n-v-1)/2*c;
}
// cout<<1<<' '<<res<<'\n';
return res;
}
il int calc2(){
int res=0;
for(int u=0;u<n;u++){
sort(e[u].begin(),e[u].end());
int l=0,r=d[u];
for(int i=0;i<d[u];i++){
int v=e[u][i];
if(v<u){
l++,r--;
}
if(u<v){
res+=i*v*c+(d[u]-i-1)*v*b;
}else{
res+=i*v*b+(d[u]-i-1)*v*a;
}
}
res+=l*(l-1)/2*u*c+l*r*u*b+r*(r-1)/2*u*a;
}
// cout<<2<<' '<<res<<'\n';
return res;
}
il int calc3(){
for(int u=0;u<n;u++){
e[u].clear();
}
for(int i=1;i<=m;i++){
int u=E[i].u,v=E[i].v;
if(d[u]<d[v]||d[u]==d[v]&&u<v);
else{
swap(u,v);
}
e[u].pb(v);
}
int res=0;
for(int u=0;u<n;u++){
for(int v:e[u]){
vis[v]=1;
}
for(int v:e[u]){
for(int x:e[v]){
if(vis[x]){
int hp[3]={u,v,x};
sort(hp,hp+3);
res+=a*hp[0]+b*hp[1]+c*hp[2];
}
}
}
for(int v:e[u]){
vis[v]=0;
}
}
// cout<<3<<' '<<res<<'\n';
return res;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m>>a>>b>>c;
for(int i=1,u,v;i<=m;i++){
cin>>u>>v;
if(u>v){
swap(u,v);
}
E[i]={u,v},d[u]++,d[v]++;
e[u].pb(v);
e[v].pb(u);
}
// cout<<calc0()<<' '<<calc1()<<' '<<calc2()<<' '<<calc3();
cout<<calc0()-calc1()+calc2()-calc3();
return 0;
}
}
signed main(){return asbt::main();}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号