【比赛记录】2025CSP-S模拟赛28
| A | B | C | D | Sum | Rank |
|---|---|---|---|---|---|
| 30 | 10 | 20 | 15 | 75 | 7/18 |
A. 路径
看到 DAG,不难想到拓扑排序。考虑在拓扑排序的过程中记录每个点的深度 \(dep\)。不难想到如果有两个点在同一深度,则不合法。但这样的做法不完全。首先每个点可能有多条边指向它,导致它的深度不确定;其次一些错误状态可能被算作正确(如下图)。
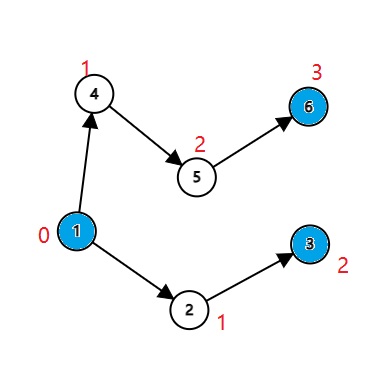
于是我们只在关键点使深度变大,同时每个点的深度取最大的那个(即从哪个关键点过来),即可判断。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=1e6+5;
int T,n,m,kk,a[maxn],deg[maxn],dep[maxn];
bool f[maxn],g[maxn];
vector<int> e[maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>n>>m;
for(int i=1,u,v;i<=m;i++){
cin>>u>>v;
e[u].pb(v),deg[v]++;
}
cin>>kk;
for(int i=1;i<=kk;i++){
cin>>a[i];
f[a[i]]=1;
}
queue<int> q;
for(int i=1;i<=n;i++){
if(!deg[i]){
q.push(i);
dep[i]=f[i];
}
}
while(q.size()){
int u=q.front();
q.pop();
for(int v:e[u]){
dep[v]=max(dep[u]+f[v],dep[v]);
if(--deg[v]==0){
q.push(v);
}
}
}
for(int i=1;i<=kk;i++){
if(g[dep[a[i]]]){
cout<<"No\n";
goto togo;
}
g[dep[a[i]]]=1;
}
cout<<"Yes\n";
togo:;
for(int i=1;i<=n;i++){
deg[i]=dep[i]=f[i]=g[i]=0;
e[i].clear();
}
}
return 0;
}
}
int main(){return asbt::main();}
B. 异或
区间操作不好处理,考虑令 \(d_i=a_i\oplus a_{i-1}\),于是一次区间操作变为单点操作或双点操作,目标仍为使数组归零。将每次操作的两点连边,答案即为总边数最小值。考虑一个大小为 \(x\) 的连通块,发现其边数最大为 \(x\)(基环树显然成立),最小为 \(x-1\)(树)。取得最小值的充要条件是该连通块异或和为零,证明较为简单。于是我们希望最大化这样的连通块个数,设其为 \(m\),答案即为 \(n-m\)。状压 DP 即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define popcnt __builtin_popcount
using namespace std;
namespace asbt{
const int maxn=(1<<17)+5;
int n,dp[maxn];
ll a[20],sum[maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=n;i;i--){
a[i]^=a[i-1];
}
for(int S=0;S<1<<n;S++){
for(int i=1;i<=n;i++){
if(S>>(i-1)&1){
sum[S]^=a[i];
}
}
}
int U=(1<<n)-1;
for(int S=0;S<1<<n;S++){
int nS=U^S;
for(int T=nS;T;T=(T-1)&nS){
if(!sum[T]){
dp[S|T]=max(dp[S|T],dp[S]+1);
}
}
}
cout<<n-dp[U];
return 0;
}
}
int main(){return asbt::main();}
C. 距离
首先考虑特殊性质 A,即每次只插入/查询一个点,可以用点分树解决,因为有 \(w\ge 1\) 所以可以直接点分树。
当引入点对时,我们离线下来,再套一层点分治即可。具体地,设当前的分治中心为 \(u\),对于修改操作 \((a,b)\),在点分树上的每个点 \(v\) 维护 \(val_v=\min\{\operatorname{dis}(a,u)+\operatorname{dis}(b,v)\}\)。那么对于查询 \((x,y)\),我们只需要求出 \(\min\{\operatorname{dis}(x,u)+val_v+\operatorname{dis}(y,v)\}\),更新答案即可。时间复杂度 \(O(n\log^2n)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
#define pii pair<int,int>
#define fir first
#define sec second
#define mp make_pair
using namespace std;
namespace asbt{
const int maxn=2e5+5;
const ll inf=1e18;
int n,m,rt,tot,fa[maxn],sz[maxn],mxs[maxn];
ll ans[maxn],cun[maxn];
bool ban[maxn];
vector<int> E[maxn],Q[maxn];
vector<pii> e[maxn];
struct{
int opt,a,b;
}q[maxn];
namespace LCA{
int cnt,dfn[maxn],oula[maxn<<1],idx[maxn<<1];
ll dep[maxn];
il void dfs(int u,int fa){
dfn[u]=++cnt;
oula[cnt]=cnt,idx[cnt]=u;
for(pii i:e[u]){
int v=i.fir,w=i.sec;
if(v==fa){
continue;
}
dep[v]=dep[u]+w;
dfs(v,u);
oula[++cnt]=dfn[u];
}
}
struct{
int st[20][maxn<<1],Log[maxn<<1];
il void build(){
for(int i=2;i<=cnt;i++){
Log[i]=Log[i>>1]+1;
}
for(int i=1;i<=cnt;i++){
st[0][i]=oula[i];
}
for(int j=1;j<=Log[cnt];j++){
for(int i=1;i+(1<<j)-1<=cnt;i++){
st[j][i]=min(st[j-1][i],st[j-1][i+(1<<(j-1))]);
}
}
}
il int query(int l,int r){
int p=Log[r-l+1];
return min(st[p][l],st[p][r-(1<<p)+1]);
}
}ST;
il void init(){
dfs(1,0),ST.build();
}
il int lca(int u,int v){
if(dfn[u]>dfn[v]){
swap(u,v);
}
return idx[ST.query(dfn[u],dfn[v])];
}
il ll dis(int u,int v){
return dep[u]+dep[v]-2*dep[lca(u,v)];
}
}
using LCA::dis;
il void dfs1(int u,int fa){
tot++;
for(pii i:e[u]){
int v=i.fir;
if(v==fa||ban[v]){
continue;
}
dfs1(v,u);
}
}
il int dfs2(int u,int fa){
sz[u]=1,mxs[u]=0;
int mnp=0;
ll mns=inf;
for(pii i:e[u]){
int v=i.fir;
if(v==fa||ban[v]){
continue;
}
int t=dfs2(v,u);
if(mxs[t]<mns){
mns=mxs[t],mnp=t;
}
sz[u]+=sz[v];
mxs[u]=max(mxs[u],sz[v]);
}
mxs[u]=max(mxs[u],tot-sz[u]);
return mns<mxs[u]?mnp:u;
}
il int build(int u){
// cout<<u<<" ";
tot=0,dfs1(u,0);
// cout<<tot<<"\n";
int x=dfs2(u,0);
ban[x]=1;
for(pii i:e[x]){
int v=i.fir;
if(ban[v]){
continue;
}
int y=build(v);
fa[y]=x,E[x].pb(y);
}
return x;
}
il void solve(int u){
// cout<<u<<":\n";
for(int i:Q[u]){
// cout<<i<<" ";
int opt=q[i].opt,a=q[i].a,b=q[i].b;
if(opt==1){
int x=b;
while(x){
cun[x]=min(cun[x],dis(x,b)+dis(a,u));
x=fa[x];
}
}
else{
int x=b;
while(x){
ans[i]=min(ans[i],dis(a,u)+cun[x]+dis(b,x));
x=fa[x];
}
}
}
// cout<<"\n";
for(int i:Q[u]){
int opt=q[i].opt,b=q[i].b;
if(opt==1){
int x=b;
while(x){
cun[x]=inf,x=fa[x];
}
}
}
for(int v:E[u]){
solve(v);
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1,u,v,w;i<n;i++){
cin>>u>>v>>w;
e[u].pb(mp(v,w));
e[v].pb(mp(u,w));
}
LCA::init();
// for(int u=1;u<=n;u++){
// for(int v=1;v<=n;v++){
// cout<<u<<" "<<v<<" "<<dis(u,v)<<"\n";
// }
// }
rt=build(1);
// cout<<rt<<"\n";
// for(int u=1;u<=n;u++){
// for(int v:E[u]){
// cout<<u<<" "<<v<<"\n";
// }
// }
for(int i=1;i<=m;i++){
cin>>q[i].opt>>q[i].a>>q[i].b;
int u=q[i].a;
while(u){
Q[u].pb(i);
u=fa[u];
}
}
memset(cun,0x3f,sizeof(cun));
memset(ans,0x3f,sizeof(ans));
solve(rt);
for(int i=1;i<=m;i++){
if(q[i].opt==2){
cout<<(ans[i]>=inf?-1:ans[i])<<"\n";
}
}
return 0;
}
}
int main(){return asbt::main();}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号