【比赛记录】2025CSP-S模拟赛15
| A | B | C | D | Sum | Rank |
|---|---|---|---|---|---|
| 50 | 20 | 60 | 8 | 138 | 10/21 |
A. 万花筒
对于一条边,假设 \(u<v\),则会连出 \(\gcd(n,v-u)\) 个环。于是按照 kruskal 的思路,每一个环留一条边不取即可。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
#define gcd __gcd
using namespace std;
namespace asbt{
const int maxn=1e5+5;
int T,n,m;
struct node{
int u,v,w;
node(int u=0,int v=0,int w=0):u(u),v(v),w(w){}
il bool operator<(const node &x)const{
return w<x.w;
}
}e[maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>n>>m;
for(int i=1,u,v,w;i<=m;i++){
cin>>u>>v>>w;
if(u>v){
swap(u,v);
}
e[i]=node(u,v,w);
}
sort(e+1,e+m+1);
int ans=0;
for(int i=1;i<=m;i++){
int d=e[i].v-e[i].u;
int t=gcd(n,d);
ans+=e[i].w*(n-t);
n=t;
}
cout<<ans<<"\n";
}
return 0;
}
}
signed main(){return asbt::main();}
B. 冒泡排序趟数期望
记每一个位置 \(i\) 前比 \(p_i\) 大的有 \(num_i\) 个,那么 \(res=\max_{i=1}^{n}num_i\)。又不难发现对于每个合法的 \(num\),都有一个唯一的 \(p\) 与之对应。于是可以枚举 \(k\),计算有多少个排列的 \(\max\{num_i\}=k\)。前 \(k\) 位可以乱选,后面的最大值一定为 \(k\),所以 \(k\) 的答案即为 \(k![(k+1)^{n-k}-k^{n-k}]\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e6+5,mod=1e9+7;
int n,fac[maxn];
il int qpow(int x,int y=mod-2){
int res=1;
while(y){
if(y&1){
res=res*1ll*x%mod;
}
x=x*1ll*x%mod,y>>=1;
}
return res;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
fac[0]=1;
for(int i=1;i<=n;i++){
fac[i]=fac[i-1]*1ll*i%mod;
}
int ans=0;
for(int i=0;i<n;i++){
(ans+=i*1ll*fac[i]%mod*(qpow(i+1,n-i)-qpow(i,n-i)+mod)%mod)%=mod;
}
cout<<ans*1ll*qpow(fac[n])%mod;
return 0;
}
}
int main(){return asbt::main();}
C. 数点
首先可以将点数的 \(k\) 次方拆成 \(j\le k\) 个点的贡献的线性和。具体地,对于 \(k=2\),\((a+b)^2=a^2+2ab+b^2\),于是一个点会有 \(1\) 的贡献,两个点会有 \(2\) 的贡献。\(k=3\) 是类似的。
我们分别考虑 \(j=1,2,3\) 的情况。对于 \(j=1\),\((i,p_i)\) 的贡献(即包含它的矩形数量)为 \(i\cdot p_i\cdot (n-i+1)\cdot (n-p_i+1)\)。这可以线性求出。
\(j=2\),设 \(x<y\land p_x<p_y\),贡献为 \(x\cdot p_x\cdot (n-y+1)\cdot (n-p_y+1)\)。于是可以扫描线,将 \(x\cdot p_x\) 插入树状数组,在 \(y\) 查询。对于 \(p_x>p_y\) 将数组倒过来再扫一遍即可。
\(j=3\),分布有 \(6\) 中情况,等价下来就两种:
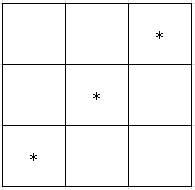
枚举中间那个点正着扫一遍再倒着扫一遍,类似的用树状数组即可。
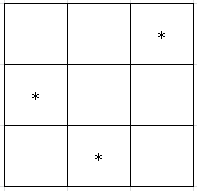
容易发现第一个点贡献左边界,第二个点贡献下边界。用线段树维护 \(\texttt{左}\times\texttt{下}\)。于是在第一个点,我们在 \(p_i\) 处给左加上 \(i\) 的贡献;在第二个点,我们给 \([p_i+1,n]\) 的下全都加上 \(p_i\) 的贡献;在第三个点进行区间查询即可。注意下只能从右边贡献,不能来自左侧。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
#define lid id<<1
#define rid id<<1|1
using namespace std;
namespace asbt{
const int maxn=1e5+5,mod=998244353;
int n,m,p[maxn],hp[maxn];
struct{
int tr[maxn];
il void init(){
memset(tr,0,sizeof(tr));
}
il int lowbit(int x){
return x&-x;
}
il void add(int p,int v){
for(;p<=n;p+=lowbit(p)){
(tr[p]+=v)%=mod;
}
}
il int query(int p){
int res=0;
for(;p;p-=lowbit(p)){
(res+=tr[p])%=mod;
}
return res;
}
}F;
struct node{
int a,sum;
node(int a=0,int sum=0):a(a),sum(sum){}
il node operator+(const node &x)const{
return node((a+x.a)%mod,(sum+x.sum)%mod);
}
};
struct{
int tag[maxn<<2];
node tr[maxn<<2];
il void pushup(int id){
tr[id]=tr[lid]+tr[rid];
}
il void pushtag(int id,int v){
(tag[id]+=v)%=mod;
(tr[id].sum+=tr[id].a*v)%=mod;
}
il void pushdown(int id){
if(tag[id]){
pushtag(lid,tag[id]);
pushtag(rid,tag[id]);
tag[id]=0;
}
}
il void build(int id,int l,int r){
tr[id]=node(),tag[id]=0;
if(l==r){
return ;
}
int mid=(l+r)>>1;
build(lid,l,mid);
build(rid,mid+1,r);
}
il void add(int id,int l,int r,int p,int v){
if(l==r){
(tr[id].a+=v)%=mod;
tr[id].sum=tag[id]=0;
return ;
}
pushdown(id);
int mid=(l+r)>>1;
if(p<=mid){
add(lid,l,mid,p,v);
}
else{
add(rid,mid+1,r,p,v);
}
pushup(id);
}
il void mul(int id,int L,int R,int l,int r,int v){
if(l>r){
return ;
}
if(L>=l&&R<=r){
pushtag(id,v);
return ;
}
pushdown(id);
int mid=(L+R)>>1;
if(l<=mid){
mul(lid,L,mid,l,r,v);
}
if(r>mid){
mul(rid,mid+1,R,l,r,v);
}
pushup(id);
}
il int query(int id,int L,int R,int l,int r){
if(L>=l&&R<=r){
return tr[id].sum;
}
pushdown(id);
int mid=(L+R)>>1,res=0;
if(l<=mid){
(res+=query(lid,L,mid,l,r))%=mod;
}
if(r>mid){
(res+=query(rid,mid+1,R,l,r))%=mod;
}
return res;
}
}S;
il int calc1(){
int res=0;
for(int i=1;i<=n;i++){
(res+=i*p[i]*(n-i+1)%mod*(n-p[i]+1))%=mod;
}
return res;
}
il int calc2(){
int res=0;
F.init();
for(int i=1;i<=n;i++){
(res+=(n-i+1)*(n-p[i]+1)%mod*F.query(p[i]))%=mod;
F.add(p[i],i*p[i]%mod);
}
reverse(p+1,p+n+1);
F.init();
for(int i=1;i<=n;i++){
(res+=(n-i+1)*(n-p[i]+1)%mod*F.query(p[i]))%=mod;
F.add(p[i],i*p[i]%mod);
}
return res;
}
il int calc3(){
int res=0;
F.init();
for(int i=1;i<=n;i++){
hp[i]=F.query(p[i]);
F.add(p[i],i*p[i]%mod);
}
F.init();
for(int i=n;i;i--){
(res+=hp[i]*(F.query(n)-F.query(p[i])+mod))%=mod;
F.add(p[i],(n-i+1)*(n-p[i]+1)%mod);
}
reverse(p+1,p+n+1);
F.init();
for(int i=1;i<=n;i++){
hp[i]=F.query(p[i]);
F.add(p[i],i*p[i]%mod);
}
F.init();
for(int i=n;i;i--){
(res+=hp[i]*(F.query(n)-F.query(p[i])+mod))%=mod;
F.add(p[i],(n-i+1)*(n-p[i]+1)%mod);
}
S.build(1,1,n);
for(int i=1;i<=n;i++){
(res+=(n-i+1)*(n-p[i]+1)%mod*S.query(1,1,n,1,p[i]))%=mod;
S.add(1,1,n,p[i],i);
S.mul(1,1,n,p[i]+1,n,p[i]);
}
reverse(p+1,p+n+1);
S.build(1,1,n);
for(int i=1;i<=n;i++){
(res+=(n-i+1)*(n-p[i]+1)%mod*S.query(1,1,n,1,p[i]))%=mod;
S.add(1,1,n,p[i],i);
S.mul(1,1,n,p[i]+1,n,p[i]);
}
for(int i=1;i<=n;i++){
p[i]=n-p[i]+1;
}
S.build(1,1,n);
for(int i=1;i<=n;i++){
(res+=(n-i+1)*(n-p[i]+1)%mod*S.query(1,1,n,1,p[i]))%=mod;
S.add(1,1,n,p[i],i);
S.mul(1,1,n,p[i]+1,n,p[i]);
}
reverse(p+1,p+n+1);
S.build(1,1,n);
for(int i=1;i<=n;i++){
(res+=(n-i+1)*(n-p[i]+1)%mod*S.query(1,1,n,1,p[i]))%=mod;
S.add(1,1,n,p[i],i);
S.mul(1,1,n,p[i]+1,n,p[i]);
}
return res;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>p[i];
}
int ans=0;
switch(m){
case 1:{
ans=calc1();
break;
}
case 2:{
ans=(calc1()+2*calc2())%mod;
break;
}
default:{
ans=(calc1()+6*calc2()+6*calc3())%mod;
break;
}
}
cout<<ans;
return 0;
}
}
signed main(){return asbt::main();}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号