【学习笔记】笛卡尔树
前言
本来早就该学笛卡尔树了,但暑假打模拟赛就一直没学成。于是就打算先不学了,结果又发现后面有个笛卡尔树专题,只好来学学。
定义
笛卡尔树是一棵二叉树,每个点有一个键和一个值,键满足堆的性质,值满足二叉搜索树的性质。没错当键随机时,这就是个 Treap。
建树
如果值单调递增,那么就可以线性建树。具体地,维护整棵树的右链。右链就是从根开始不停往右儿子走的链。因为值递增所以新加的点一定会在右链中。假设新加入的点 \(u\) 值为 \(k\) 键为 \(w\),记为 \((k,w)\),则从右链下端开始不断向上比较,找到一个 \(x\) 使它的键小于 \(w\)。那么 \(u\) 就成为 \(x\) 的右儿子,\(x\) 原本的右儿子就成为 \(u\) 的左儿子。
放张图更直观(红色方框即为右链):
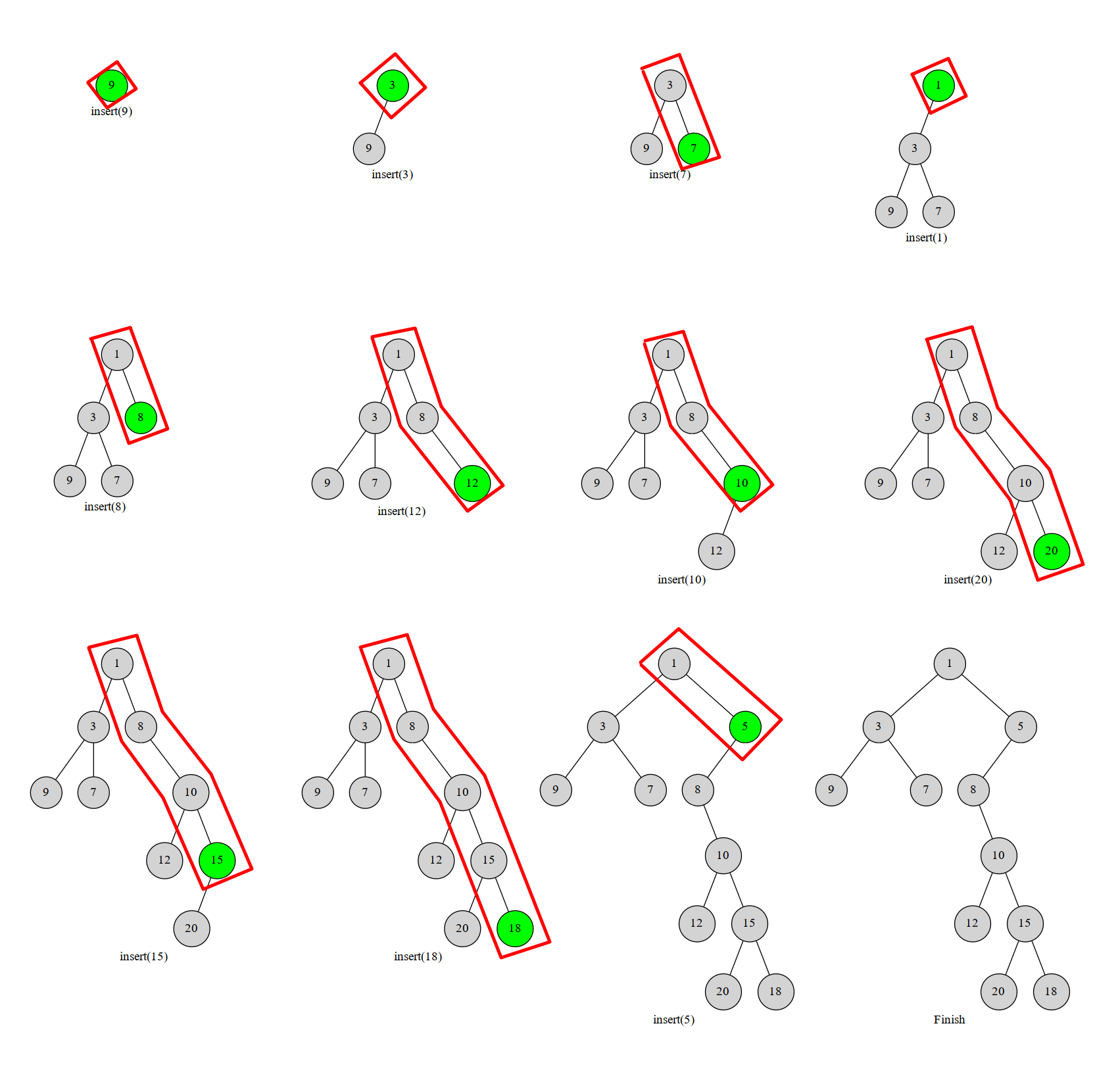
图中的数字就是相应的点的键。显然用单调栈来维护右链就行了。
核心代码:
for(int i=1;i<=n;i++){
while(top&&a[zhan[top]]>a[i]){
top--;
}
int &tmp=top?rs[zhan[top]]:rt;
ls[i]=tmp;
tmp=i;
zhan[++top]=i;
}
代码中值为 \(i=1\dots n\),对应的键为 \(a_i\)。
例题
[luogu5854]笛卡尔树模板
按如上方式建树即可。值得一提的是通过这道题可以发现:当键与值都互不相同时,笛卡尔树的形态是唯一的。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define read(x){\
char ch;\
int fu=1;\
while(!isdigit(ch=getchar()))\
fu-=(ch=='-')<<1;\
x=ch&15;\
while(isdigit(ch=getchar()))\
x=(x<<1)+(x<<3)+(ch&15);\
x*=fu;\
}
using namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=1e7+5;
int n,a[maxn],rt;
int zhan[maxn],top;
int ls[maxn],rs[maxn];
namespace cplx{
bool end;
il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){
read(n);
for(int i=1;i<=n;i++){
read(a[i]);
}
for(int i=1;i<=n;i++){
while(top&&a[zhan[top]]>a[i]){
top--;
}
int &tmp=top?rs[zhan[top]]:rt;
ls[i]=tmp;
tmp=i;
zhan[++top]=i;
}
ll ans1=0,ans2=0;
for(int i=1;i<=n;i++){
ans1^=i*1ll*(ls[i]+1);
ans2^=i*1ll*(rs[i]+1);
}
printf("%lld %lld",ans1,ans2);
return 0;
}
}
int main(){return asbt::main();}
[TJOI2011] 树的序
观察原树的建树方式,发现先加的一定在后加的上面。换句话说对于题中给出的 \(k_i\),下标 \(i\) 为键而 \(k_i\) 为值。因此先将 \(k\) 排序,用笛卡尔树的方式线性建树。
然后我们要找到能建出相同树的序列,必然也是从上向下建的,而我们又想要字典序最小,这还是一棵二叉搜索树,因此必然要先输出根,再遍历左子树,然后再遍历右子树。一个 dfs 即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define read(x){\
char ch;\
int fu=1;\
while(!isdigit(ch=getchar()))\
fu-=(ch=='-')<<1;\
x=ch&15;\
while(isdigit(ch=getchar()))\
x=(x<<1)+(x<<3)+(ch&15);\
x*=fu;\
}
using namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=1e5+5;
int n,a[maxn],p[maxn];
int rt,ls[maxn],rs[maxn];
int top,zhan[maxn];
il void dfs(int u){
if(!u){
return ;
}
printf("%d ",u);
dfs(ls[u]);
dfs(rs[u]);
}
namespace cplx{
bool end;
il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){
read(n);
for(int i=1;i<=n;i++){
read(a[i]);
p[i]=i;
}
sort(p+1,p+n+1,[](const int &x,const int &y){return a[x]<a[y];});
for(int i=1;i<=n;i++){
// cout<<p[i]<<"\n";
while(top&&p[zhan[top]]>p[i]){
top--;
}
int &tmp=top?rs[zhan[top]]:rt;
ls[i]=tmp;
tmp=i;
zhan[++top]=i;
}
// for(int i=1;i<=n;i++){
// cout<<i<<" "<<ls[i]<<" "<<rs[i]<<"\n";
// }
dfs(rt);
return 0;
}
}
int main(){return asbt::main();}
[hdu6305]RMQ Similar Sequence
首先,对 \(A\) 数组建一个满足大根堆性质的笛卡尔树。
这时候你发现,\(RMQ(A,l,r)\) 就是 \(l\) 和 \(r\) 的 \(lca\)。
因此如果也类似地给 \(B\) 建出笛卡尔树,这两棵树一定是相同的。因为 \(B\) 的和的期望是确定的,即 \(\frac{n}{2}\),因此只需计算一个笛卡尔树与 \(A\) 的笛卡尔树相同的概率就行了。
显然对于每棵子树,只要根都是相同的,则树就一定是相同的。设 \(sz\) 为子树大小,则概率为 \(\frac{1}{\prod{sz_i}}\)。因此答案为\(\frac{n}{2\prod{sz_i}}\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define read(x){\
char ch;\
int fu=1;\
while(!isdigit(ch=getchar()))\
fu-=(ch=='-')<<1;\
x=ch&15;\
while(isdigit(ch=getchar()))\
x=(x<<1)+(x<<3)+(ch&15);\
x*=fu;\
}
using namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=1e6+5,mod=1e9+7;
int T,n,a[maxn],rt;
int zhan[maxn],top;
int ls[maxn],rs[maxn];
int inv[maxn],sz[maxn];
il void dfs(int u){
// cout<<u<<"\n";
if(!u){
return ;
}
dfs(ls[u]);
dfs(rs[u]);
sz[u]=sz[ls[u]]+sz[rs[u]]+1;
}
namespace cplx{
bool end;
il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){
inv[1]=1;
for(int i=2;i<=1e6;i++){
inv[i]=(mod-mod/i)*1ll*inv[mod%i]%mod;
}
// for(int i=1;i<=1e6;i++){
// cout<<i*1ll*inv[i]%mod<<"\n";
// }
read(T);
while(T--){
read(n);
top=rt=0;
for(int i=1;i<=n;i++){
read(a[i]);
while(top&&a[zhan[top]]<a[i]){
top--;
}
int &tmp=top?rs[zhan[top]]:rt;
ls[i]=tmp;
tmp=i;
zhan[++top]=i;
}
dfs(rt);
int ans=inv[2]*1ll*n%mod;
for(int i=1;i<=n;i++){
ans=ans*1ll*inv[sz[i]]%mod;
}
printf("%d\n",ans);
for(int i=1;i<=n;i++){
ls[i]=rs[i]=sz[i]=0;
}
}
return 0;
}
}
int main(){return asbt::main();}
[洛谷 P6453]PERIODNI
考虑如果 \(a_i\) 很小,那 \(i\) 两边的高于 \(a_i\) 的部分就成了两个独立的子问题。因此可以建立小根堆笛卡尔树,然后进行树形 DP。
设 \(f_{u,i}\) 表示 \(u\) 的子树中高于 \(a_{fa_u}\) 的地方放了 \(i\) 个点的方案数。显然答案为 \(f_{rt,m}\)。
考虑转移。首先是高于 \(a_u\) 的部分,显然可以通过树上背包转移:
然后是 \((a_{fa_u},a_u]\) 的部分。设要放 \(i\) 个,有 \(j\) 个在 \((a_{fa_u},a_u]\),剩下大于 \(a_u\),即要在剩下 \(sz_u-(i-j)\) 个节点、\(a_u-a_{fa_u}\) 个高度中选择 \(j\) 个位置放点。于是有转移方程:
注意两次转移中都是小的更新大的,所以 \(i\) 要倒序遍历。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define read(x){\
char ch;\
int fu=1;\
while(!isdigit(ch=getchar()))\
fu-=(ch=='-')<<1;\
x=ch&15;\
while(isdigit(ch=getchar()))\
x=(x<<1)+(x<<3)+(ch&15);\
x*=fu;\
}
using namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=505,mod=1e9+7,maxm=1e6+5;
int n,m,a[maxn],sz[maxn];
int rt,top,zhan[maxn];
int ls[maxn],rs[maxn];
int f[maxn][maxn];
int fac[maxm],inv[maxm];
il int qpow(int x,int y){
int res=1;
while(y){
if(y&1){
res=res*1ll*x%mod;
}
x=x*1ll*x%mod,y>>=1;
}
return res;
}
il void init(int x){
fac[0]=1;
for(int i=1;i<=x;i++){
fac[i]=fac[i-1]*1ll*i%mod;
}
inv[x]=qpow(fac[x],mod-2);
for(int i=x;i;i--){
inv[i-1]=inv[i]*1ll*i%mod;
}
}
il int C(int x,int y){
if(x<y||y<0){
return 0;
}
return fac[x]*1ll*inv[y]%mod*inv[x-y]%mod;
}
il int A(int x,int y){
if(x<y||y<0){
return 0;
}
return fac[x]*1ll*inv[x-y]%mod;
}
il void dfs(int u,int fa){
if(!u){
return ;
}
dfs(ls[u],u),dfs(rs[u],u);
sz[u]=sz[ls[u]]+sz[rs[u]]+1;
f[u][0]=1;
for(int i=min(m,sz[u]);i;i--){
for(int j=1;j<=min(i,sz[ls[u]]);j++){
f[u][i]=(f[u][i]+f[u][i-j]*1ll*f[ls[u]][j])%mod;
}
}
for(int i=min(m,sz[u]);i;i--){
for(int j=1;j<=min(i,sz[rs[u]]);j++){
f[u][i]=(f[u][i]+f[u][i-j]*1ll*f[rs[u]][j])%mod;
}
}
for(int i=min(m,sz[u]);i;i--){
for(int j=1;j<=i;j++){
f[u][i]=(f[u][i]+f[u][i-j]*1ll*C(a[u]-a[fa],j)%mod*A(sz[u]-i+j,j))%mod;
}
}
}
namespace cplx{
bool end;
il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){
read(n)read(m);
for(int i=1;i<=n;i++){
read(a[i]);
while(top&&a[zhan[top]]>a[i]){
top--;
}
int &tmp=top?rs[zhan[top]]:rt;
ls[i]=tmp;
tmp=zhan[++top]=i;
}
init(1e6);
dfs(rt,0);
printf("%d",f[rt][m]);
return 0;
}
}
int main(){return asbt::main();}
[hdu4125]Moles
显然我们找到原树模 \(2\) 意义下的欧拉序,跑一个 kmp 就好了。
考虑如何建树,这棵树按 \(a\) 值满足二叉搜索树的性质,按下标满足小根堆的性质。所以这就是一棵笛卡尔树。线性建树即可。时间复杂度 \(O(n\log n)\)。
Code
#include<cstdio>
#include<ctype.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#define ll long long
#define il inline
#define read(x){\
char ch;\
int fu=1;\
while(!isdigit(ch=getchar()))\
fu-=(ch=='-')<<1;\
x=ch&15;\
while(isdigit(ch=getchar()))\
x=(x<<1)+(x<<3)+(ch&15);\
x*=fu;\
}
using namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=6e5+5;
int T,n,zhan[maxn],nxt[maxn];
int a[maxn],p[maxn],tot;
int ls[maxn],rs[maxn];
char s[maxn],t[maxn<<1];
il void dfs(int u){
t[++tot]=u&1|48;
if(ls[u]){
dfs(ls[u]);
t[++tot]=u&1|48;
}
if(rs[u]){
dfs(rs[u]);
t[++tot]=u&1|48;
}
}
il void solve(){
read(n);
for(int i=1;i<=n;i++){
read(a[i]);
p[i]=i;
}
scanf(" %s",s+1);
int len=strlen(s+1);
int top=0,rt=0;
sort(p+1,p+n+1,[](const int &x,const int &y){return a[x]<a[y];});
for(int i=1;i<=n;i++){
while(top&&p[zhan[top]]>p[i]){
top--;
}
int &tmp=top?rs[zhan[top]]:rt;
ls[i]=tmp;
tmp=zhan[++top]=i;
}
tot=0;
dfs(rt);
// for(int i=1;i<=tot;i++){
// cout<<t[i];
// }
// puts("");
nxt[1]=0;
for(int i=2,j=0;i<=len;i++){
while(j&&s[j+1]!=s[i]){
j=nxt[j];
}
if(s[j+1]==s[i]){
j++;
}
nxt[i]=j;
}
int ans=0;
for(int i=1,j=0;i<=tot;i++){
while(j&&s[j+1]!=t[i]){
j=nxt[j];
}
if(s[j+1]==t[i]){
j++;
}
if(j==len){
ans++,j=nxt[j];
}
}
printf("%d\n",ans);
for(int i=1;i<=n;i++){
ls[i]=rs[i]=0;
}
}
namespace cplx{
bool end;
il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){
// cout<<cplx::usdmem();
read(T);
for(int i=1;i<=T;i++){
printf("Case #%d: ",i);
solve();
}
return 0;
}
}
int main(){return asbt::main();}
[hdu6854]Kcats
考虑 \(a\) 的实际含义,即为 \(p\) 的小根笛卡尔树上 \(i\) 到根上权值 \(\le\) 的点数。于是可以进行区间 dp。设 \(f_{i,j,x}\) 表示 \([i,j]\) 的根的 \(a\) 值为 \(x\) 的方案数。于是有转移:
时间复杂度是 \(O(Tn^4)\) 的,但是能过。
Code
#include<cstdio>
#include<iostream>
#include<functional>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
int main(){
ios::sync_with_stdio(0),cin.tie(0);
const int mod=1e9+7;
function<int(int,int)>qpow=[](int x,int y)->int{
int res=1;
while(y){
if(y&1){
res=res*1ll*x%mod;
}
y>>=1,x=x*1ll*x%mod;
}
return res;
};
int *fac=new int[105](),*inv=new int[105]();
fac[0]=1;
for(int i=1;i<=100;i++){
fac[i]=fac[i-1]*1ll*i%mod;
}
inv[100]=qpow(fac[100],mod-2);
for(int i=100;i;i--){
inv[i-1]=inv[i]*1ll*i%mod;
}
// for(int i=0;i<=100;i++){
// cout<<fac[i]<<" "<<fac[i]*1ll*inv[i]%mod<<"\n";
// }
function<int(int,int)>C=[=](int x,int y)->int{
if(x<y||y<0){
return 0;
}
return fac[x]*1ll*inv[y]%mod*inv[x-y]%mod;
};
int *a=new int[105]();
int (*f)[105][105]=new int[105][105][105]();
int T;
cin>>T;
while(T--){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
f[i][j][k]=0;
}
}
}
for(int len=1;len<=n;len++){
for(int i=1,j=len;j<=n;i++,j++){
for(int k=i,l,r;k<=j;k++){
if(~a[k]){
l=r=a[k];
}
else{
l=1,r=n;
}
for(int x=l;x<=r;x++){
(f[i][j][x]+=C(j-i,k-i)*1ll*(i<k?f[i][k-1][x]:1)%mod*(k<j?f[k+1][j][x+1]:1)%mod)%=mod;
}
}
}
}
cout<<f[1][n][1]<<"\n";
}
delete[] fac,inv,a,f;
return 0;
}
}
int main(){return asbt::main();}
啊上面这个因为 hdu 评测机太慢过不了,这告诉我们可以用杨辉三角时就用吧,还有不要用 new 定义数组。。。
Code
#include<cstdio>
#include<iostream>
#include<functional>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int mod=1e9+7;
int C[105][105],a[105],f[105][105][105];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
for(int i=0;i<=100;i++){
C[i][0]=1;
for(int j=1;j<=i;j++){
C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
}
int T;
cin>>T;
while(T--){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
f[i][j][k]=0;
}
}
}
for(int len=1;len<=n;len++){
for(int i=1,j=len;j<=n;i++,j++){
for(int k=i,l,r;k<=j;k++){
if(~a[k]){
l=r=a[k];
}
else{
l=1,r=n;
}
for(int x=l;x<=r;x++){
(f[i][j][x]+=C[j-i][k-i]*1ll*(i<k?f[i][k-1][x]:1)%mod*(k<j?f[k+1][j][x+1]:1)%mod)%=mod;
}
}
}
}
cout<<f[1][n][1]<<"\n";
}
return 0;
}
}
int main(){return asbt::main();}
复杂度看起来假的离谱的 dp 如果常数小有可能就是真的了……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号