求树上k级祖先

长链剖分

1.前言

在学习淀粉质的时候，看到了P4292 [WC2010]重建计划这道题，发现可以用长链剖分来做。就学一下。

2.定义

2.1长链

长链的概念和重链相似

点\(x\)的长链指的是从\(x\)出发，到达的子树中深度最深的儿子所经过的路径

2.2长儿子♂

\(x\)所在的长链上的儿子称之为长儿子♂

2.3长链剖分

和轻重链剖分类似，通过树上存在的长链，把一棵树分割成几条不相交的路径

就变成了这样

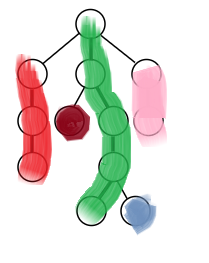
2.4顶点

意思是一条长链上深度最小的节点，也就是最顶上的那个点。

3.亿些性质

3.1

对树进行长链剖分之后所有的长链的长度的和为\(n\)

显然

3.2

任意一个点\(x\)的\(k\)级祖先\(y\)所在长链长度一定\(\geq k\)。

证明:

1. 若他们两个在同一条长链上

上面可能有一些，下面还可能有一点

显然成立

2. 若他们两个不在同一条长链上

考虑最接小的的情况

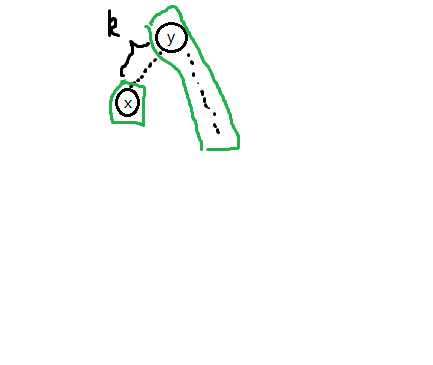
因为不在同一个长链上，所以\(y\)在的那一条长链的深度一定比\(x\)在的那条长链的深度\(+k\)要长

所以\(y\)在的那一条长链的长度\(\geq k\)。

3.3 : 3.2的应用

由于长链剖分根据深度大小进行剖分，因此可以解决一些与深度有关的问题。

3.3.1 \(O([1, n\log_2 n])\)时间在线问一个节点的\(k\)级祖先

传送门

预处理

1. 对树进行长剖，记录每个节点所在链的顶点和深度。\(O(n)\)
2. 树上倍增求出每个节点的\(2^n\)祖先，\(O(n\log_2 n)\)
3. 对于每条链，如果其长度为\(len\)，那么在顶点处记录顶点向上的\(len\)个祖先和向下的\(len\)个链上的儿子，\(O(n)\)
4. 对于\(i\in [1,n]\)求出二进制下的最高位\(h_i\)，\(O(n)\)

对于每一次询问\(x\)的\(k\)级祖先

1. 利用倍增跳到\(2^{h_k}\)级祖先，设剩下还有\(k'\)级，显然\(k' < 2^(h_k)\)，因此此时\(x\)所在的长链的长度\(len\geq 2^{h_k}>k'\)
2. 由于长链长度\(>k'\)，因此可以将\(x=top_x\)，若之后剩下的级数为正，就利用向上的数组来求答案，反之毅然

这样时间复杂度为\(O([1, n\log_2 n])\)了

Code

#include <bits/stdc++.h>
#define ll long long
#define ui unsigned int
using namespace std;
const int MAXN = 500010;
ui s;
inline ui get(ui x) 
{
	x ^= x << 13; x ^= x >> 17; x ^= x << 5; return s = x;
}
int n, q, fa[MAXN][32], g[MAXN]; //g[x] ---- log2 x
vector<int> nbr[MAXN];
int root, dep[MAXN], d[MAXN]; 
//dep[i]----max deep of node i      
//d[i]---node i's deep
int top[MAXN], son[MAXN];
vector<int> up[MAXN], dn[MAXN];
void Pre(int cur)
{
//	cout << cur;
	d[cur] = dep[cur] = d[fa[cur][0]] + 1;
	for(int i = 0; i < nbr[cur].size(); i ++)
	{
//		cout << i << ' ';
		int to = nbr[cur][i];
		fa[to][0] = cur;
		for(int j = 0; fa[to][j]; j ++) 
			fa[to][j + 1] = fa[fa[to][j]][j];
		Pre(to);
		if(dep[to] > dep[cur])
			dep[cur] = dep[to], son[cur] = to;
	}
	return ;
}
void Dfs(int cur, int p)
{
	top[cur] = p;
	if(cur == p)
	{
		for(int i = 0, tmp = cur; i < dep[cur] - d[cur]; i ++)
			up[cur].push_back(tmp), tmp = fa[tmp][0];
		for(int i = 0, tmp = cur; i < dep[cur] - d[cur]; i ++)
			dn[cur].push_back(tmp), tmp = son[tmp];
	}
	if(son[cur]) Dfs(son[cur], p);
	for(int i = 0; i < nbr[cur].size(); i ++)
	{
		int to = nbr[cur][i];
		if(to == son[cur]) continue;
		Dfs(to, to);
	}
	return ;
}
int ask(int x, int k) // x's  k-level father
{
	if(!k) return x;
	x = fa[x][g[k]]; 
	k -= 1 << g[k]; 
	k -= d[x] - d[top[x]];
	x = top[x];
	return k >= 0 ? up[x][k] : dn[x][-k];
}
int main()
{
	cin >> n >> q >> s;
	g[0] = -1;
	for(int i = 1; i <= n; i ++)
	{
		cin >> fa[i][0];
//		cout << "AE@#A@#@" << i << 'a' << endl;
		nbr[fa[i][0]].push_back(i);
		g[i] = g[i >> 1] + 1;
	}
//	cout << "ASDAW";
	root = nbr[0][0];
	Pre(root);
	Dfs(root, root);
//	cout << "&*^*$*(";
	Dfs(root, root);
	int lastans = 0, x = 0, k = 0;
	ll ans;
	for(int i = 1; i <= q; i ++)
	{
		x = (get(s) ^ lastans) % n + 1;
		k = (get(s) ^ lastans) % d[x];
		// cout << x << ' ' << k << ' ';
		ans ^= 1ll * i * (lastans = ask(x, k));
		// cout << lastans << endl;
	}
	cout << ans;
	return 0;
}

没了