Day8 应用机器学习的建议

决定下一步做什么

　　假设我们已经创建了一个用于预测房价的正则化的线性回归模型，但发现这个模型并不能很好的拟合新的样本，接下来我们就需要改进我们的模型，我们应该怎么做？

　　- 获取更多的训练集

　　- 尝试用较少的特征值来避免过拟合

　　- 尝试添加新的特征值

　　- 尝试在假设函数中用不同的特征值组合

　　- 尝试减小正规化参数λ

　　- 尝试增大正规化参数λ

　　以上的这些方法可能会有效，但也可能浪费大量时间而没有进展。

　　我们需要利用一些“机器学习诊断法”来帮我们弄清楚选择哪种方法可以改进我们的算法。

评估假设函数

　　假设在房价预测的过程中，我们有如下10个训练集：

　　

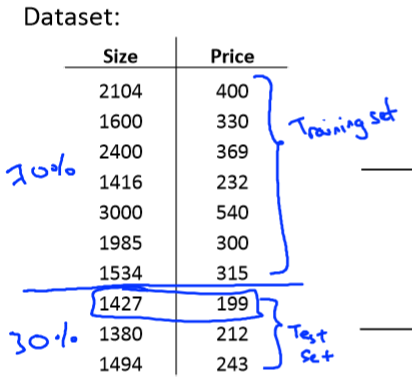
　　我们可以将其中的70%用来建立假设函数，剩余的30%用来进行测试。

　　若使用线性回归，我们首先需要利用70%的训练集得到参数θ，然后利用30%的测试集来计算测试误差：

　　

　　若使用逻辑回归，同样要先计算出θ，然后计算测试误差：

　　

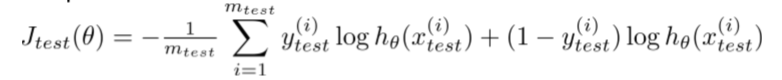
　　如果是二元分类问题，测试误差可以按以下方法计算：

　　0/1错分率：

　  　

模型选择和交叉验证

　　在房价预测问题中，我们需要选择一个多项式作为假设函数。

　　例如有以下10个多项式，我们需要从中找出最合适的一个。其中d表示多项式的次数。

　　

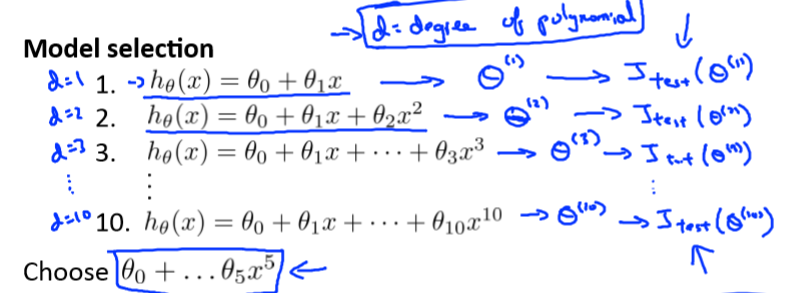
　　我们计算每一个多项式的测试误差，然后选取最小的。

　　但是适合于训练集的假设函数不一定就有很好的泛化性。

　　交叉验证

　　把训练集分为3部分：60%作为训练集，20%作为交叉验证集，20%作为测试集。

　　

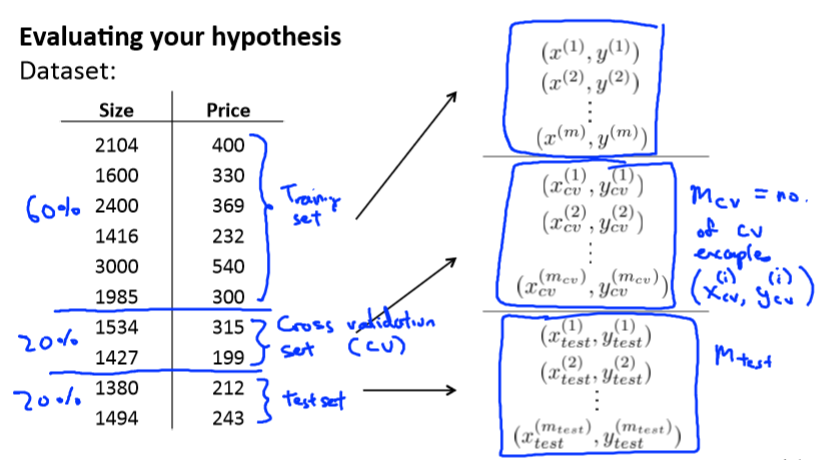
　　然后得到训练误差，交叉验证误差，测试误差：

　　

 　　最后得出模型选择的方法为：

　　　　1.利用训练集得出每个假设函数的θ；

　　　　2.找到有最小交叉验证误差的假设函数；

　　　　3.利用测试集来评估假设函数。

偏差和方差

　　当我们的假设函数拟合训练集时，可能会出现以下三种情况：

　　

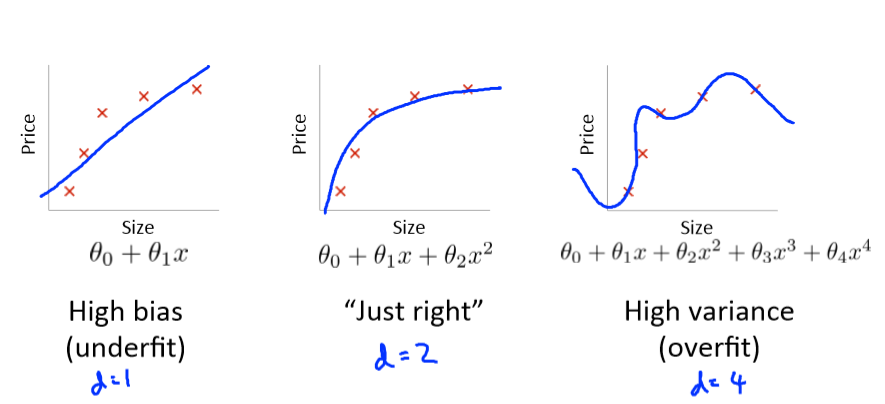
　　我们需要得出是由于高偏差（欠拟合）还是高方差（过拟合）导致我们的算法无法很好的进行预测。

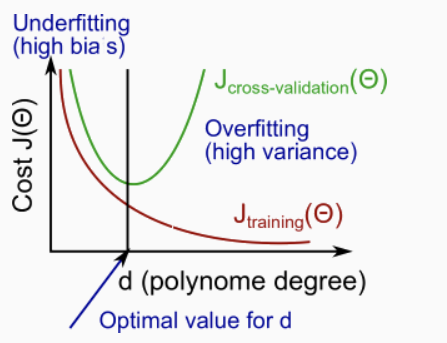
　　通过计算训练集误差和交叉验证误差，可以得到：

　　　　高偏差（欠拟合）：训练集误差和交叉验证误差都很高且训练集误差和交叉验证误差大致相等。

　　　　高方差（过拟合）：训练集误差很低，交叉验证误差比训练集误差高很多。

　　　　　　

正则化与偏差/方差

　　在正则化过程中，我们会遇到以下情况：

　　

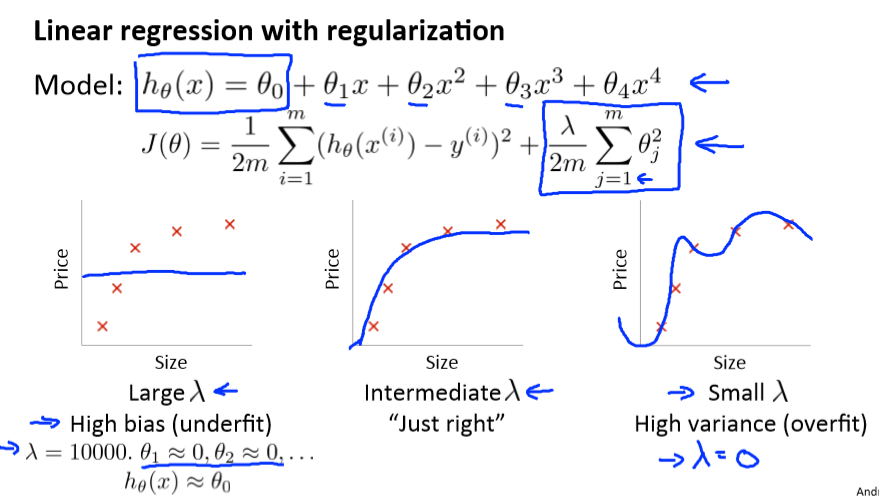
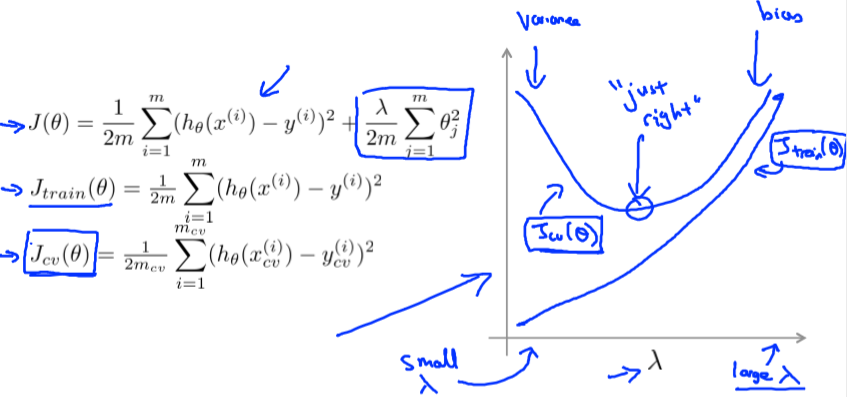
　　为了选择一个合适的参数λ，我们需要：

　　　　- 创建一个λ值的列表，如 λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24}

　　　　- 为每个λ值计算θ，并计算交叉验证误差

　　　　- 选择使交叉验证误差最小的λ。

　　

学习曲线Learning Curves

　　通过学习曲线，我们可以判断我们的算法是否处于高偏差或高方差还是两者都有。

　　学习曲线是训练集误差和交叉验证误差随着训练集增多而变化的曲线。

　　·

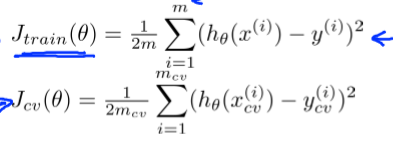
　　高偏差：

　　

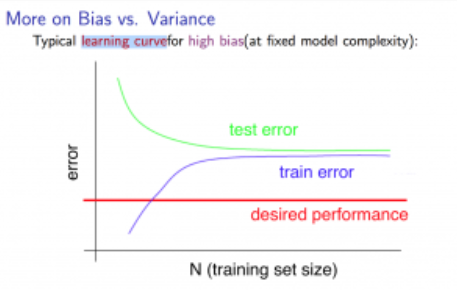
　　此时减少训练集的个数就没有什么用处。

　　高方差：

　　

　　此时增加训练集的个数就很有用。

总结

　　- 获取更多的训练集：                               修正高方差

　　- 尝试用较少的特征值来避免过拟合：      修正高方差

　　- 尝试添加新的特征值：                            修正高偏差

　　- 尝试在假设函数中用不同的特征值组合：修正高偏差

　　- 尝试减小正规化参数λ：                           修正高偏差

　　- 尝试增大正规化参数λ：                           修正高方差

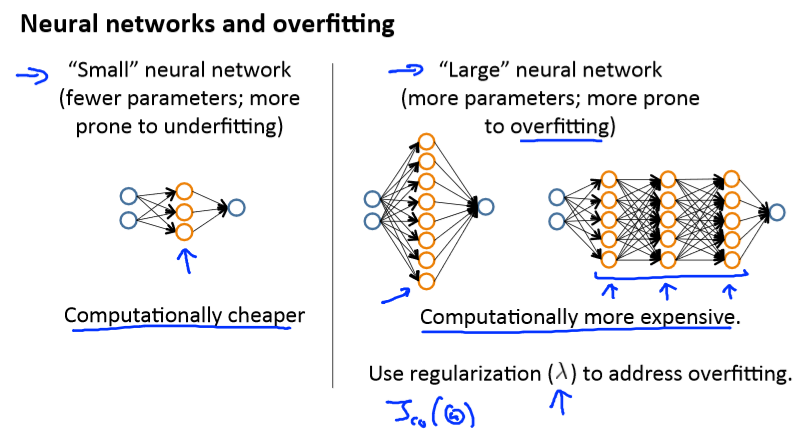
 　　在神经网络中，

　　如果使用较少的隐藏层，那么计算量小但容易出现欠拟合；

　　若使用较多隐藏层或隐藏层的单元较多，那么计算量大且 容易出现过拟合，此时可以用正则化加以修正。