最短路算法总结

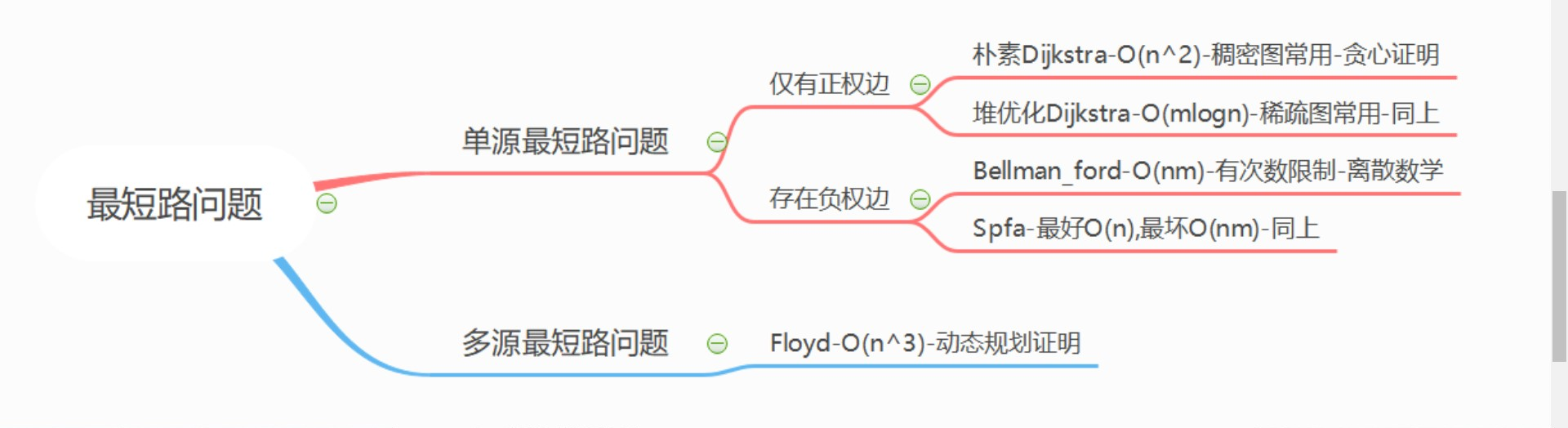
朴素版Dijkstra(适用于 无负权变的稠密图)

#include <iostream>
#include <cstring>

using namespace std;
const int N = 510;
int n, m;
int dis[N], g[N][N];  // dis数组存放起点到各点之间的最短距离
bool st[N];  // st数组判断这个点是否已经加入了最短路径的集合

int Dijkstra(int start, int end){
    memset(dis, 0x3f, sizeof dis);
    dis[start] = 0;  // 起点到起点的距离为0，同时不能吧st[起点]变成1， 不然不会更新与起点相邻的点
    for(int i = 0; i < n; ++i){
        int t = -1;
        // 在未加入最短路集合的点中找到距离起点最小的点
        for(int j = 1; j <= n; ++j){
            if(!st[j] && (t == -1 || dis[t] > dis[j]))
                t = j;
        }
        //将找到的点加入集合
            
        st[t] = true;

        // 由这个点来更新起点到其他点的距离
        for(int j = 1; j <= n; ++j){
            dis[j] = min(dis[j], dis[t] + g[t][j]);
        }
    }
    
    return dis[end];
}

int main(){
    memset(g, 0x3f, sizeof g);
    scanf("%d%d", &n, &m);
    
    while(m --){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);
    }
    
    int ans = Dijkstra(1, n);
    if(ans == 0x3f3f3f3f) printf("-1");
    else printf("%d", ans);
    return 0;
}

Bellman-Ford算法时间辅助度O(n*m) 几乎不会使用，除了少数情况如这题，要求最多k条边的最短路径，适用于稀疏图，可以处理负权边，同时可以判断是否存在负环，但是一般不用他来判断负环，用队列优化版的Bellman-Ford也就是spfa算法来判断负环。

#include <iostream>
#include <cstring>

using namespace std;
const int N = 10010, M = 510;
int dist[M], backup[M]; // backup 为dist的拷贝数组
// 对建边没有条件，所以直接用一个结构体数组来存储
struct Edge{
    int a, b, v;
}edges[N];
int n, m, k;

// 全名Bellman_ford算法，几乎不用，除了这道题，因为k表示的最多经过k条边的最短路径当
int bf(int start, int end){
    memset(dist, 0x3f, sizeof dist);
    dist[start] = 0;
    for(int i = 0; i < k; ++i){
        memcpy(backup, dist, sizeof dist);  // 为了让每次在下面for循环中dist不被反复更新，我们让backup为上一次循环的dist数组
        for(int j = 0; j < m; ++j){
            auto t = edges[j];
            dist[t.b] = min(dist[t.b], backup[t.a] + t.v);  // 用上一次的dist数组来更新
        }
    }
    return dist[end];
}

int main(){
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 0; i < m; ++i){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }
    
    int ans = bf(1, n);
    if(ans > 0x3f3f3f3f / 2) puts("impossible");  // 因为可能存在负权变所以正无穷的边也可能被更新
    else printf("%d", ans);
    return 0;
}

队列优化版Bellman-Ford也叫Spfa，适用于稀疏图，可处理负权边以及判断负环，时间复杂度O(m)，但有一种将时间复杂度卡到O(n*m)的方法这时就有可能超时，但一般不会卡

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;
const int N = 100010;
int h[N], ne[N], e[N], w[N], idx;
int n, m;
int dis[N], st[N];
queue<int> q;

// 链式前向星核心代码
void add(int a, int b, int c){
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa(int start){
    memset(dis, 0x3f, sizeof dis);  // 初始化
    q.push(start);  // 将起点放入队列
    st[start] = true;  // 在队列中的点为true，否则为false
    dis[start] = 0;
    
    while(q.size()){
        auto t = q.front();  
        q.pop();
        st[t] = false;
        // 遍历出队的临边
        for(int i = h[t]; ~i; i = ne[i]){
            int j = e[i];
            // 如果可以更新，并且队列中没有，那么就将这个点也加入队列当中
            if(dis[j] > dis[t] + w[i]){
                dis[j] = dis[t] + w[i];
                if(!st[j]){
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
}

int main(){
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while(m --){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    
    spfa(1);
    
    if(dis[n] == 0x3f3f3f3f) puts("impossible");
    else printf("%d", dis[n]);
    return 0;
}

spfa判断是否存在负环

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

const int N = 100010;
int h[N], e[N], ne[N], idx, w[N], dis[N], cnt[N];
bool st[N];
int n, m;
queue<int> q;

void add(int a, int b, int c){
    w[idx] = c, e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 当一个点被入队的次数大于能于n次则肯定存在负环，cnt数组表示到达当前这个点最短路的边数，
//如果cnt[x]>=n,说明至少经过了n条边，即n+1个点，由抽屉原理可知显然有两个点重复，即存在负环
bool spfa(){
    
    for(int i = 1; i <= n; ++ i){
        q.push(i);
        st[i] = i;
    }
    while(q.size()){
        auto t = q.front();
        q.pop();
        st[t] = false;
        for(int i = h[t]; ~i; i = ne[i]){
            int j = e[i];
            if(dis[j] > dis[t] + w[i]){
                dis[j] = dis[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if(cnt[j] >= n) return true;
                if(!st[j]){
                    q.push(j);
                    st[j] = true;
                }
            }
            
        }
    }
    return false;
}

int main(){
    scanf("%d%d", &n, &m); 
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; ++i){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    if(spfa()) puts("Yes");
    else puts("No");
    return 0;
}