支持向量机
本篇文章是我学习SVM的摘抄笔记,其中大量公式抄自JerryLead的同名博客。想拜读精彩的SVM博文,移步至此http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html
1、由线性判别模型引出
假设某一场景的数据集线性可分,那么如何确定一条最优或者次优的模型函数,我们可以通过引入最优间隔这个概念来确定一个性能最优的模型
2、函数间隔和几何间隔
给定一个训练样本![]() ,x是特征,y是结果标签。i表示第i个样本。我们定义函数间隔如下:
,x是特征,y是结果标签。i表示第i个样本。我们定义函数间隔如下:
当![]() =1时,其函数间隔
=1时,其函数间隔![]() 大于等于0,当=-1时,仍大于等于0。函数间隔表示出特征是正例还是反例的确信度。为了确定一个唯一的间隔距离,需要对函数间隔公式归一化,引入单位向量
大于等于0,当=-1时,仍大于等于0。函数间隔表示出特征是正例还是反例的确信度。为了确定一个唯一的间隔距离,需要对函数间隔公式归一化,引入单位向量![]() ,得到
,得到
我们需要通过设定||w|| = 1来固定参数序列![]() , 那么对于所有的训练样本,定义出全局最小几何间隔
, 那么对于所有的训练样本,定义出全局最小几何间隔
3、最优间隔分类器
寻找一个超平面,使得离超平面比较近的点能有更大的几何间隔。形式化的表示为
由于||w||=1不是凸函数,不好优化,通过几何间隔和函数间隔的关系![]() ,我们改写一下上面的式子:
,我们改写一下上面的式子:
此时的w不受||w||=1的约束,不能求得w和b的确定值,所以需要使![]() 固定全局函数间隔,那么几何间隔
固定全局函数间隔,那么几何间隔![]() ,并希望把目标函数变为可优化的凸函数,由于求
,并希望把目标函数变为可优化的凸函数,由于求![]() 的最大值相当于求
的最大值相当于求![]() 的最小值,所以上式可变性为
的最小值,所以上式可变性为
那么得出目标函数是二次函数,约束条件是线性函数的可进行二次规划的形式化问题
4、拉格朗日对偶
对有二次目标函数线性约束的问题,通常采用拉格朗日对偶问题的求解得到原始问题的最优解,那么我们先给出其拉格朗日表述形式
对于原始问题
通过以上变换我们将有约束的原始问题变为无约束的对偶问题,然后对对偶问题求解
为了套用公式,我们需将约束条件变为
带入拉格朗日公式为
注意到这里只有![]() 没有
没有![]() 是因为原问题中没有等式约束,只有不等式约束。
是因为原问题中没有等式约束,只有不等式约束。
5、求解
我们需要固定求参数w,b的极值,对w,b求偏导数,并使其偏导数等于0,则
能得到w关于的等式
我们将上式代入拉格朗日函数,能求得函数的最小值,代入化简为
我们得到只关于的拉格朗日算式,这样求的就能求得w和b,向量的长度等于样本的数量,其中![]() 可以表示为
可以表示为![]() 这种内积的形式,进一步求极大化
这种内积的形式,进一步求极大化
6、最大软间隔
实际上的数据场景并不如我们想象的那么理想,当比如图形有离群点(噪声),那么支持向量机就会考虑噪声点得到一个小间隔的线性模型,甚至可能找不一条线性可分的模型。我们通过最大软间隔模型来优化此场景下的模型。
最大软间隔的定义是允许一些点游离并在在模型中违背限制条件(函数间隔大于1),引入非负参数![]() (称为松弛变量),就允许某些样本点的函数间隔小于1。如果任意大的话,那所有的超平面都是符合条件的了。所以,在原来的目标函数后面加上一项,使得其总和也要最小:
(称为松弛变量),就允许某些样本点的函数间隔小于1。如果任意大的话,那所有的超平面都是符合条件的了。所以,在原来的目标函数后面加上一项,使得其总和也要最小:
原来的约束条件变为
其中C是一个预先定义好的常量,叫惩罚因子,代表对误差的宽容度,C越大,说明你越不能容忍出现误差,因为C越大意味着最小化的目标函数越大,使得最终间隔变小。
代入拉格朗日函数为
分别对w,b求导,最终得到
7、核函数
如果要解决的数据环境线性并不可分,需要使用核函数技巧
我们可以将原空间变换成一个更高维的空间,在这个高维的线性空间下,再用一个超平面进行划分。
映射到
假设模型是多项式分布的,我们可将
变换为
这样就把输入空间从二维向四维映射后,样本由线性不可分变成了线性可分,但是特征的维度变高了,计算难度加大,泛化能力降低(适应数据的能力)。
所以我们希望有一种函数方法可以近似的直接求得的方法来简化暴增的维数带来的复杂计算, 线性核函数如下
引入核函数概念的好处是,直接对核函数求值不会比线性空间增加过多额外的计算负担



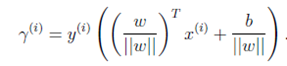

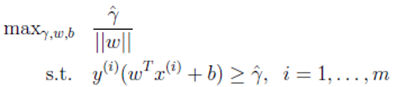
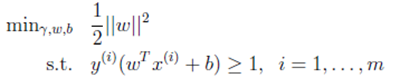
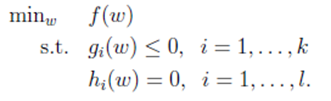
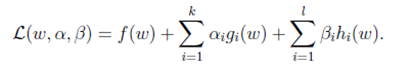
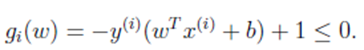
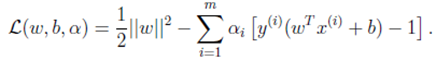
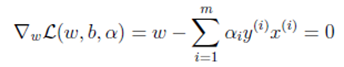
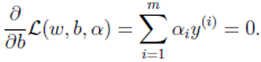
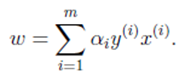
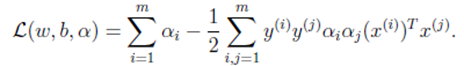
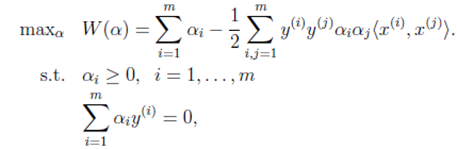
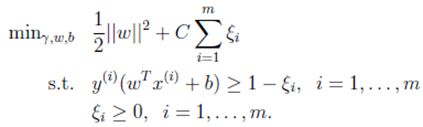
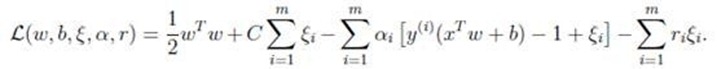
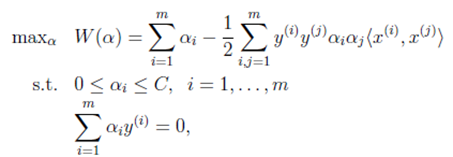
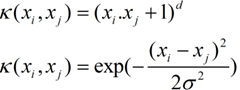

 浙公网安备 33010602011771号
浙公网安备 33010602011771号