一种利用穆斯堡尔效应收集宇宙空间中的带电等离子体的装置
一种利用穆斯堡尔效应收集宇宙空间中的带电等离子体的装置
在一个正方体中心,放置4个圆环状线圈,线圈中心放置一个圆环状电磁铁。在正方体的8个顶点上放置伽马射线发射装置,4个圆环状线圈通电后发射高频电磁波,圆环状电磁铁产生强磁场。这样的一个装置放置在宇宙空间中,就会吸收宇宙空间中的带电等离子体。由于8个顶点上的伽马射线向圆环电磁铁内部发射伽马射线,就会使内部的等离子体产生穆斯堡尔效应,就会吸收大量带电等离子体靠近。伽马射线使电磁铁内部的等离子体发生穆斯堡尔效应,吸引外面的呆呆牛等离子体进入带线圈内部
相关资料可见网址:https://www.123912.com/s/g0jijv-jYhl3?pwd=KQ6a# 提取码:KQ6a。
同时,圆环状电磁铁上面缠绕着超导线圈,它带电后就会形成强磁场。控制电流的强度就会控制磁场的强度。这个磁场的强度和电子绕原子核旋转时,电子的磁场强度相耦合,这样就会使磁场更好的控制带电等离子体的向内部运动。同时,用产生穆斯堡尔效应的谐振公式计算,8个顶点伽马射线发生器产生伽马射线的强度,就会更好的控制中心带电等离子体产生穆斯堡尔效应。其结构如下图所示:
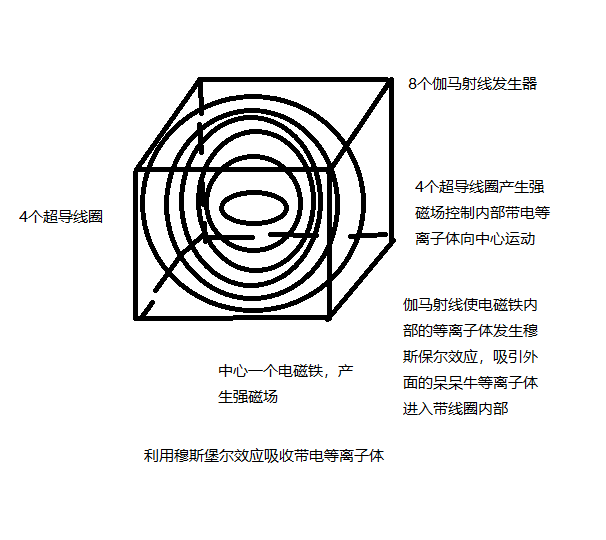
计算原子核内部电子的运动能量的方法如下所示:
下面的资料可见《理论物理》第二册《量子论与原子结构》,吴大猷著,科学出版社1983年出版。
电子自旋的角动量为
S(h/2π)
磁矩是
2s(eh/4πmc)=2sμ
s
反常zeeman效应的lande g公式
根据(1)式之假定及(7),(8),(10)等假设,我们即可解(1-19)式的lande g公式。在一2s+i Lj态的原子,其能量易变,可由下式(17)来表示,即(1-18)。
→ →
△E =gμ JHcos( J , H ) (1-17)
H s
此能量变易,乃系由于轨道运动及自旋运动所产生的磁矩,与外来磁场H间的交互作用而来,故可写为:
→ → → →
△E =μ H(Lcos( J , H )+2Scos( S ,H ) (1-18)
H s
第三章
依照电磁学中的Biot-Savart定律,距离一电流元素I为r的点0,
3
电流产生的磁场为[r*I]/cr (如图所示)
I=Zev
r
o
一个带正电荷Ze的原子核(距离电子为r),由于其(与电子相对的)运行而产生磁场。此磁场在电子所在处为
3 3
H=Ze[r*v]/cr =Ze[r*mv]/mcr
此处v代表原子核与电子的相对速度。因[r*mv]系电子与原子核的轨道运动的角动量
→
M =[-mv*r], (3-1)
在此磁场H中,自旋磁矩μ 的能量为
S
→ → 3
△E =(μ *H)=2μ*Zeh( l ,s )/mcr
s.o. s
2 → → 3 2 3 → →
=4μ Z( l * s )/r =4(eh/2mc) (Z/r )( l ,s ) (3-2)
s
→ →
如用余弦定理,可得( l , s )之值。
→ → 2 2 2
( l , s )=j -l -s )/2 [j(j+1)-l(l+1)-s(s+1)]/2 (3-3)
3
对于椭圆运动,r并非常数,故需将1/r 对一周期平均因此
2  ̄ 3
△E =2(eh/2mc) ( Z/r ) [j(j+1)-l(l+1)-s(s+1)] (3-4)
- O
上式当然并不十分正确,因电子与原子核的相对运动系一加速度运动,故从“实验室坐标”(laboratory coordinate system)转换到电子静止的坐标时。不能如上简单的推论。L.H.Thomas于1926年曾证明真正正确的结果,是在(2)及(4)式乘上一个因子“1/2”,即
2  ̄ 3 → → → →
△E =2(eh/2mc) ( Z/r )( l * s )≡2ζ( l * s )
- O
= ζ[j(j+1)-l(l+1)-s(s+1)] (3-5)
现在计算1/R 的平均值。此平均值可以bohr-sommerfeld理论(本册甲部,第五章第2节)计算之
 ̄ 3 3 3
1 /r =(1/2π)∮[(1+εcosφ)/(1-ε )] dφ
但正确的公式,则必须用量子力学计算,其结果是
 ̄ 3 3 3 3
1 /r =Z /[a n l(l+1/2)(l+1)
2 2
a =h /me (3-6)
0
由(5)及(6)式,对
L+s l+1/2
J={ ={
L-s l-1/2
两个能谐,由于自旋-轨道交互作用所产生的能量改变为
3 4 3 l/2 j=l+1/2
△E =Rα Z hc/[n l(l+1/2)(l+1){ 如 (3-7)
s.o -(l+1)/2 j=l-1/2
此处
2 4 3 2
R=2π me /ch ,α=e /hc=1/137。
h表示电磁波频率,c表示光速,m表示电子的质量,e表示电子的电量。
计算π可采用拉马努金公式:
∞ 4k
1/π=[2√2/(99*99)]∑[(4k)!(26390k+1103)]/(396 )
k=0
∞ 4m 4
1/π=[1/2√3]∑(8m+1)(4m)!/4√3) (m!)
m=0
(7)式中的两个值,乃相当于l 及 s 在平行及反平行的情况*。两能谐的能量差,称为“双重线间距”,为
3 4 3
△ν =Rα Z /n l(l+1) (3-8)
doubles
*观之,(7)式似示S态(l=0)之△E 变成无穷大。但按量子力学的准确计算,当l=0
s.o
时,自旋-轨道交互作用作,实等于零。
第四章
兹考虑单电子系统,并完全忽略自旋-轨道交互作用,在这种情况下:
△E =μ (l*H)+2μ (s*H)=(m +2m )μ H (5-4)
H s s i s s
此处m 及m 乃轨道及自旋量子数,满足下关系
-l≤m ≤l ; -1/2≤m ≤1/2, (5-5)
I s
令m代表全磁量子数
m=m +m (5-6)
I s
则(4)式可写为下列形式
△E =(m+m )BH (5-7)
H S
2 2
将上式应用于第一章第五节所述之 P → S 跃迁。
1/2,3/2 1/2
如l=1及s=1/2.m+m =m +2m 之可能值为
s l s
m+m =-2,-1,0,1,2
s
如l=0,s=1/2,则m+m =-1,0,1
S
如应用选择定则
△m=0,±1 (8-8)
2 2
则 S → P 之跃迁,将分解为三个分线,其分线之间距为μ H(见下图所示)。
1/2, 1/2,2/3 s
此情况与正常Zeeman效应完全一致。其次考虑在强磁场情形下的自旋-轨道交互作用,此时△E >>△E ,△E 见(3-2)式
H s.o
→ →
因l及s各自独立的绕着H旋转,故非向量乘积( l , s) ,之值,需作一长时间的平均值。从球面三角学知:
→ → → → → → → → → →
cos( l ,s )=cos( l , H )cos( s , H ) +sin( l , H )sin( s , H )cosφ
如对一长时间取平均,则cosφ之平均值为零。故得
→ → → → → →
(l * s )=lcos(l ,H )*scos( s ,H )=m m
l s
因此,在强磁场H情形下,
2 3
△E =2μ (Z/r )m m ≡ξm m (5-9)
s.o S l s l s
强磁场H所产生的总能量改变为
△E=△E +△E =(m+m )μ H+ξm m (5-10)
H s.o s s l s
P 及S 在弱场(反常Zeeman效应)及强场(Paschen-Back效应)中的能谐可由下
1/2,2/3 1/2,
图看出
在下图中得见,除了能谐的 ξ次的小移外(自旋-轨道作用,见(5-3)式) ,在强磁场中,反常Zeeman效应表现的寻常zeeman效应,非常相像。
当磁场在即不甚强亦不弱(即△E ≌△E )的情形下,
H s.o
zeeman效应变成非常复杂,在量子力学中这问题是有正确的叙述的。
- 在一弱磁场中,由于自旋-轨道交互作用及磁场所产生的能量,可由(3-7)式及(4-2)+(1-19)式来表示,即
△E =△E +△E =(m+m )μH+m m ξ ,△E >>△E
H s.o s l s H s.o
兹假设在任何磁场中, △E可用参数 ξ及 μH的二次式来表示。试证明二次式为
2 2 2 2
(△E ) +(ξ/2-2mμH)*△E+[-l(l+1)ξ /4-mξμH+(m -1/4)(μH) ]=0
第二部分 穆斯堡尔效应理论
下面的内容可见《穆斯堡尔效应及其应用》,夏元复,叶纯灏,张健编著,原子能出版社,1984年出版。
第四章
4.1穆斯堡尔源
为了观察到穆斯堡尔谱,首先必须有反冲γ辐射源即穆斯堡尔源,这通常是由会衰变到穆斯堡尔核的激发态母核产生的。常用于产生穆斯堡尔原子核激发态的核衰变过程是(参见图4.1):电子俘获(例如Co57的衰变),β衰变(例如Sm151的衰变),同质异能跃迁(例如Sn119m的同质异能跃迁)。此外,有时也可以由α衰变来获得某些穆斯堡尔同位素。例如利用半衰期为458年的Am241的α衰变可产生它的装置分离开来,单独使用几个半衰期。也有一些母核的半衰期短于一天,甚至只有几十分钟或更短得多,此时我们就常利用库伦激发,在加速器上将一束较高能量(大约10MeV)的带电粒子(例如O4+,CL7+)去轰击靶物质来产生穆斯堡尔γ跃迁。有时也可在反应堆旁利用(n,γ).(n,p)反应来产生穆斯堡尔跃迁的短寿命母核。但是,这两种方法都必须在加速器或反应堆旁,边产生母核,边做实验。
第三部分 电磁线圈的电磁场
电磁线圈内部通高压产生强磁场,控制等离子体向中心移动。电磁波的方程如下所示:
函数1:
f (x,y)=x*x*ln(√(x*x+y*y)),
1
ρ=sin(2θ)/12sin(2θ),
f (x,y)=x+y,
2
Round((√(x*x+y*y))
f (x,y)=│e │
3
f (x,y)=gcd(√(x*x+y*y),√(x*x+y*y))
4
Round(sec(√(x*x+y*y))
f (x,y)=-e
5
(√(x*x+y*y))
f (x,y)=sec[e ]
6
ρ=cos(4θ)/[12θ+5sin(2θ)],
f (x,y)=2cos(x+y)sin(x+y)/3,
7
(√(x*x+y*y))
f (x,y)=π
8
f (x,y)= gcd (√x,√y)sin(1/x)cos(1/y)/√2 ,
9
f (x,y)= 2sin[remain (√(2x-y),y)]/(x+y) ,
10
f (x,y)= sec[round(x+sin(y))/(√(x+y)*ln(x-y)
11
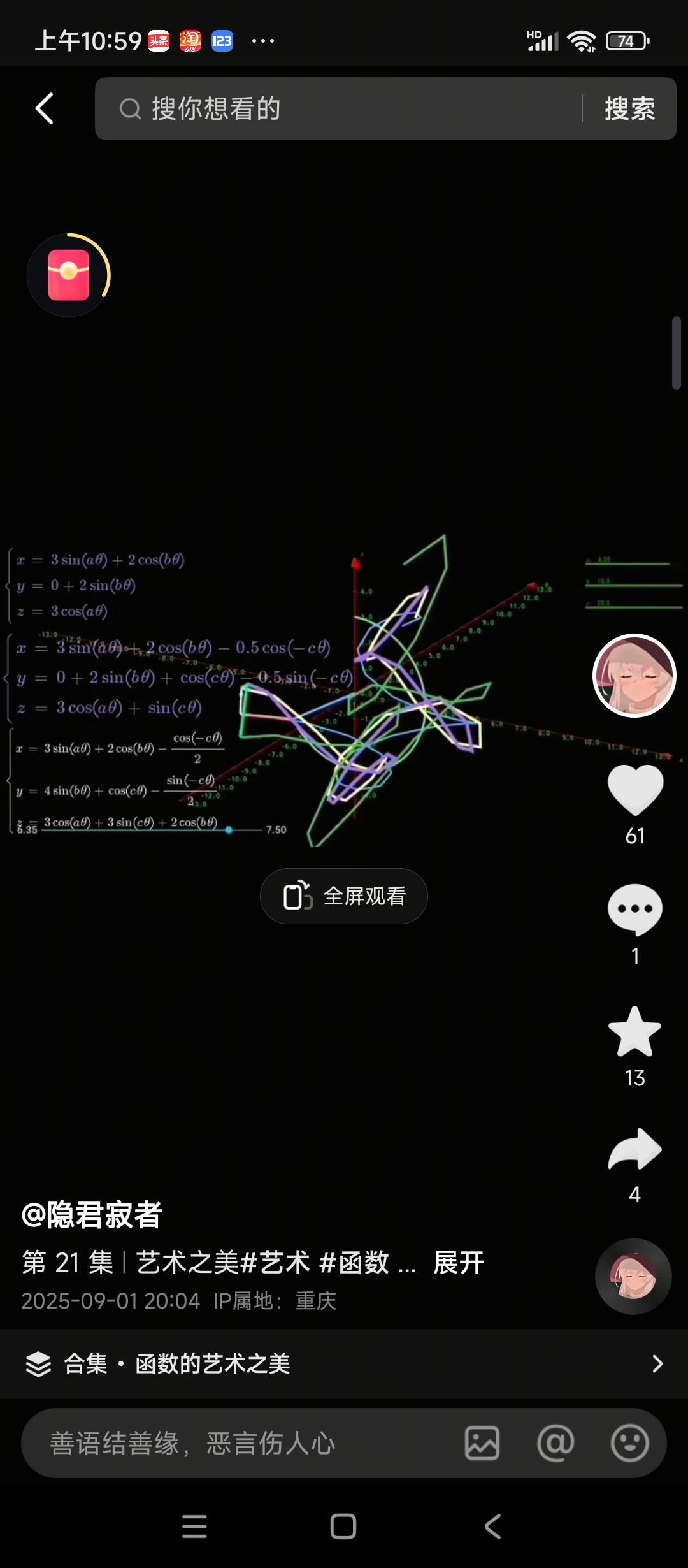
波形2:(卷轴函数,格相加中户函数,引力复窜函数)
f (x,y)= x*x+y*y ,
1
f (x,y)= f (x,y)sin(x),
2 1
Cos(θ) 5 5
ρ=sina(θ)(e +cos (5θ/12)-sin (5θ/12)),
t∈[0,2π],u∈[0,6π],
t
x=f (sin(e ), u/√t),
1
{
Y=tf (t,u),
1
Z=u,
Sinxcosy
x ≡(sin(3π/2),1-f (sin2,1))
│p(i-x)│ 1
f (x,y)=gcd(round(sinx+cosy-sinx)cosx )
3
f (x,y)= f (x,f (x,f (x,y)))/[f (x,y)+f (x,y)]
2 3 2 1 1 3
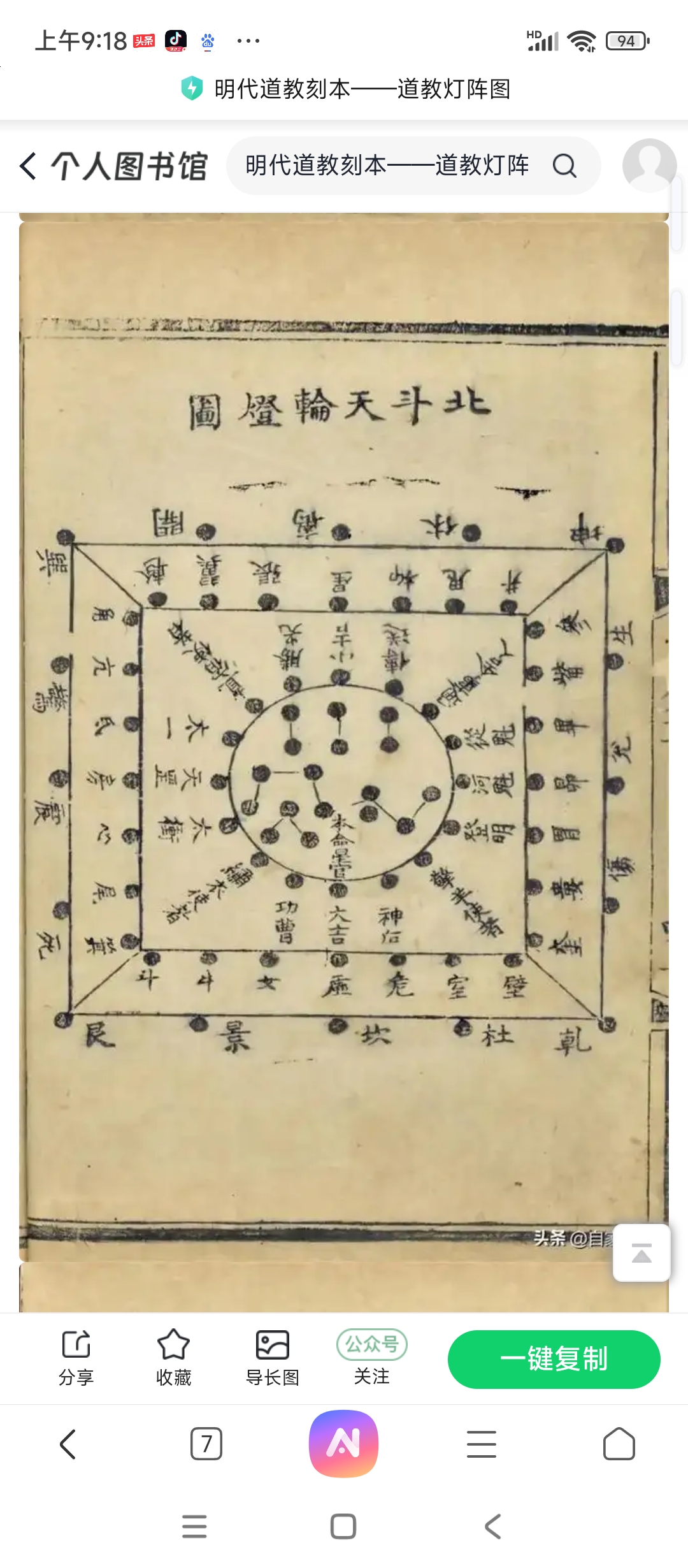
同时,在8个顶点发射伽马射线时,要求,发射源按照下面道教真灯图的形状发生移动,这样就会更好的产生穆斯堡尔效应。因为这个真等图的形状是以后有固定规律的图形,它是一个可以把平面坐标系区域分为具有整除性分布规律的图形。可见明代道教刻本(正统道藏)《道教灯阵图》,清代道教秘本《斗姥幡坛召亡灯符式》




















































 浙公网安备 33010602011771号
浙公网安备 33010602011771号