结对项目作业
简介
- 图形化版本(这是主要版本,包含了图形界面,以及集成的可下载直接运行APP,具体流程可在Github上查看)
- 作者:马泽琪 3118005016、张龙伟 3118005028
PSP:
| PSP | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | 估计这个任务需要多少时间 | 26*60 | 30*60 |
| Development | 开发 | ||
| Analysis | 需求分析 (包括学习新技术) | 4*60 | 6*60 |
| ·Design Spec | 生成设计文档 | 30 | 30 |
| ·Design Review | 设计复审 (和同事审核设计文档) | 60 | 2*60 |
| · Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 60 | 60 |
| ·Design | 具体设计 | 2*60 | 2*60 |
| ·Coding | 具体编码 | 10*60 | 12*60 |
| ·Code Review | 代码复审 | 2*60 | 3*60 |
| ·Test | 测试(自我测试,修改代码,提交修改) | 4*60 | 6*60 |
| Reporting | 报告 | ||
| ·Test Report | 测试报告 | 60 | 60 |
| ·Size Measurement | 计算工作量 | 30 | 30 |
| ·Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | ||
| 合计 | |||
效能分析
- 程序最消耗时间的应该是生成式子、计算式子、判断式子是否相同这三部分。
题目:
- 实现一个自动生成小学四则运算题目的命令行程序(也可以用图像界面,具有相似功能)。
说明:
- 自然数:0, 1, 2, …。
- 真分数:1/2, 1/3, 2/3, 1/4, 1’1/2, …。
- 运算符:+, −, ×, ÷。
- 括号:(, )。
- 等号:=。
- 分隔符:空格(用于四则运算符和等号前后)。
- 算术表达式:
需求:
- 控制生成题目的个数
- 控制题目中数值(自然数、真分数和真分数分母)的范围
- 生成的题目中计算过程不能产生负数,也就是说算术表达式中如果存在形如e1− e2的子表达式,那么e1≥ e2。
- 生成的题目中如果存在形如e1÷ e2的子表达式,那么其结果应是真分数。
- 每道题目中出现的运算符个数不超过3个。
- 程序一次运行生成的题目不能重复,即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。例如,23 + 45 = 和45 + 23 = 是重复的题目,6 × 8 = 和8 × 6 = 也是重复的题目。3+(2+1)和1+2+3这两个题目是重复的,由于+是左结合的,1+2+3等价于(1+2)+3,也就是3+(1+2),也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题,因为1+2+3等价于(1+2)+3,而3+2+1等价于(3+2)+1,它们之间不能通过有限次交换变成同一个题目。
生成的题目存入执行程序的当前目录下的Exercises.txt文件,格式如下:
- 四则运算题目1
- 四则运算题目2
……
其中真分数在输入输出时采用如下格式,真分数五分之三表示为3/5,真分数二又八分之三表示为2’3/8。
7.在生成题目的同时,计算出所有题目的答案,并存入执行程序的当前目录下的Answers.txt文件,格式如下:
- 答案1
- 答案2
特别的,真分数的运算如下例所示:1/6 + 1/8 = 7/24。
- 程序应能支持一万道题目的生成。
- 程序支持对给定的题目文件和答案文件,判定答案中的对错并进行数量统计,输入参数如下:
Myapp.exe -e <exercisefile>.txt -a <answerfile>.txt
统计结果输出到文件Grade.txt,格式如下:
Correct: 5 (1, 3, 5, 7, 9)
Wrong: 5 (2, 4, 6, 8, 10)
其中“:”后面的数字5表示对/错的题目的数量,括号内的是对/错题目的编号。为简单起见,假设输入的题目都是按照顺序编号的符合规范的题目。
遇到的困难及解决方法
困难描述
- 张龙伟同学负责中缀表达式转后缀表达式的部分。这个是数据结构课程中在栈中学习到的,由于经常划水所以不是很熟练,但做起来也不是很难。但是这个中缀转后缀,还是着实废了不少时间
- 马泽琪负责主要代码的编写和封装,包括题目生成、判别、界面,编写过程最主要的想法是封装可复用代码,当然这个要确定好规范,在编写的过程中明确输入输出。图形化界面也是从0入手,QT适合PC端编程,于是就放弃了较为古老的MFC
做过哪些尝试
- 在编写的过程中。最主要的目标还是代码的可复用,还有程序的效率,也是尝试用了一些方法,但是效果都很一般,毕竟在一次性生成10000道题目是需要很大的算力的,现在有一个想法,就是把一次性生成转化为多次生成,这还需要在以后尝试。
关键代码or设计说明
程序组成
生成式子以及计算的组成头
#pragma once #ifndef __QUESTION_HEAD__ #define __QUESTION_HEAD__ #include<string> #include"../PCal_Head/Fraction.h" using namespace std; //此类用于生成随机问题 class Question_Gen{ private: //需要生成的问题的数量 int Questions_Sum; //参与计算的最大值 int Cal_Max_Num; //参与计算的最小值 int Cal_Min_Num; //动态变化的值,统计已生成的问题数量 int Questions_Total; //中间结果的个数 int *Inter_Result_Total; //问题栈 string *Questions_Str; //后缀表达式,数和运算符间有空格 string *Postfix_Ex; //结果,用分数表示 Fraction *Results; //保存中间结果,即为每个问题后缀表达式计算过程中出栈的数 Fraction **Inter_Result; public: //友元 friend class Question_Cal; //构造函数 Question_Gen(); //参与计算的最大值 Question_Gen(int In_Max_Num); //生成一个问题 string Question_Gen_One(); //生成多个问题,并保存 bool Question_Gen_Many_Save(int Nums); //随机生成一个在left到right的数 int Random(int Left, int Right); //返回+-*/符号 string Cal_Char_Gen(int Char_Site); //辨别式子是否重复出现 bool Ex_IsSame(string Ques); //判断式子的结果,或者中间计算过程的数字是否超过Cal_Max_Num bool Ex_IsNo(); //返回第index个问题的答案 string Get_Index_Ans(int index); //返回第index个问题 string Get_Index_Ex(int index); //返回第index个问题的后缀表达式 string Get_Index_Post_Ex(int index); int Get_Questions_Total(); //将数量设成0 void Set_Ques_Total_Zeros(); void Set_Cal_Max_Num(int Nums); //设置题目数量 void Set_Ques_Num(int Num); int Get_Ques_Num(); }; //此类用于计算问题 class Question_Cal{ public: Question_Cal(); //友元 //friend class Question_Gen; //中缀转后缀 string Postfix_Ex_Gen(string Ques); //将后缀表达式进行计算,返回值的个数, Value_S是一个一维数组,返回中间值的个数,并且将中间值写入到一维数组中去,Ques是后缀表达式 int Postfix_Ex_Cal(Fraction *Value_S, string Ques); //两个数之间的计算 Fraction Fra_Cal(Fraction a, Fraction b, char x); }; #endif
生成问题
string Question_Gen::Question_Gen_One(){ string Question_i = ""; //运算符的数量 int Opera_Char_Sum = Random(1, 3); //运算数的数量 //int Opera_Num_Sum = Opera_Char_Sum + 1; string Opera_Char; string Opera_Num; int Opera_Num_i; int Opera_Char_i; //先生成一个单运算符的式子,如果1则生成一个分数 if (Random(0, 1) == 1){ int Numerator = Random(Cal_Min_Num, Cal_Max_Num); int Denominator = Random(Cal_Min_Num, Cal_Max_Num); Fraction Fra(Numerator, Denominator); Question_i += Fra.ToString() + ' '; } else { Opera_Num_i = Random(Cal_Min_Num, Cal_Max_Num); Opera_Num = to_string(Opera_Num_i); Question_i += Opera_Num + ' '; } Opera_Char_i = Random(0, 3); Opera_Char = Cal_Char_Gen(Opera_Char_i); Question_i += Opera_Char + ' '; if (Random(0, 1) == 1){ int Numerator = Random(Cal_Min_Num, Cal_Max_Num); int Denominator = Random(Cal_Min_Num, Cal_Max_Num); Fraction Fra(Numerator, Denominator); Question_i += Fra.ToString() + ' '; } else { Opera_Num_i = Random(Cal_Min_Num, Cal_Max_Num); Opera_Num = to_string(Opera_Num_i); Question_i += Opera_Num + ' '; } //运算符不只一个 for (int i = 1; i < Opera_Char_Sum; i++){ int R_Brackets = Random(0, 1); //是否加上括号 if (R_Brackets){ Question_i = "(" + Question_i + ") "; } Opera_Char_i = Random(0, 3); Opera_Char = Cal_Char_Gen(Opera_Char_i); Question_i += Opera_Char + ' '; //1则为分数 if (Random(0, 1) == 1){ int Numerator = Random(Cal_Min_Num, Cal_Max_Num); int Denominator = Random(Cal_Min_Num, Cal_Max_Num); Fraction Fra(Numerator, Denominator); Question_i += Fra.ToString() + ' '; } else { Opera_Num_i = Random(Cal_Min_Num, Cal_Max_Num); Opera_Num = to_string(Opera_Num_i); Question_i += Opera_Num + ' '; } } if (Ex_IsSame(Question_i) || Ex_IsNo()){ return ""; } Questions_Str[Questions_Total++] = Question_i; return Question_i; }
判断式子是否重复
bool Question_Gen::Ex_IsSame(string Ques){ Question_Cal Cal; //得到后缀表达式 Postfix_Ex[Questions_Total] = Cal.Postfix_Ex_Gen(Ques); string Post_Q_Str = Postfix_Ex[Questions_Total]; //得到中间结果的个数 int Value_Sum = Cal.Postfix_Ex_Cal(Inter_Result[Questions_Total], Post_Q_Str); //将最终结果存入Result Results[Questions_Total] = Inter_Result[Questions_Total][Value_Sum - 1]; Inter_Result_Total[Questions_Total] = Value_Sum; bool IsSame = false; for (int i = 0; i < Questions_Total; i++){ if (Inter_Result_Total[i] != Inter_Result_Total[Questions_Total]){ continue; } bool Is_Fist = true; for (int j = Inter_Result_Total[i] - 1; j >= 0; j--) { //如果是最后栈顶的一个数 if (Is_Fist) { Is_Fist = false; if (Inter_Result[i][j].Subtract(Inter_Result[Questions_Total][j]).GetNumerator() != 0) { break; } //如果是出栈的一对数 } else { //有不相等的就不用往下了 if (!((Inter_Result[i][j].Subtract(Inter_Result[Questions_Total][j]).GetNumerator() == 0 && Inter_Result[i][j - 1].Subtract(Inter_Result[Questions_Total][j - 1]).GetNumerator() == 0) || (Inter_Result[i][j - 1].Subtract(Inter_Result[Questions_Total][j]).GetNumerator() == 0 && Inter_Result[i][j - 1].Subtract(Inter_Result[Questions_Total][j]).GetNumerator() == 0))) { break; } //因为考虑了两个成对的数,所以再-1 j--; //如果一条式子可以找到最后,那么说明他们相等 if (j == 0){ IsSame = true; return IsSame; } } } } if (Questions_Total == 0){ IsSame = false; } return IsSame; }
中缀转后缀
/中缀转后缀 string Question_Cal::Postfix_Ex_Gen(string Ques){ string PostQ = ""; stack <char> Char_S; int i = 0; while (i <= Ques.length() - 1){ //值为数字时 if (Ques[i] >= '0' && Ques[i] <= '9'){ while (Ques[i] >= '0' && Ques[i] <= '9'){ PostQ += Ques[i]; i++; } //遇到空格要加上空格 if (Ques[i] == ' ' || Ques[i] == '\0' || Ques[i] == ')') { PostQ += ' '; if (Ques[i] == '\0') break; } if(Ques[i] == '\''){ PostQ += '\''; i++; } if (Ques[i] == '/'){ PostQ += '/'; i++; } continue; } //遇到左括号想都不用想直接push else if (Ques[i] == '('){ Char_S.push(Ques[i]); } else if (Ques[i] == ')'){ while (Char_S.top() != '('){ PostQ += Char_S.top(); Char_S.pop(); } PostQ += ' '; Char_S.pop();//把(输出。 } else if (Ques[i] == '-' || Ques[i] == '+'){ if (Char_S.empty() == 1 || Char_S.top() == '('){ Char_S.push(Ques[i]); } else{ while (Char_S.empty() != 1){ if (Char_S.top() == '('){ break; } PostQ += Char_S.top(); Char_S.pop(); } Char_S.push(Ques[i]); PostQ += ' '; } } else if (Ques[i] == '*' || Ques[i] == '/'){ if (Char_S.empty() == 1 || Char_S.top() == '(' || Char_S.top() == '+' || Char_S.top() == '-'){ Char_S.push(Ques[i]); } else{ while (Char_S.empty() != 1){ if (Char_S.top() == '('){ break; } PostQ += Char_S.top(); Char_S.pop(); } Char_S.push(Ques[i]); PostQ += ' '; } } i++; } while (Char_S.empty() != 1){ PostQ += Char_S.top(); Char_S.pop(); } //PostQ += ' '; return PostQ; }
计算后缀表达式
int Question_Cal::Postfix_Ex_Cal(Fraction *Value_S, string Ques){ int Total = 0; //计算值的个数 stack <Fraction> Postfix_S; int i = 0; bool IsRNumertor = false;//当出现1'1/2之类的数 int RNumer = 0; while (Ques[i] != '\0'){ if (Ques[i] == ' '){ i++; continue; } //cout << Ques.length() <<endl; // 遇到数则push到栈中 if (Ques[i] >= '0' && Ques[i] <= '9'){ Fraction fra; int Numerator; int Denominator; Numerator = atoi(&Ques[i]); while (Ques[i] >= '0' && Ques[i] <= '9') i++; if (Ques[i] == '\''){ i += 1; IsRNumertor = true; RNumer = Numerator; continue; } if (Ques[i] == '/'){ i += 1; Denominator = atoi(&Ques[i]); while (Ques[i] >= '0' && Ques[i] <= '9') i++; if (IsRNumertor == true){ Numerator += RNumer * Denominator; IsRNumertor = false; } Fraction f(Numerator, Denominator); fra = f; } else { Fraction f(Numerator, 1); fra = f; } Postfix_S.push(fra); } else { //遇到符号则弹出两个数出来运算 Fraction Num1, Num2; Num2 = Postfix_S.top(); Postfix_S.pop(); Value_S[Total++] = Num2; Num1 = Postfix_S.top(); Postfix_S.pop(); Value_S[Total++] = Num1; Fraction Result = Fra_Cal(Num1, Num2, Ques[i]); Postfix_S.push(Result); i++; } } Fraction value = Postfix_S.top(); Postfix_S.pop(); Value_S[Total++] = value; return Total; }
UI界面
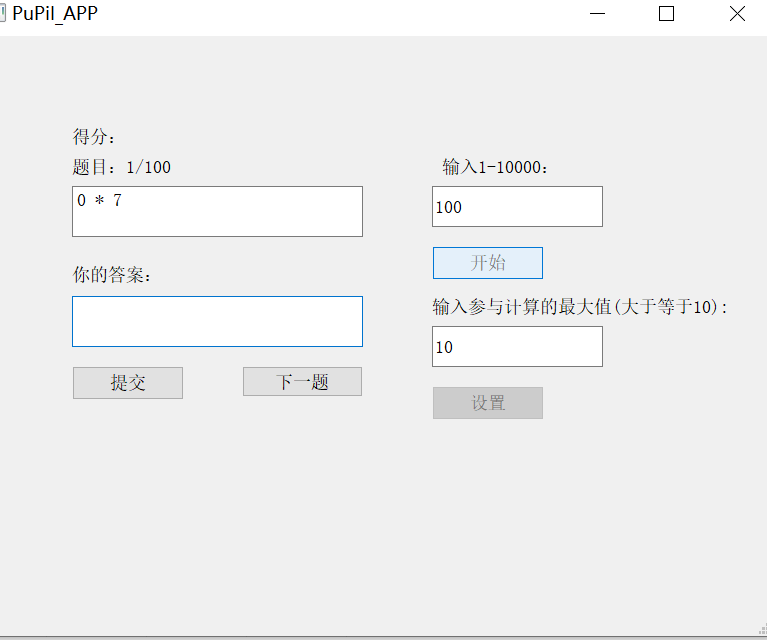
说明:
- 首先,要设置题目的数量,可以输入1-10000道题(10000道题可能需要点时间)
- 接着,要设置参与计算的最大值
- 这两个设置好才能继续运行
运行
- 输入数字后点击提交,提交的答案会进行比对,同时会显示答对的题数即得分
- 支持10000道题的生成
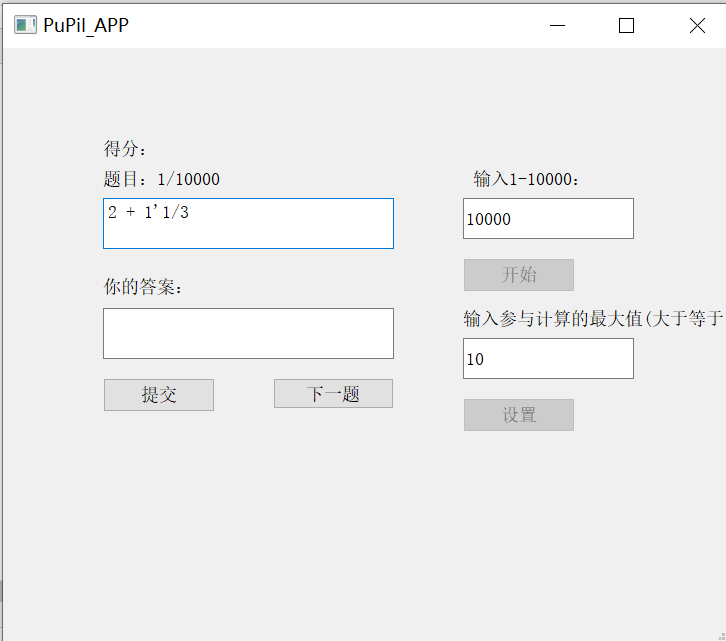
生成的题目
- 左边为题目,右边为答案(在PCal_Files中)
- 一万道题(且不重复)

历史记录
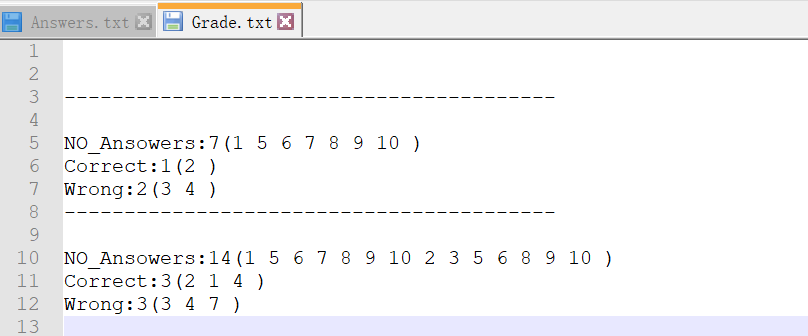
- Grade.txt(在PCal_Files中)
- 记录没回答的题目、回答正确的题目、回答错误的题目
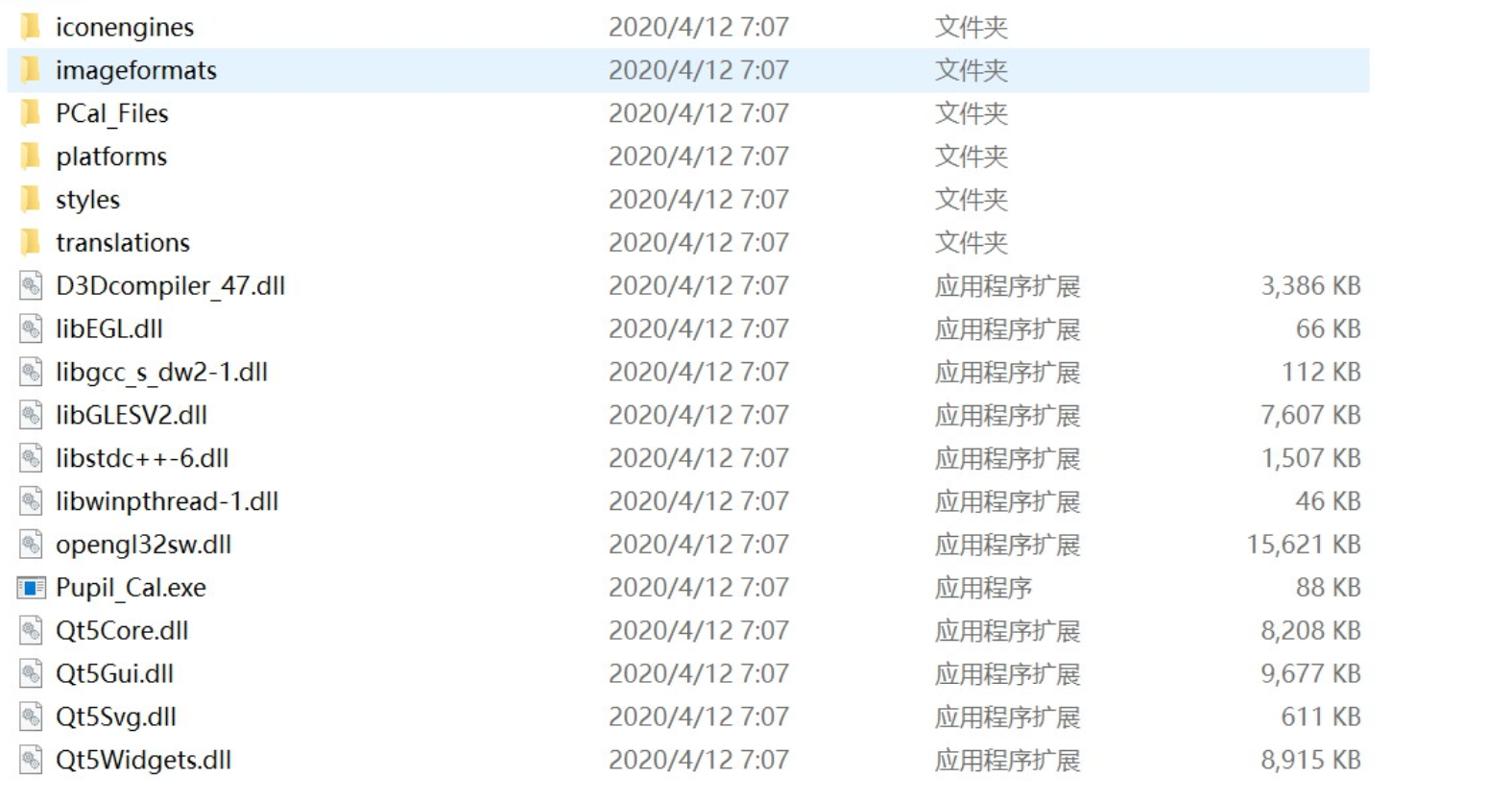
Pupil_APP可直接运行软件文件夹,程序运行输出的txt 存放在PCal_Files中




 浙公网安备 33010602011771号
浙公网安备 33010602011771号