matlab实验4-共轭梯度法程序设计

function conjugate_gradient_experiment()
    % 求解无约束优化问题:
    % f(x) = (x1 + 10x2)^2 + 5(x3 - x4)^2 + (x2 - 2x3)^4 + 10(x1 - x4)^4
    
    % 清除工作空间和关闭所有图形
    clc;
    clear;
    close all;
    
    % 定义目标函数和梯度
    syms x1 x2 x3 x4;
    f = (x1 + 10*x2)^2 + 5*(x3 - x4)^2 + (x2 - 2*x3)^4 + 10*(x1 - x4)^4;
    grad_f = gradient(f, [x1, x2, x3, x4]);
    
    % 转换为MATLAB函数
    f_func = matlabFunction(f, 'Vars', {[x1; x2; x3; x4]});
    grad_func = matlabFunction(grad_f, 'Vars', {[x1; x2; x3; x4]});
    
    % 定义不同的初始点（与实验二、实验三相同的初始点）
    initial_points = {
        [1; 1; 1; 1],    % 初始点1
        [2; 0; -1; 3],    % 初始点2
        [-1; 2; 0; -2],   % 初始点3
        [0; 0; 0; 0]      % 初始点4
    };
    
    % 参数设置
    max_iter = 10000;      % 最大迭代次数
    tolerance = 1e-6;      % 收敛容差
    
    % 存储结果
    results = cell(length(initial_points), 1);
    
    % 对每个初始点运行FR共轭梯度法
    for i = 1:length(initial_points)
        x0 = initial_points{i};
        fprintf('\n===== 初始点: [%g, %g, %g, %g] =====\n', x0(1), x0(2), x0(3), x0(4));
        
        [x_opt, f_opt, iter, x_history, f_history] = ...
            FR_conjugate_gradient(f_func, grad_func, x0, max_iter, tolerance);
        
        % 存储结果
        results{i}.initial_point = x0;
        results{i}.x_opt = x_opt;
        results{i}.f_opt = f_opt;
        results{i}.iterations = iter;
        results{i}.x_history = x_history;
        results{i}.f_history = f_history;
        
        % 显示结果
        fprintf('最优解: [%g, %g, %g, %g]\n', x_opt(1), x_opt(2), x_opt(3), x_opt(4));
        fprintf('最优值: %g\n', f_opt);
        fprintf('迭代次数: %d\n', iter);
    end
    
    % 绘制收敛曲线
    plot_convergence(results);
    
    % 保存结果到文件
    save_results(results);
end

function [x_opt, f_opt, iter, x_history, f_history] = ...
    FR_conjugate_gradient(f_func, grad_func, x0, max_iter, tolerance)
    % FR (Fletcher-Reeves) 共轭梯度法实现
    
    x = x0;
    g = grad_func(x);
    d = -g;  % 初始搜索方向为负梯度方向
    iter = 0;
    
    % 存储历史记录
    x_history = zeros(length(x0), max_iter+1);
    f_history = zeros(1, max_iter+1);
    
    x_history(:, 1) = x;
    f_history(1) = f_func(x);
    
    while norm(g) > tolerance && iter < max_iter
        % 线搜索 - 使用Wolfe条件或简单回溯法
        alpha = backtracking_line_search(f_func, grad_func, x, d);
        
        % 更新点
        x_new = x + alpha * d;
        g_new = grad_func(x_new);
        
        % Fletcher-Reeves beta
        beta = (g_new' * g_new) / (g' * g);
        
        % 更新搜索方向
        d_new = -g_new + beta * d;
        
        % 更新变量
        x = x_new;
        g = g_new;
        d = d_new;
        iter = iter + 1;
        
        % 存储历史记录
        x_history(:, iter+1) = x;
        f_history(iter+1) = f_func(x);
    end
    
    % 裁剪未使用的预分配空间
    x_history = x_history(:, 1:iter+1);
    f_history = f_history(1:iter+1);
    
    % 返回结果
    x_opt = x;
    f_opt = f_func(x);
end

function alpha = backtracking_line_search(f_func, grad_func, x, d)
    % 回溯线搜索
    
    alpha = 1;          % 初始步长
    rho = 0.5;          % 收缩因子
    c = 1e-4;           % 充分下降常数
    
    f = f_func(x);
    g = grad_func(x);
    slope = g' * d;     % 方向导数
    
    while f_func(x + alpha * d) > f + c * alpha * slope
        alpha = rho * alpha;
        
        % 防止步长过小
        if alpha < 1e-10
            break;
        end
    end
end

function plot_convergence(results)
    % 绘制收敛曲线
    
    figure;
    colors = lines(length(results));
    
    for i = 1:length(results)
        f_history = results{i}.f_history;
        iterations = 0:length(f_history)-1;
        
        semilogy(iterations, f_history, 'Color', colors(i,:), 'LineWidth', 1.5, ...
            'DisplayName', sprintf('初始点 [%g,%g,%g,%g]', results{i}.initial_point));
        hold on;
    end
    
    xlabel('迭代次数');
    ylabel('目标函数值 (log scale)');
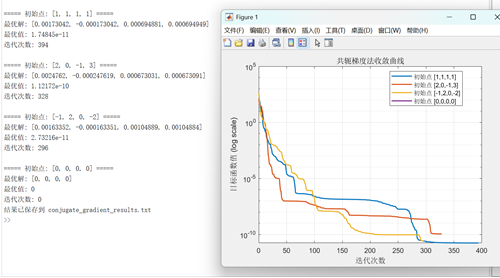
    title('共轭梯度法收敛曲线');
    legend('Location', 'best');
    grid on;
    hold off;
    
    % 保存图形
    saveas(gcf, 'conjugate_gradient_convergence.png');
end

function save_results(results)
    % 将结果保存到文本文件
    
    fid = fopen('conjugate_gradient_results.txt', 'w');
    
    fprintf(fid, '共轭梯度法实验结果\n\n');
    fprintf(fid, '%-20s %-30s %-15s %-10s\n', '初始点', '最优解', '最优值', '迭代次数');
    fprintf(fid, '--------------------------------------------------------------------\n');
    
    for i = 1:length(results)
        res = results{i};
        fprintf(fid, '[%5.2f,%5.2f,%5.2f,%5.2f]  ', res.initial_point);
        fprintf(fid, '[%8.6f,%8.6f,%8.6f,%8.6f]  ', res.x_opt);
        fprintf(fid, '%12.6e  %5d\n', res.f_opt, res.iterations);
    end
    
    fclose(fid);
    disp('结果已保存到 conjugate_gradient_results.txt');
end