matlab实验3-Newton法程序设计

function newton_method_optimization()
    % 初始点设置（可自行修改测试多个起点）
    x = [1; 1; 1; 1];
    
    % 停止条件与最大迭代次数
    tolerance = 1e-6;
    maxIterations = 100;
    iteration = 0;

    % 打印表头
    fprintf('Iter\t||Gradient||\tFunction Value\n');

    while iteration < maxIterations
        grad = computeGradient(x);
        hess = computeHessian(x);

        gradNorm = norm(grad);
        fprintf('%d\t%e\t%e\n', iteration, gradNorm, objectiveFunction(x));

        % 检查停止条件
        if gradNorm < tolerance
            break;
        end

        % 计算更新方向并更新变量
        direction = -hess \ grad;
        x = x + direction;
        iteration = iteration + 1;
    end

    % 输出最终结果
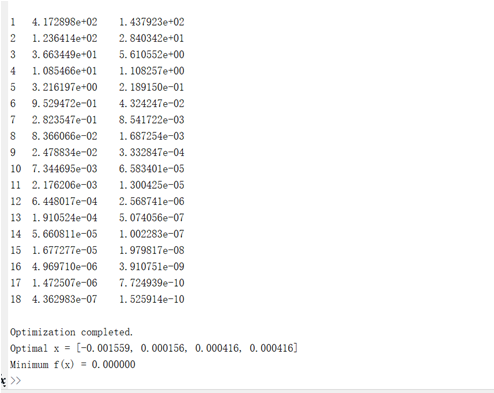
    fprintf('\nOptimization completed.\n');
    fprintf('Optimal x = [%.6f, %.6f, %.6f, %.6f]\n', x);
    fprintf('Minimum f(x) = %.6f\n', objectiveFunction(x));
end

% ------------------ 目标函数 ------------------
function value = objectiveFunction(x)
    value = (x(1) + 10*x(2))^2 + ...
            5*(x(3) - x(4))^2 + ...
            (x(2) - 2*x(3))^4 + ...
            10*(x(1) - x(4))^4;
end

% ------------------ 梯度函数 ------------------
function grad = computeGradient(x)
    grad = zeros(4,1);
    grad(1) = 2*(x(1) + 10*x(2)) + 40*(x(1) - x(4))^3;
    grad(2) = 20*(x(1) + 10*x(2)) + 4*(x(2) - 2*x(3))^3;
    grad(3) = 10*(x(3) - x(4)) - 8*(x(2) - 2*x(3))^3;
    grad(4) = -10*(x(3) - x(4)) - 40*(x(1) - x(4))^3;
end

% ------------------ Hessian矩阵函数 ------------------
function H = computeHessian(x)
    H = zeros(4,4);

    % 二阶导数计算（Hessian矩阵）
    H(1,1) = 2 + 120*(x(1) - x(4))^2;
    H(1,2) = 20;
    H(1,3) = 0;
    H(1,4) = -120*(x(1) - x(4))^2;

    H(2,1) = 20;
    H(2,2) = 200 + 12*(x(2) - 2*x(3))^2;
    H(2,3) = -24*(x(2) - 2*x(3))^2;
    H(2,4) = 0;

    H(3,1) = 0;
    H(3,2) = -24*(x(2) - 2*x(3))^2;
    H(3,3) = 10 + 48*(x(2) - 2*x(3))^2;
    H(3,4) = -10;

    H(4,1) = -120*(x(1) - x(4))^2;
    H(4,2) = 0;
    H(4,3) = -10;
    H(4,4) = 10 + 120*(x(1) - x(4))^2;
end