python实现排序算法
目录
python实现排序算法
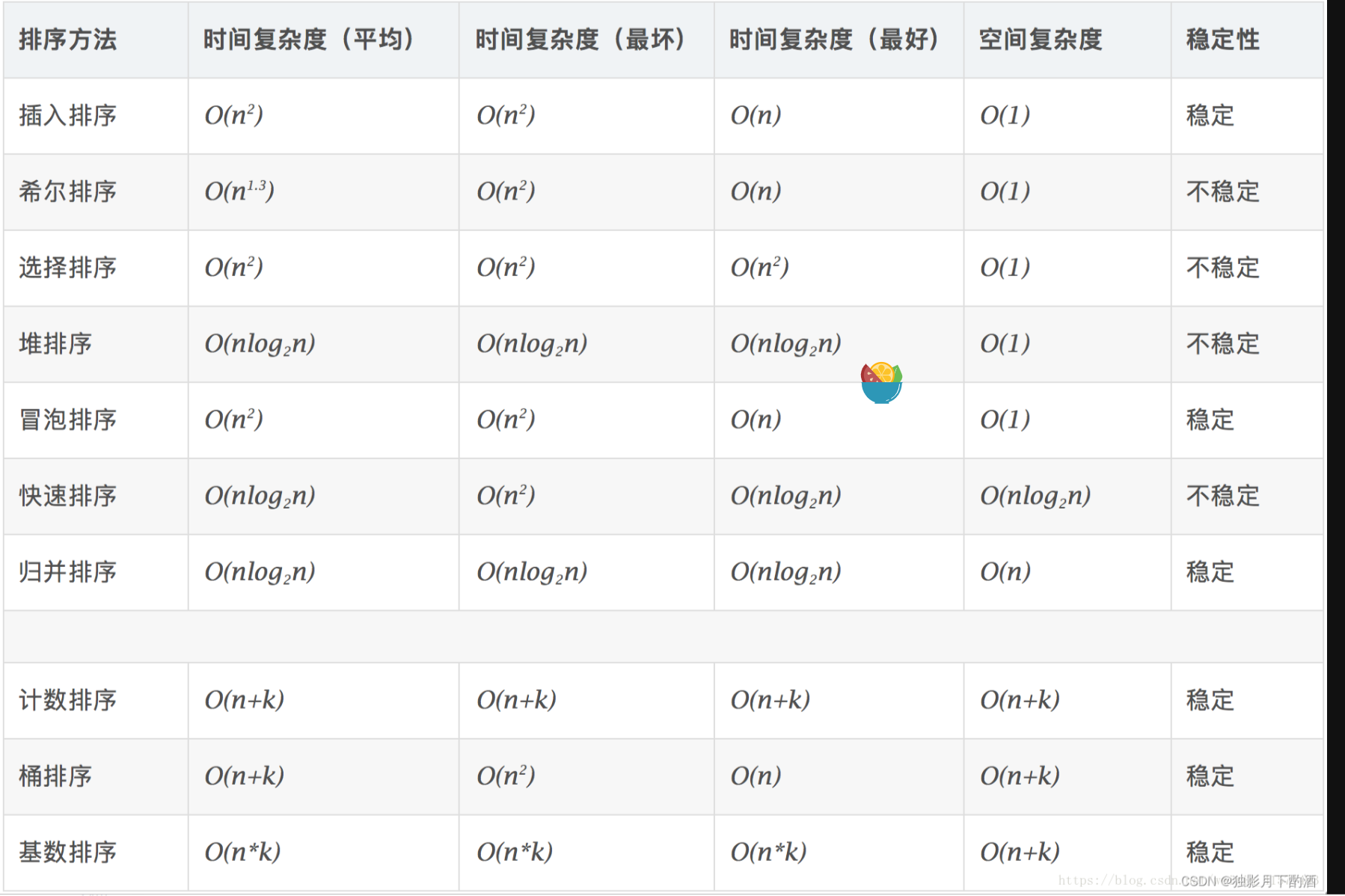
算法的时间复杂度\空间复杂度\稳定性
冒泡排序(Bubble Sort)
冒泡排序是一种简单的排序算法.它重复地遍历待排序的序列,依次比较两个元素,如果它们的顺序错误就把它们交换过来.算法的名字由来就是因为越小的元素会经由交换慢慢"浮"到数列的顶端.
算法特点
什么时候最快(Best Cases): 当输入的数据已经是正序
什么时候最慢(Best Cases): 当输入的数据已经是反序
算法图解
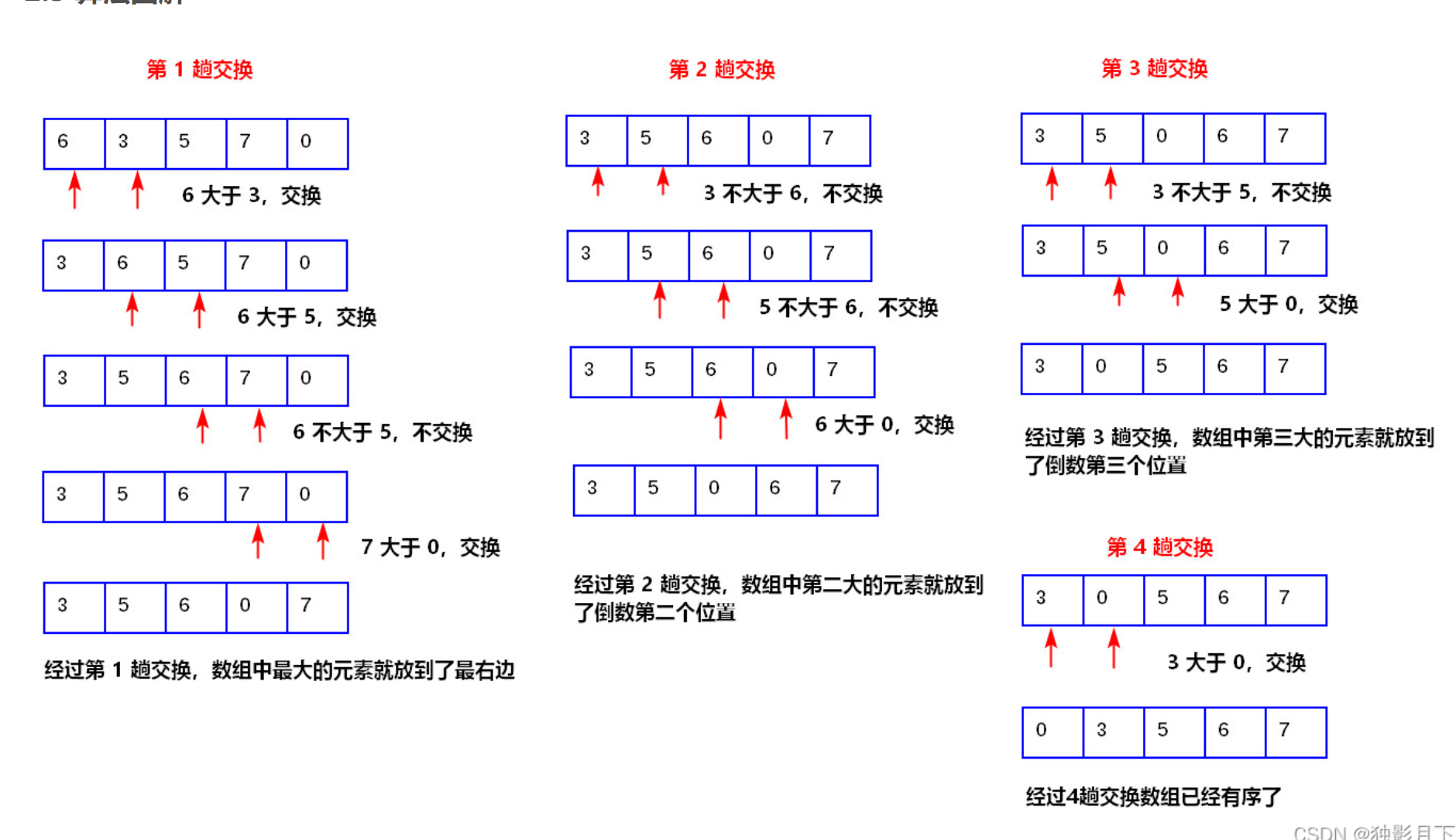
- 比较相邻的元素,如果第一个比第二个元素大,就交换,小于就不交换
- 对于每一对相邻的两个元素进行相同的操作,直到最后一组,保证最后一个是最大值
- 重复第一步和第二步,直到排序完成
代码展示
arr = [1, 23, 4, 56, 7, 87, 0]
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]: # 第一个数字>第二个数字
arr[j], arr[j + 1] = arr[j + 1], arr[j] # 位置交换
print(n) # 7
print(arr) # [0, 1, 4, 7, 23, 56, 87]
选择排序(Selection Sort)
选择排序的数据都是O(n*2)的时间复杂度.
算法特点
数据规模越小越好
不占额外的内存空间
算法图解
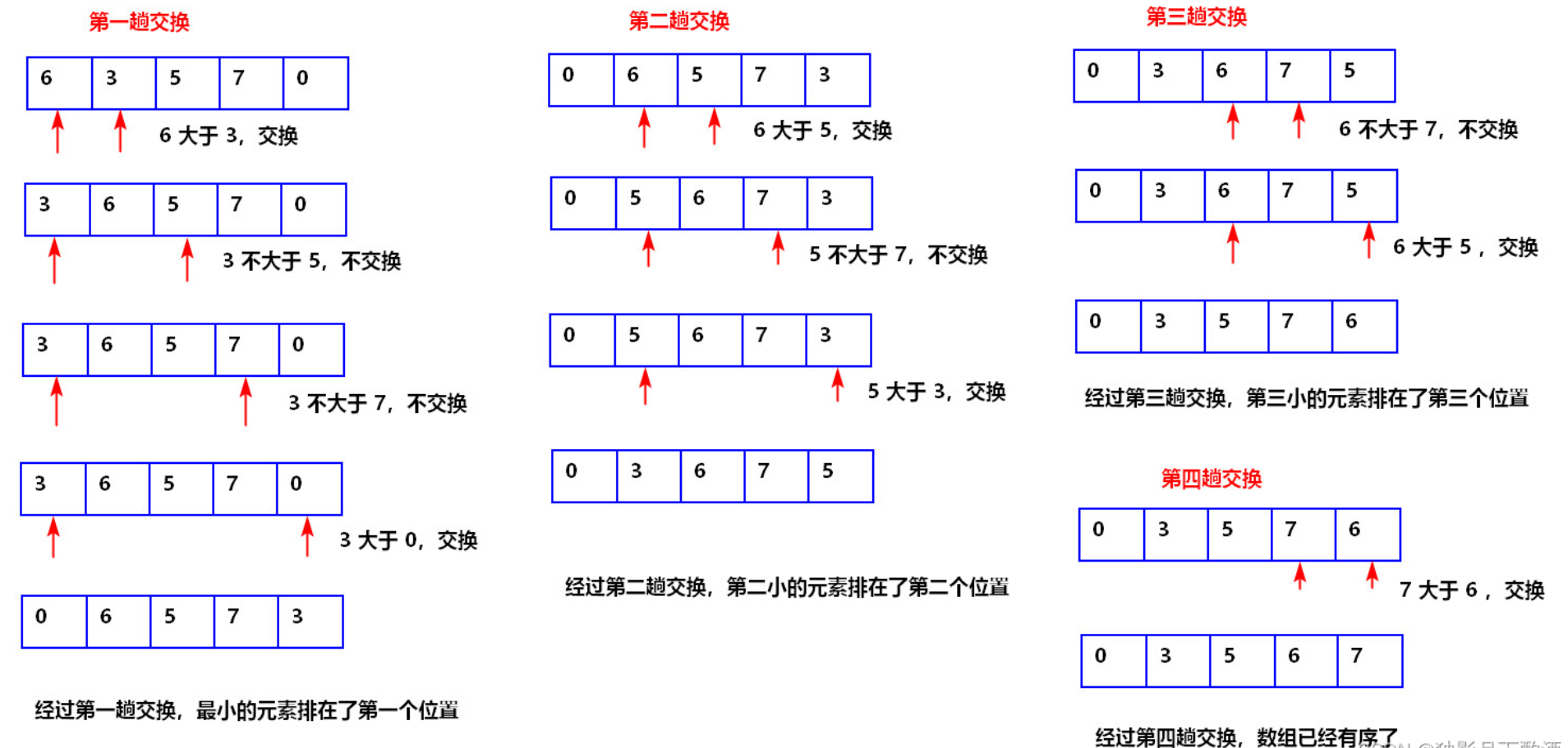
- 首先在末排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 再从剩余末排序元素中继续寻找最小(大)元素,然后放到一排序序列的末尾
- 重复第二步,直到所有元素均排序完毕.
代码实现
arr = [1, 23, 4, 56, 7, 87, 0]
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
arr[i], arr[j] = arr[j], arr[i]
print(n) # 7
print(arr) # [0, 1, 4, 7, 23, 56, 87]
插入排序(Insertion Sort)
插入排序是通过构建有序序列,对于未排序数据,在一排序序列中从后向前扫描,找到相应位置并插入.
算法图解
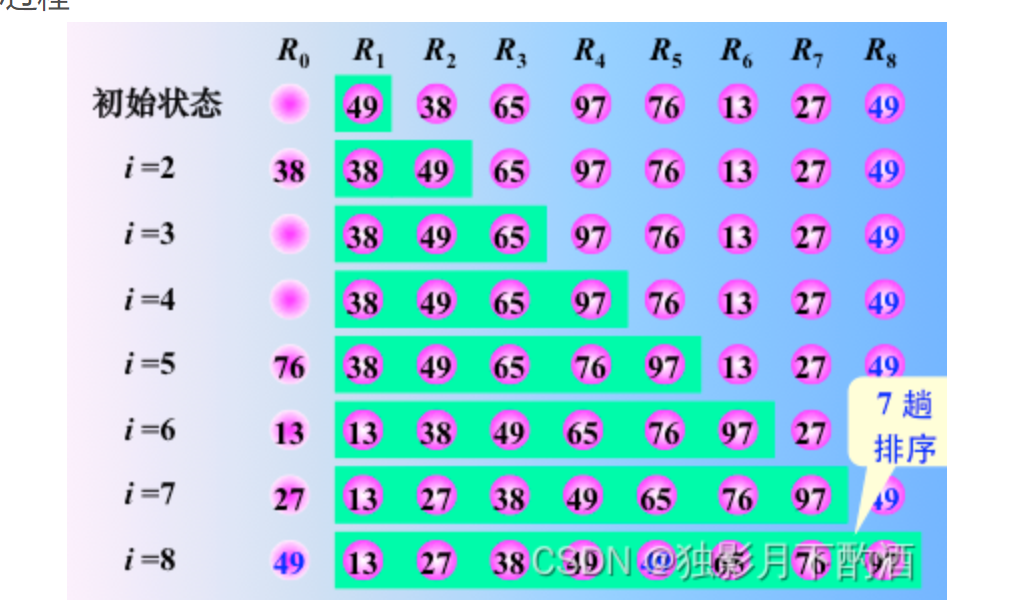
- 将第一个记录看作是有序子序列,然后从第二个记录开始,逐个进行插入,直到整个序列有序.
代码展示
arr = [1, 23, 4, 56, 7, 87, 0]
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
print(n) # 7
print(arr) # [0, 1, 4, 7, 23, 56, 87]
推排序(Heap Sort)
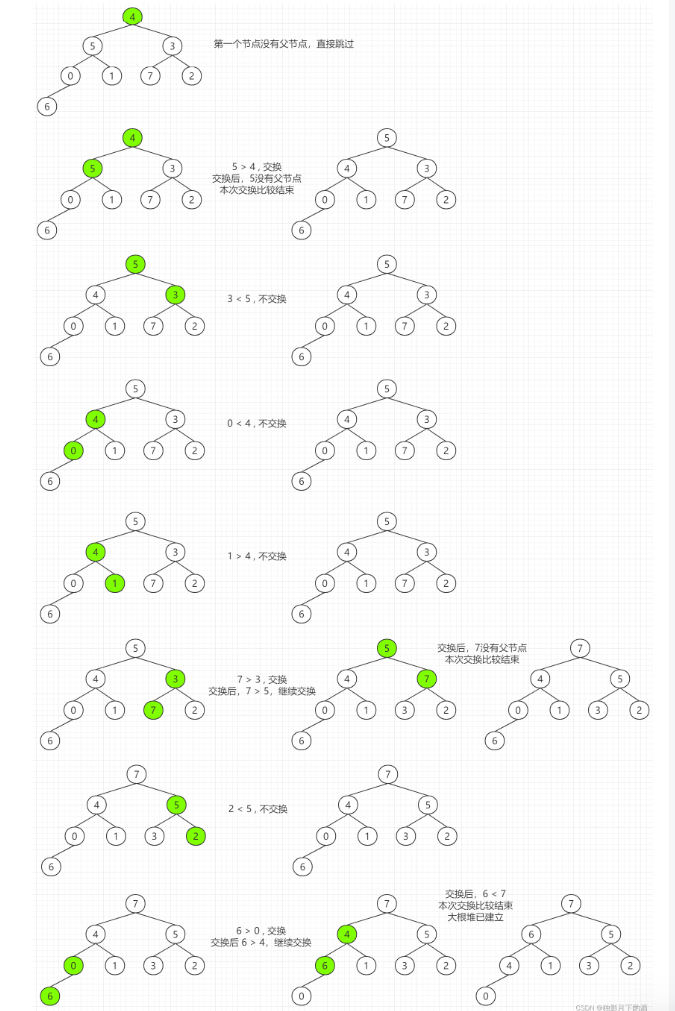
堆算法是利用堆这种数据结构所设计的一种排序算法,堆是一个近似完全二叉树的结构,并同时满足堆的性质,级子节点的值总是小于(大于)它的父节点
大根堆:每个节点的值都大于或等于其子节点的值,用于升序排序
小根堆:每个节点的值都小于或等于其子节点的值,用于降序排序
图解
https://img-blog.csdnimg.cn/b00901d70cb345fcb4e0143fc5279387.gif#pic_center
代码实现
快速排序(Quick Sort)
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr)//2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
归并排序(Merge Sort)
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
result = []
i, j = 0, 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result


 浙公网安备 33010602011771号
浙公网安备 33010602011771号