树的直径

树的直径

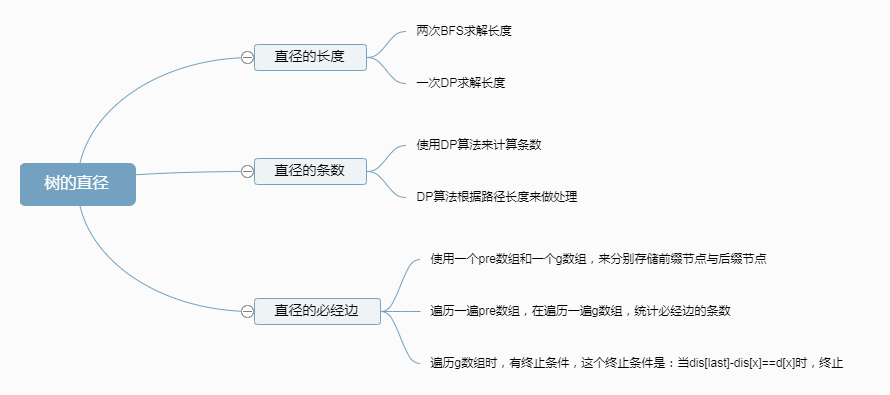
树的直径是一道非常经典的关于树的直径的例题，这道题需要求直径的长度、直径的条数和直径的必经边

直径的长度

直径的长度可以使用一次DP来求解，也可以使用两次BFS来求解

下面给出BFS的求解方法

int bfs(int root){
	int node=root;
	queue<int>q;
	memset(vis,0,sizeof(vis));
	memset(dis,0,sizeof(dis));
	vis[root]=1;
	q.push(root);
	while(q.size()){
		int x=q.front();q.pop();
		vis[x]=1;
		for(int i=head[x];~i;i=e[i].next){
			int y=e[i].to;
			if(vis[y])continue;
			dis[y]=dis[x]+e[i].w;
			vis[y]=1;
			pre[y]=x;
			if(dis[y]>dis[node])node=y;
			q.push(y);
		}
	}
	return node;
}

　　

直径的条数

直径的条数需要使用dp来求解，它使用距离来进行求解，dp执行完后，既可以得到直径的长度，也可以得到直径的条数

下面给出代码

void dp(int x,int fa){
	ll dist=0;
	d[x]=0;node[x]=1;
	for(int i=head[x];~i;i=e[i].next){
		int y=e[i].to;
		if(y==fa)continue;
		dp(y,x);
		dist=d[y]+e[i].w;
		if(dist+d[x]>fx){
			num=node[x]*node[y];
			fx=dist+d[x];
		}else if(dist+d[x]==fx)num+=node[x]*node[y];
		if(d[x]<dist){
			d[x]=dist;
			node[x]=node[y];
		}else if(d[x]==dist)node[x]+=node[y];
	}
}

　　

 

直径的必经边

直径的必经边需要使用一个pre数组和一个g数组，来分别存储前缀节点与后缀节点，先遍历一遍pre数组，再遍历一遍g数组，统计必经边的条数，在遍历g数组时，有终止条件，这个终止条件是：当dis[last]-dis[x]==d[x]时，终止

下面给出代码

void dfs(int x){
	vis[x]=1;
	for(int i=head[x];~i;i=e[i].next){
		int y=e[i].to;
		if(vis[y])continue;
		dfs(y);
		d[x]=max(d[y]+e[i].w,d[x]);
	}
}



for(x=last;x!=-1;x=pre[x])vis[x]=1;
for(x=last;x!=-1;x=pre[x])dfs(x);
L=x;
for(x=last;x!=-1;x=pre[x]){
	g[pre[x]]=x;
	if(dis[x]==d[x]){
		L=x;
		break;
	}
}
for(x=L;x!=last;x=g[x]){
	if(d[x]==dis[last]-dis[x])break;
	ans++;
}

　　

最后给出总的代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5+39+7,M = 4*N;
struct edge{
	ll next,to,w;
}e[M];
ll mp[N],n,head[N],cnt=-1,num=0,fx=0,Max[N],dis[N],vis[N],node[N],pre[N],g[N],d[N],ans=0;
void add(int u,int v,int w){
	e[++cnt]=(edge){head[u],v,w};
	head[u]=cnt;
}
int bfs(int root){
	int node=root;
	queue<int>q;
	memset(vis,0,sizeof(vis));
	memset(dis,0,sizeof(dis));
	vis[root]=1;
	q.push(root);
	while(q.size()){
		int x=q.front();q.pop();
		vis[x]=1;
		for(int i=head[x];~i;i=e[i].next){
			int y=e[i].to;
			if(vis[y])continue;
			dis[y]=dis[x]+e[i].w;
			vis[y]=1;
			pre[y]=x;
			if(dis[y]>dis[node])node=y;
			q.push(y);
		}
	}
	return node;
}
void dfs(int x){
	vis[x]=1;
	for(int i=head[x];~i;i=e[i].next){
		int y=e[i].to;
		if(vis[y])continue;
		dfs(y);
		d[x]=max(d[y]+e[i].w,d[x]);
	}
}
void dp(int x,int fa){
	ll dist=0;
	d[x]=0;node[x]=1;
	for(int i=head[x];~i;i=e[i].next){
		int y=e[i].to;
		if(y==fa)continue;
		dp(y,x);
		dist=d[y]+e[i].w;
		if(dist+d[x]>fx){
			num=node[x]*node[y];
			fx=dist+d[x];
		}else if(dist+d[x]==fx)num+=node[x]*node[y];
		if(d[x]<dist){
			d[x]=dist;
			node[x]=node[y];
		}else if(d[x]==dist)node[x]+=node[y];
	}
}
int main(){
	memset(head,-1,sizeof(head));cnt=-1;
	memset(node,1,sizeof(node));
	memset(pre,-1,sizeof(pre));
	memset(g,-1,sizeof(g));
	cin>>n;
	for(int i=1;i<n;i++){
		ll a,b,c;cin>>a>>b>>c;
		add(a,b,c);
		add(b,a,c);
	}
	ll start=bfs(1);
	ll last=bfs(start);
	int x,L,ans=0;
	pre[start]=-1;
	dp(1,0);
	memset(vis,0,sizeof(vis));
	memset(d,0,sizeof(d));
	for(x=last;x!=-1;x=pre[x])vis[x]=1;
	for(x=last;x!=-1;x=pre[x])dfs(x);
	L=x;
	for(x=last;x!=-1;x=pre[x]){
		g[pre[x]]=x;
		if(dis[x]==d[x]){
			L=x;
			break;
		}
	}
	for(x=L;x!=last;x=g[x]){
		if(d[x]==dis[last]-dis[x])break;
		ans++;
	}
	cout<<fx<<'\n'<<ans<<'\n'<<num;
	return 0;
}