Burnside定理和Polya计数

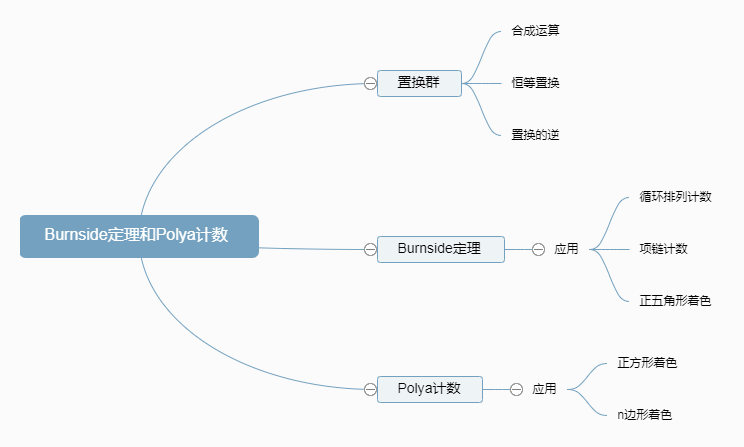
置换群

Burnside定理和Polya计数都需要运用置换群的知识

置换群主要有三种运算，分别是合成运算、恒等置换、置换的逆

运用着三种运算就可以推导出Burnside定理和Polya计数的公式

Burnside定理

Burnside定理的主要应用是循环排列计数、项链计数、正五角形着色等

下面给出一道例题

P1446 [HNOI2008] Cards

通过Burnside定理可以推导出答案(r+g+b)!/(m+1)*r!*g!*b!

 代码：

#include<bits/stdc++.h>
#define ll unsigned long long
using namespace std;
const int N = 2e2+39+7;
ll n,r,g,b,m,P,fac[N];
ll quickPow(ll a,ll b,ll n){
	ll ans=1;
	while(b){
		if(b&1)ans=(ans*a)%n;
		a=(a*a)%n;
		b>>=1;
	}
	return ans;
}
void Solvefac(){
	fac[0]=1;
	for(int i=1;i<=N-10;i++)fac[i]=fac[i-1]*i%P;
}
int main(){
	cin>>r>>b>>g>>m>>P;
	Solvefac();
	cout<<(fac[r+b+g])*(quickPow(fac[r]%P*fac[b]%P*fac[g]%P*(m+1)%P,P-2,P)%P)%P;
	return 0;
}

　　

Polya计数

Polya计数与Burnside定理相似，但求解问题不同，Polya计数主要求解正方形着色与n边形着色问题

下面是一道关于n边形着色的例题

poj1286 Necklace of Beads

非常经典的Polya计数题目，通过旋转与翻转两种操作，分别计算就可以得出答案

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;
ll n;
ll gcd(ll a,ll b){
	if(!b)return a;
	return gcd(b,a%b);
}
int main(){
	while(cin>>n&&n!=-1){
		if(n==0){
			cout<<0<<'\n';
			continue;
		}
		ll ans=0;
		for(ll i=0;i<n;i++)ans+=(ll)pow(3,gcd(n,i));
		if(n%2)ans+=n*(ll)pow(3,n/2+1);
		else{
			ans+=n/2*(ll)pow(3,n/2);
			ans+=n/2*(ll)pow(3,n/2+1);
		}
		cout<<ans/(n*2)<<'\n';
	}
	return 0;
}