容斥原理

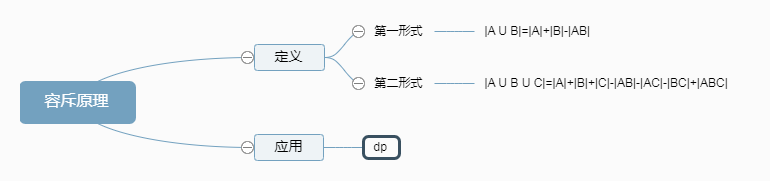
 容斥原理的原式有两个，分别是第一形式：|A U B|=|A|+|B|-|AB|

                                                   第二形式：|A U B U C|=|A|+|B|+|C|-|AB|-|AC|-|BC|+|ABC|

容斥原理最经典的应用是与dp相结合

下面给出一道例题：

P1450 [HAOI2008] 硬币购物

将多重背包与容斥原理相结合，大大提升时间复杂度

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+39+7;
ll dp[N];int c[4],d[4];
int main(){
	for(int i=0;i<4;i++)cin>>c[i];
	dp[0]=1;
	for(int i=0;i<4;i++){
		for(int j=c[i];j<N;j++){
			dp[j]+=dp[j-c[i]];
		}
	}
	int T;cin>>T;
	while(T--){
		for(int i=0;i<4;i++)cin>>d[i];
		int s;cin>>s;
		ll ans=dp[s];
		for(int i=1;i<=15;i++){
			int now=s,tmp=i,opt=0;
			for(int j=0;tmp;j++){
				if(tmp&1)opt^=1,now-=(d[j]+1)*c[j];
				tmp>>=1;
			}
			if(now<0)continue;
			if(opt)ans-=dp[now];
			else ans+=dp[now];
		}
		cout<<ans<<'\n';
	}
	return 0;
}