卢卡斯定理

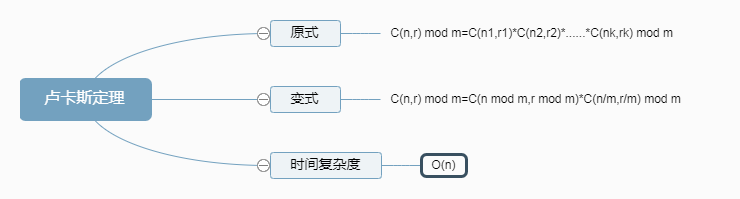
 卢卡斯定理的原式：C(n,r) mod m=C(n1,r1)*C(n2,r2)*......*C(nk,rk) mod m

卢卡斯定理的变式：C(n,r) mod m=C(n mod m,r mod m)*C(n/m,r/m) mod m

卢卡斯定理的时间复杂度很低，接近O(n)

下面给出一道例题

P3807 【模板】卢卡斯定理/Lucas 定理

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+39+7;
ll fac[N];
ll quickPow(ll a,ll n,ll m){
	ll ans=1;
	a%=m;
	while(n){
		if(n&1)ans=(ans*a)%m;
		a=(a*a)%m;
		n>>=1;
	}
	return ans;
}
ll inv(ll a,ll m){return quickPow(fac[a],m-2,m);}
ll c(ll n,ll r,ll m){
	if(r>n)return 0;
	return ((fac[n]*inv(r,m))%m*inv(n-r,m)%m);
}
ll Lucas(ll n,ll r,ll m){
	if(r==0)return 1;
	return c(n%m,r%m,m)*Lucas(n/m,r/m,m)%m;
}
int main(){
	int T;cin>>T;
	while(T--){
		ll a,b,m;cin>>a>>b>>m;
		fac[0]=1;
		for(int i=1;i<=m;i++)fac[i]=(fac[i-1]*i)%m;
		cout<<Lucas(a+b,a,m)<<'\n';
	}
	return 0;
}