鸽巢原理

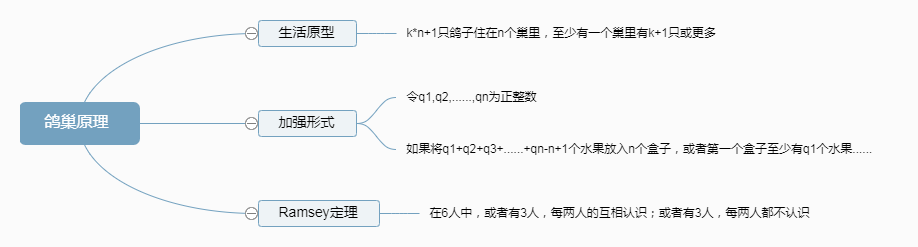
 鸽巢原理的生活原型：k*n+1只鸽子住在n个巢里，至少有一个巢里有k+1只或更多

鸽巢原理的加强形式：令q1,q2,......,qn为正整数，如果将q1+q2+q3+......+qn-n+1个水果放入n个盒子，或者第一个盒子至少有q1个水果......

鸽巢原理的拓展——Ramsey定理：在6人中，或者有3人，每两人的互相认识；或者有3人，每两人都不认识

例题：poj2356

先求前缀和，再求前缀和取余，使用vis数组统计，遍历到2个时输出即可

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#define ll long long
using namespace std;
const int N = 1e4+39+7;
int n,a[N],sum[N],vis[N];
int main(){
	while(cin>>n){
		for(int i=1;i<=n;i++){
			cin>>a[i];
			sum[i]=sum[i-1]+a[i];		
		}
		for(int i=1;i<=n;i++){
			if(sum[i]%n==0){
				cout<<i<<'\n';
				for(int j=1;j<=i;j++)cout<<a[j]<<'\n';
				break;
			}
			if(vis[sum[i]%n]){
				cout<<i-vis[sum[i]%n]<<'\n';
				for(int j=vis[sum[i]%n]+1;j<=i;j++)cout<<a[j]<<'\n';
				break;
			}
			vis[sum[i]%n]=i;
		}
	}
		
	return 0;
}