莫比乌斯函数与反演

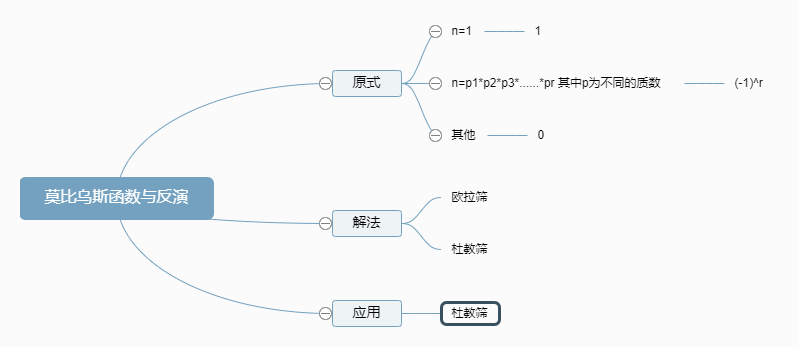
 莫比乌斯函数的原式是u(n)={1,n=1

　　　　　　　　　　　　　(-1)^r,n=p1*p2*p3*......*pr  其中p为不同的质数

                                              0,其他}

它有两种解法，分别是欧拉筛和杜教筛

下面给出欧拉筛的代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+39+7;
bool vis[N];int prime[N],Mob[N];
void Mobius_solve(){
	int cnt=0;
	vis[1]=1;Mob[1]=1;
	for(int i=2;i<N;i++){
		if(!vis[i]){
			prime[cnt++]=i;
			Mob[i]=-1;
		}
		for(int j=0;j<cnt;j++){
			if(prime[j]*i>=N)break;
			vis[prime[j]*i]=1;
			Mob[prime[j]*i]=(i%prime[j]?-Mob[i]:0);
			if(i%prime[j]==0)break;
		}
	} 
}
int main(){
	Mobius_solve();
	int n;cin>>n;
	cout<<Mob[n];
	return 0;
}

　　

杜教筛的代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e6+39+7;
int prime[N],mu[N];ll phi[N];bool vis[N];
unordered_map<int,int>summu;
unordered_map<int,ll>sumphi;
void init(){
	int cnt=0;
	vis[0]=vis[1]=1;
	mu[1]=phi[1]=1;
	for(int i=2;i<N;i++){
		if(!vis[i]){
			prime[cnt++]=i;
			mu[i]=-1;
			phi[i]=i-1;
		}
		for(int j=0;j<cnt&&i*prime[j]<N;j++){
			vis[i*prime[j]]=1;
			if(i%prime[j]){
				mu[i*prime[j]]=-mu[i];
				phi[i*prime[j]]=phi[i]*phi[prime[j]];
			}else{
				mu[i*prime[j]]=0;
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			}
		}
	}
	for(int i=1;i<N;i++){
		mu[i]+=mu[i-1];
		phi[i]+=phi[i-1];
	}
}
int gsum(int x){return x;}
ll getsmu(int x){
	if(x<N)return mu[x];
	if(summu[x])return summu[x];
	ll ans=1;
	for(ll l=2,r;l<=x;l=r+1){
		r=x/(x/l);
		ans-=(gsum(r)-gsum(l-1))*getsmu(x/l);
	}
	return summu[x]=ans/gsum(1);
}
ll getsphi(int x){
	if(x<N)return phi[x];
	if(sumphi[x])return sumphi[x];
	ll ans=x*((ll)x+1)/2;
	for(ll l=2,r;l<=x;l=r+1){
		r=x/(x/l);
		ans-=(gsum(r)-gsum(l-1))*getsphi(x/l);
	}
	return sumphi[x]=ans/gsum(1);
}
int main(){
	init();int T;cin>>T;
	while(T--){
		int n;cin>>n;
		cout<<getsphi(n)<<' '<<getsmu(n)<<'\n';
	}
	return 0;
}