整除分块（数论分块）

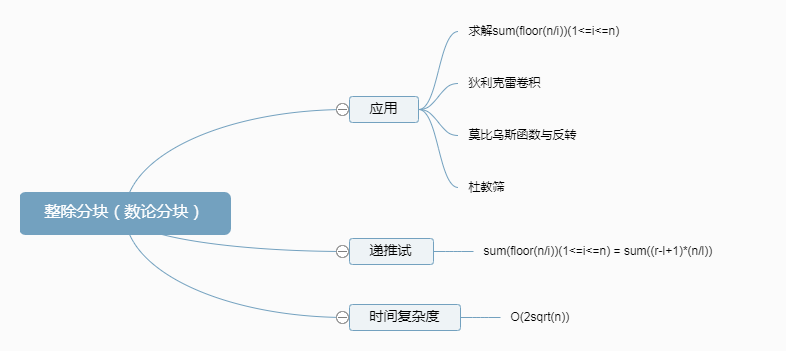
整除分块是为了解决一个整除的求和的问题：sum(floor(n/i))(1<=i<=n)  ，如果直接暴力计算复杂度O（n），但整除分块的复杂度为O（2sqrt(n)），其中的2为常数，可以忽略，那么复杂度为O(sqrt(n))

下面给出整除分块的模板代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,l,r,ans=0;
int main(){
	cin>>n;
	for(l=1;l<=n;l=r+1){
		r=n/(n/l);
		ans+=(r-l+1)*(n/l);
	}	
	cout<<ans;
	return 0;
}

　　

整除分块的主要应用分别是狄利克雷卷积、莫比乌斯函数与反转、杜教筛等