欧拉函数

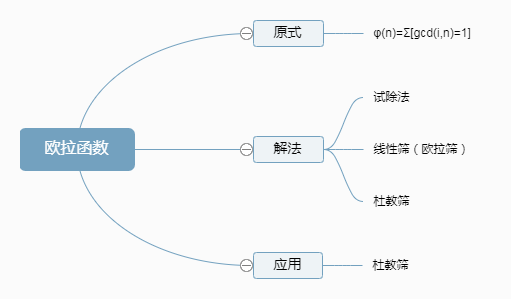
 欧拉函数的原式是φ(n)=Σ[gcd(i,n)=1]，它是一种积性函数，他符合：设p，q是互素的正整数，φ(pq)=φ(p)φ(q)

欧拉函数定理1：设p，q是互素的正整数，φ(pq)=φ(p)φ(q)

欧拉函数定理2：n=Σφ(d)

欧拉函数定理3：φ(n)=nΠ(1-1/p_i)

他最早应用在密码学中

下面给出求法之一试除法的代码，时间复杂度是O(n*sqrt(n))

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int euler(int n){
	int ans=n;
	for(int i=2;i*i<=n;i++){
		if(n%i)continue;
		ans=ans/i*(i-1);
		while(n%i==0)n/=i;
	}
	if(n!=1)ans=ans/n*(n-1);
	return ans;
}
int main(){
	int n;
	cin>>n;
	cout<<euler(n);
	return 0;
}

　　

例题：P2158 [SDOI2008]仪仗队

不妨通过找规律来解题，设C君在坐标（0,0），通过观察，就可以发现当正方形边长为n是，可以看见的人的数量就等于  2*Σφ(i)(2<=i<n)+1 当n=1时，答案为0

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+39+7;
int vis[N],prime[N],euler[N],sum[N];
void get_euler(){
	euler[1]=1;
	int cnt=0;
	for(int i=2;i<N;i++){
		if(!vis[i]){
			vis[i]=i;
			prime[++cnt]=i;
			euler[i]=i-1;
		}
		for(int j=1;j<=cnt;j++){
			if(i*prime[j]>N)break;
			vis[i*prime[j]]=prime[j];
			if(i%prime[j]==0){
				euler[i*prime[j]]=euler[i]*prime[j];
				break;
			}
			euler[i*prime[j]]=euler[i]*euler[prime[j]];
		}
	}
}
int main(){
	get_euler();
	sum[1]=1;
	for(int i=2;i<=N;i++)sum[i]=sum[i-1]+euler[i];
	int n;
	cin>>n;
	if(n==1)cout<<0;
	else cout<<2*sum[n-1]+1;
	return 0;
}

　　

欧拉函数有几个比较常用的应用，比如说杜教筛等

P2158 [SDOI2008] 仪仗