威尔逊定理

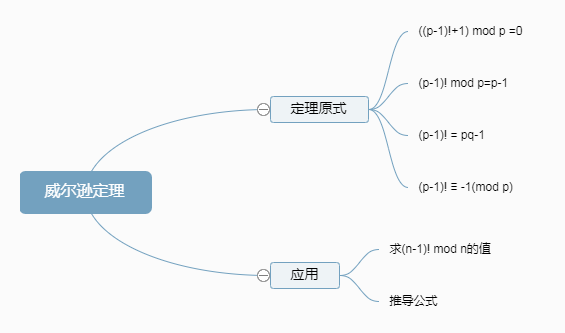
 威尔逊定理：若p为素数，则p可以整除(p-1)!+1

例题1：hdu5391

直接套用威尔逊定理，注意n=4的结果是2

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e9+39+7;
ll quickPow(ll a,ll b,ll m){
	ll ans=1;
	while(b){
		if(b&1)ans=(ans*a)%m;
		a=(a*a)%m;
		b>>=1;
	}
	return ans;
}
bool witness(ll a,ll n){
	ll u=n-1;int t=0;
	while(!(u&1))u>>=1,t++;
	ll x1,x2;
	x1=quickPow(a,u,n);
	for(int i=1;i<=t;i++){
		x2=quickPow(x1,2,n);
		if(x2==1&&x1!=1&&x1!=n-1)return 1;
		x1=x2;
	}
	if(x1!=1)return 1;
	return 0;
}
int Miller_Rabin(ll n,int s){
	srand(time(0));
	if(n<2)return 0;
	if(n==2)return 1;
	if(n%2==0)return 0;
	for(int i=0;i<s&&i<n;i++){
		ll a=rand()%(n-1)+1;
		if(witness(a,n))return 0;
	}
	return 1;
}
int main(){
	int T,n;cin>>T;
	while(T--){
		cin>>n;
		if(n==4)cout<<"2\n";
		else if(Miller_Rabin(n,50))cout<<n-1<<'\n';
		else cout<<0<<'\n';
	}
	return 0;
}

　　

例题2：hdu2973

运用威尔逊定理，推导公式，最终直接计算1到n之间素数的个数即可

代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 4e6+39+7;
bool flag[N];int prime[N],sum[N];
void Prime(int n){
	int cnt=0;
	memset(sum,0,sizeof(sum));
	memset(flag,1,sizeof(flag));
	for(int i=2;i<=n;i++){
		if(flag[i])prime[++cnt]=i;
		for(int j=1;j<=cnt;j++){
			if(i*prime[j]>n)break;
			flag[i*prime[j]]=0;
			if(i%prime[j]==0)break;
		}
	}
}
void init(){for(int i=1;i<=1000000;i++)sum[i]=sum[i-1]+flag[3*i+7];}
int main(){
	ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	Prime(4000000);
	init();	
	int T,n;cin>>T;
	while(T--){
		cin>>n;
		cout<<sum[n];
		if(T)cout<<'\n';
	}
	return 0;
}

　　

例题3：hdu6608

先用米勒测试找到q，在根据威尔逊定理计算。这道题需要用到龟速乘，快速幂，Miller_Rabin测试，费马小定理，非常经典的一道题

代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define ll unsigned long long
using namespace std;
const int N = 1e7+39+7;
ll p,q;
ll quickMul(ll a,ll b,ll m){
	ll ans=0;
	while(b){
		if(b&1)ans=((ans%m)+(a%m))%m;
		a=((a%m)+(a%m))%m;
		b>>=1;
	}
	return ans;
}
ll quickPow(ll a,ll b,ll m){
	ll ans=1;
	while(b){
		if(b&1)ans=quickMul(ans,a,m);
		a=quickMul(a,a,m);
		b>>=1;
	}
	return ans;
}
bool witness(ll a,ll n,ll u,ll t){
	ll x1,x2;
	x1=quickPow(a,u,n);
	for(ll i=1;i<=t;i++){
		x2=quickPow(x1,2,n);
		if(x2==1&&x1!=1&&x1!=n-1)return 1;
		x1=x2;
	}
	if(x1!=1)return 1;
	return 0;
}
bool Miller_Rabin(ll n){
	ll u=n-1,t=0;
	while(!(u&1))u>>=1,t++;
	if(n<2)return 0;
	if(n==2)return 1;
	if(n%2==0)return 0;
	for(ll i=1;i<=50;i++){
		ll a=rand()%(n-1)+1;
		if(witness(a,n,u,t))return 0;
	}
	return 1;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int T;
	cin>>T;
	while(T--){
		ll ans=1;
		cin>>p;ans=p-1;
		q=p-1;
		while(!Miller_Rabin(q))q--;
		for(ll i=q+1;i<=p-1;i++)ans=quickMul(ans,quickPow(i,p-2,p),p);
		cout<<ans<<'\n';
	}	
	return 0;
}