同余

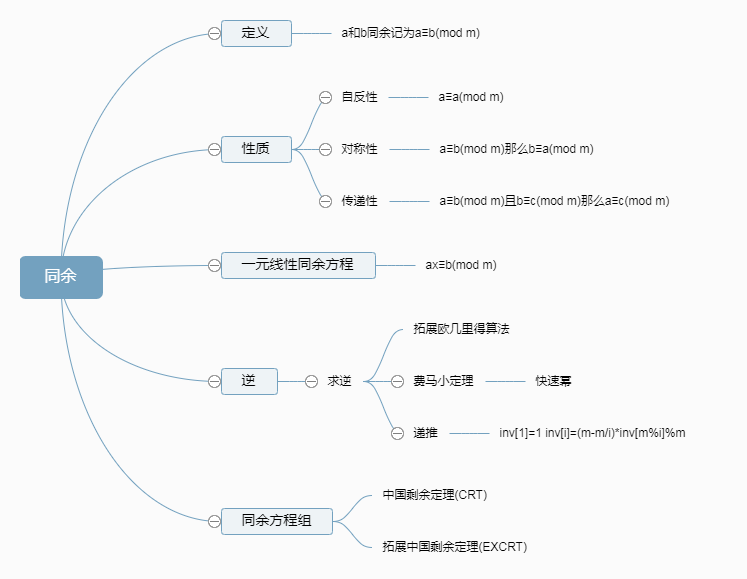
 求逆

例题1：P1082 [NOIP2012 提高组] 同余方程

模板题，使用拓展欧几里得算法求逆

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll gcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;y=0;
		return a;
	}
	ll d=gcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}
ll inverse(ll a,ll m){
	ll x,y;
	gcd(a,m,x,y);
	return (x%m+m)%m;
}
int main(){
	ll a,m;cin>>a>>m;
	cout<<inverse(a,m);
	return 0;
}

　　

例题2：poj2115  C Looooops

使用裴蜀定理判断是否有解，再求逆

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
ll gcd(ll a,ll b){
	if(!b)return a;
	return gcd(b,a%b);
}
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;y=0;
		return a;
	}
	ll d=exgcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}
int main(){
	ll a,b,c,k;
	while(cin>>a>>b>>c>>k){
		if(a==0&&b==0&&c==0&&k==0)break;
		ll B=1LL<<k,x,y;
		exgcd(c,B,x,y);
		if((b-a)%gcd(c,B)==0){
			x*=(b-a)/gcd(c,B);
			ll m=B/gcd(c,B);
			cout<<(x%m+m)%m<<'\n';
		}else cout<<"FOREVER\n";
	}
	return 0;
}

 

例题3：P3811 【模板】乘法逆元

使用递推式 inv[i]=(m-m/i)*inv[m%i]%m来求乘法逆元

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e6+39+7;
ll inv[N];
void inverse(ll n,ll p){
	inv[1]=1;
	for(int i=2;i<=n;i++)inv[i]=(p-p/i)*inv[p%i]%p;
}
int main(){
	ll n,p;cin>>n>>p;
	inverse(n,p);
	for(int i=1;i<=n;i++)cout<<inv[i]<<'\n';
	return 0;
}

　　

例题4：hdu1576  A/B

求逆元，得到k/n，在乘n，得到结果

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;y=0;
		return a;
	}
	ll d=exgcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}
int main(){
	ll n,b,T,x,y;cin>>T;
	while(T--){
		x=y=0;
		cin>>n>>b;
		exgcd(b,9973,x,y);
		x=(x+9973)%9973;
		cout<<x*n%9973<<'\n';
	}
	return 0;
}

　　

例题4：hdu5976  Detachment

使用逆元计算除法取模，再用二分加前缀和与连续积来计算

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+39+7,MOD = 1e9+7;
ll sum[N],mul[N],inv[N];
void init(){
	inv[1]=1;sum[1]=0,mul[1]=1;
	for(int i=2;i<50000;i++){
		sum[i]=sum[i-1]+i;
		mul[i]=(mul[i-1]*i)%MOD;
		inv[i]=(MOD-MOD/i)*inv[MOD%i]%MOD;
	}
}
int main(){
	ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	init();
	int T;cin>>T;
	while(T--){
		int x;cin>>x;
		if(x==1){
			cout<<1<<'\n';
			continue;
		}
		int k=upper_bound(sum+1,sum+50000+1,x)-sum-1;
		int m=x-sum[k];
		if(k==m)cout<<mul[k]*inv[2]%MOD*(k+2)%MOD<<'\n';
		else cout<<mul[k+1]*inv[k-m+1]%MOD<<'\n';
	}
	return 0;
}

　　

中国剩余定理

例题：P4777 【模板】扩展中国剩余定理（EXCRT）

使用迭代法，不断合并方程式，得到答案

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+39+7;
int n;ll ai[N],mi[N];
ll quickMul(ll a,ll b,ll m){
	ll ans=0;
	while(b){
		if(b&1)ans=(ans+a)%m;
		a=(a+a)%m;
		b>>=1;
	}
	return ans;
}
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;y=0;
		return a;
	}
	ll d=exgcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}
ll EXCRT(){
	ll x,y,a1=ai[1],m1=mi[1],ans=0;
	for(int i=2;i<=n;i++){
		ll a2=ai[i],m2=mi[i];
		ll a=m1,b=m2,c=(a2-a1%m2+m2)%m2;
		ll d=exgcd(a,b,x,y);
		if(c%d)return -1;
		x=quickMul(x,c/d,b/d);
		ans=a1+x*m1;
		m1=m2/d*m1;
		ans=(ans%m1+m1)%m1;
		a1=ans;
	}
	return ans;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>mi[i]>>ai[i];
	cout<<EXCRT();
	return 0;
}