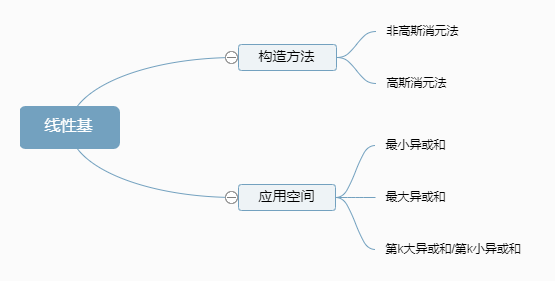
线性基

1.线性基——最大异或和

例题：洛谷P3812

模板题，代码用的是非高斯消元法来构造线性基的

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int M = 63;
long long p[M];
bool zero;
void insert(long long x){
	for(int i=M;i>=0;i--){
		if(x>>i==1){
			if(p[i]==0){
				p[i]=x;
				return;
			} else x^=p[i];
		}
	}
	zero=1;
}
long long qmax(){
	long long ans=0;
	for(int i=M;i>=0;i--)ans=max(ans,ans^p[i]);
	return ans;
}
int main(){
	long long x,n;cin>>n;
	for(int i=1;i<=n;i++)cin>>x,insert(x);
	cout<<qmax();
	return 0;
}

　　

2.线性基——第k大异或和/第k小异或和

例题：hdu3949

模板题

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int N = 1e5+255;
ll n,a[N];
bool zero;
void Gauss(){
    int i,k=1;ll j=(ll)1<<62;
    for(;j;j>>=1){
        for(i=k;i<=n;i++)if(a[i]&j)break;
        if(i>n)continue;
        swap(a[i],a[k]);
        for(int i=1;i<=n;i++)if(i!=k&&a[i]&j)a[i]^=a[k];
        k++;
    }
    k--;
    if(k!=n)zero=1;
    else zero=0;
    n=k;
}
ll query(ll k){
    ll ans=0;
    if(zero)k--;
    if(!k)return 0;
    for(int i=n;i;i--){
        if(k&1)ans^=a[i];
        k>>=1;
    }
    if(k)return -1;
    return ans;
}
int main(){
    int cnt=0,T;cin>>T;
    while(T--){
        printf("Case #%d:\n",++cnt);
        cin>>n;
        for(int i=1;i<=n;i++)cin>>a[i];
        Gauss();
        int q;cin>>q;
        while(q--){
            ll k;cin>>k;
            cout<<query(k)<<'\n';
        }
    }
    return 0;
}