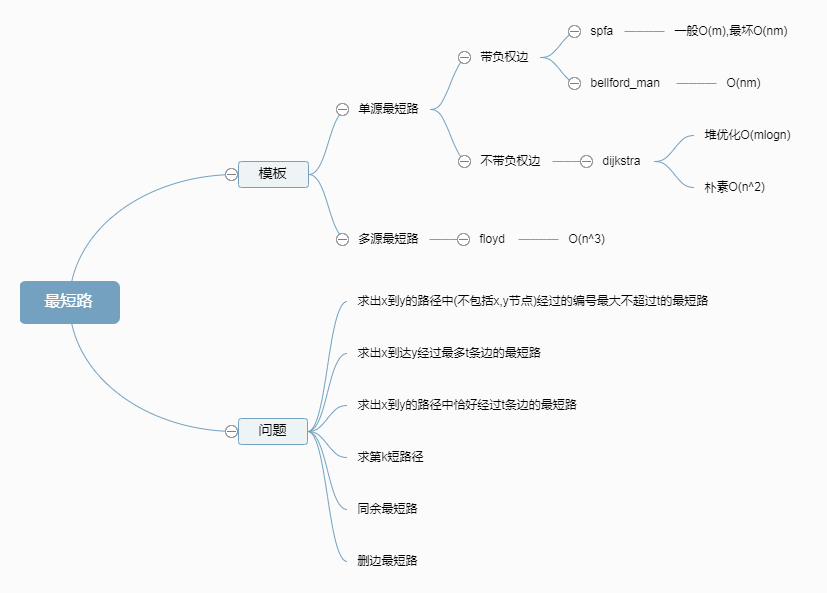
最短路

 

 

 1.朴素dijkstra O(n^2)

int edge[2501][2501],dist[2501],n,m,s,t;
bool flag[2501];
void dijkstra(int u){
	for(int i=1;i<=n;i++){
		dist[i]=edge[u][i];
		flag[i]=false;
	}
	flag[u]=true;
	dist[u]=0;
	for(int i=1;i<=n;i++){
		int temp=INT_MAX,id;
		for(int j=1;j<=n;j++){
			if(!flag[j]&&temp>dist[j]){
				id=j;
				temp=dist[j];
			}
		}
		if(id==u)continue;
		flag[id]=true;
		for(int j=1;j<=n;j++){
			if(!flag[j]){
				dist[j]=min(dist[j],dist[id]+edge[j][id]);
			}
		}
	}
}

2.堆优化dijkstra O(mlogn)

const int N = 1e6+255;
const int M = 1e7+255;
int n,m,s,t,dist[N],tot,head[N];
struct e{
	int to,next,w;
}edge[M];
void add(int u,int v,int w){
	edge[++tot].next=head[u];
	edge[tot].to=v;
	edge[tot].w=w;
	head[u]=tot;
}
void dijkstra(int u){
	priority_queue<pii>q;
	memset(dist,0x3f,sizeof(dist));
	q.push({0,u});
	dist[u]=0;
	while(q.size()){
		int w=q.top().first,id=q.top().second;
		q.pop();
		if(w+dist[id])continue;
		for(int i=head[id];~i;i=edge[i].next){
			int v=edge[i].to;
			if(dist[v]>dist[id]+edge[i].w){
				dist[v]=dist[id]+edge[i].w;
				q.push({-dist[v],v});
			}
		}
	}
}

3.bellman_ford  O(nm)

const int N = 1e5+255;
int dist[N],backup[N],n,m,k;
struct edge{
	int a,b,w;
}e[N];
int bellman_ford(){
	memset(dist,0x3f,sizeof(dist));
	dist[1]=0;
	for(int i=1;i<=k;i++){
		memcpy(backup,dist,sizeof(dist));
		for(int j=1;j<=m;j++){
			int a=e[j].a,b=e[j].b,w=e[j].w;
			dist[b]=min(dist[b],backup[a]+w);
		}
	}
	if(dist[n]>=0x3f3f3f3f/2)return -1;
	else return dist[n];
}

　

4.SPFA  最好O(m)，最坏O(nm)

const int N = 1e5+255;
int dist[N],tot,n,m,head[N];
bool vis[N];
struct edge{
	int to,next,w;
}e[N];
void add(int u,int v,int w){
	e[++tot]={v,head[u],w};
	head[u]=tot;
}
void SPFA(){
	queue<int>q;
	q.push(1);
	memset(dist,0x3f,sizeof(dist));
	dist[1]=0;
	vis[1]=1;
	while(q.size()){
		int x=q.front();
		q.pop();
		vis[x]=0;
		for(int i=head[x];~i;i=e[i].next){
			int y=e[i].to;
			if(dist[y]>dist[x]+e[i].w){
				dist[y]=dist[x]+e[i].w;
				if(!vis[y]){
					q.push(y);
					vis[y]=1;
				}
			}
		}
	}
}

　　

5.floyd O(n^3)

const int N = 2e2+255,INF = 0x3f3f3f3f;
long long d[N][N],edge[N][N],n,m,k,a,b,z;
void floyd(){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			d[i][j]=edge[i][j];
		}
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(d[i][j]>d[i][k]+d[k][j]&&(d[i][k]+d[k][j])<=INF){
					d[i][j]=d[i][k]+d[k][j];
				}
			}
		}
	}
}

 

6.求出x到y的路径中(不包括x,y节点)经过的编号最大不超过t的最短路   Floyd

void Floyd(){
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				DP[k][i][j]=min(DP[k-1][i][j],DP[k-1][i][k]+DP[k-1][k][j]);
			}
		}
	}
}

　　

7.求出x到达y经过最多t条边的最短路+求出x到y的路径中恰好经过t条边的最短路   bellman_ford

void bellmanford(int root,int distA[][N],int distB[][M]){
	for(int i=0;i<=n;i++)distA[root][i]=0;
	distB[root][0]=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			int x=edge[j].x,y=edge[j].y,z=edge[j].z;
			distA[y][i]=min(distA[y][i],min(distA[y][i-1],distA[x][i-1]+z));
			swap(x,y);
			distA[y][i]=min(distA[y][i],min(distA[y][i-1],distA[x][i-1]+z));
		}
	}
	for(int i=1;i<=m;i++){
		for(int j=1;j<=m;j++){
			int x=edge[j].x,y=edge[j].y,z=edge[j].z;
			distB[y][i]=min(distB[y][i],distB[x][i-1]+z);
			swap(x,y);
			distB[y][i]=min(distB[y][i],distB[x][i-1]+z);
		}
	}
}

　　

8.求第k短路径

 

9.同余最短路

例题：洛谷P2371墨墨的等式

这道题运用的是SPFA和同余系的知识

#include<bits/stdc++.h>
using namespace std;
const int N = 5e6+255,M = 10*N;
int head[N],ver[N],edge[M],Next[M],n,m,tot,A[25];
long long L,R,dist[N];
bool vis[N];
queue<int>Q;
void add(int x,int y,int z){
	ver[++tot]=y;
	edge[tot]=z;
	Next[tot]=head[x];
	head[x]=tot;
}
void SPFA(int root){
	memset(dist,0x3f,sizeof(dist));
	memset(vis,0,sizeof(vis));
	dist[root]=0;
	Q.push(root);
	vis[root]=1;
	while(Q.size()){
		int x=Q.front();Q.pop();
		vis[x]=0;
		for(int i=head[x];~i;i=Next[i]){
			int y=ver[i];
			if(dist[y]>dist[x]+edge[i]){
				dist[y]=dist[x]+edge[i];
				if(!vis[y])vis[y]=1,Q.push(y);
			}
		}
	}
}
int main(){
	memset(head,-1,sizeof(head));tot=-1;
	cin>>n>>L>>R;
	for(int i=1;i<=n;i++)cin>>A[i];
	sort(A+1,A+n+1);
	for(int i=0;i<A[1];i++){
		for(int j=2;j<=n;j++){
			add(i,(i+A[j])%A[1],A[j]);
		}
	}
	SPFA(0);
	long long ans=0;
	for(int i=0;i<A[1];i++){
		if(dist[i]<=R){
			long long small=max(0ll,(L-dist[i])/A[1]);
			if(small*A[1]+dist[i]<L)small++;
			long long big=(R-dist[i])/A[1];
			if(big*A[1]+dist[i]>R)big--;
			ans+=big-small+1;
		}
	}
	cout<<ans;
	return 0;
}

　　

 

10.删边最短路　

 

 参考链接：

https://zhuanlan.zhihu.com/p/440889370