Java课后作业

public class EnumTest {

    public static void main(String[] args) {
        Size s=Size.SMALL;
        Size t=Size.LARGE;
        //s和t引用同一个对象？
        System.out.println(s==t);  //
        //是原始数据类型吗？
        System.out.println(s.getClass().isPrimitive());
        //从字符串中转换
        Size u=Size.valueOf("SMALL");
        System.out.println(s==u);  //true
        //列出它的所有值
        for(Size value:Size.values()){
            System.out.println(value);
        }
    }

}
 enum Size{SMALL,MEDIUM,LARGE};

 

运算结果为

 

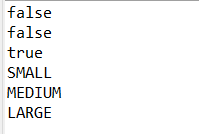
 表明枚举类型的每个具体值指向一个具体对象。

并且可以用"=="或equals()来比较值。

 

原码：​ 原码就是早期用来表示数字的一种方式: 一个正数，转换为二进制位就是这个正数的原码。负数的绝对值转换成二进制位然后在高位补1就是这个负数的原码。

反码：正数的反码就是原码，负数的反码等于原码除符号位以外所有的位取反。

补码：正数的补码与原码相同，负数的补码为 其原码除符号位外所有位取反，然后最低位加1。

例如:

+7的原码:00000111 

-7的原码:10000111

+7的反码:00000111 

-7的反码:11111000

+7的补码:00000111 

-7的补码:11111001

java中采用补码存储数据。

 

public class Test {
    static  int i=10; 
    public static void a() {
        System.out.println(i);
        
    }
    public static void b() {
        int i=1000;
        System.out.println(i);
        
    }
    {
        int i=1001;
        System.out.println(i);

        
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
       int i=100;
       a();
       b();
       System.out.println(i);
       
    }

}

变量作用域中访问遵循就近原则。出了大括号就不认识。

 

 

public class TestDouble {

    public static void main(String args[]) {
        System.out.println("0.05 + 0.01 = " + (0.05 + 0.01));
        System.out.println("1.0 - 0.42 = " + (1.0 - 0.42));
        System.out.println("4.015 * 100 = " + (4.015 * 100));
        System.out.println("123.3 / 100 = " + (123.3 / 100));
    }
}

这表明浮点型在计算机中无法进行精确计算。原因是计算机内部无法用二进制的小数来精确的表达。

 

 

public class TestAdd{
    public static void main(String []args) {
       int X=100;
       int Y=200;
       System.out.println("X+Y="+X+Y);
       System.out.println(X+Y+"=X+Y");
    }
}

 

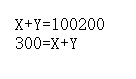
 出现这种结果的原因是第一行输出的第二个加号左边是字符串，因此会做字符串连接自然+Y继续连接。

第二行是因为第一个+两边是操作数。因此会先进行加运算。

 

课后作业

实现30组运算法则题目，避免重复。

public class JiaJianChengChu {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
           int a=0;
           int b=0;
           int i=0;
           int k=0;
           int flag=0;
           int []m =new int [31];
           int []n =new int [31];
          for(i=0;k<30;i++) {
              a=(int)(Math.random()*100+1);
              b=(int)(Math.random()*100+1);
              i=(int)(Math.random()*4+1);
             // k=(int)(Math.random()*4+1);
              switch(i) {
              
              case 1: {
                      if(k==0) {
                          System.out.println(a+"+"+b+"="+(a+b));
                             k++;
                             m[k]=a;
                             n[k]=b;
                             break;
                      }
                      else {  for(int l=0;l<k;l++)
                      {
                          if(m[l]==a&&n[l]==b)
                          {   flag=1;
                              break;
                          }
                          
                      }
                      }
                      if(flag==0) {
                          
                          System.out.println(a+"+"+b+"="+(a+b));
                             k++;
                             m[k]=a;
                             n[k]=b;
                             break;
                      }
                      break;
                    }
              case 2: 
                  {
                      if(k==0) {
                  
                  System.out.println(a+"-"+b+"="+(a-b));
                     k++;
                     m[k]=a;
                  n[k]=b;

                     break;
              }
              else {  for(int l=0;l<k;l++)
              {
                  if(m[l]==a&&n[l]==b)
                  {   flag=1;
                      break;
                  }
                  
              }
              }
              if(flag==0) {
                  
                  System.out.println(a+"-"+b+"="+(a-b));
                     k++;
                     m[k]=a;
                     n[k]=b;
                     break;
               }
                break;   
                  }
            case 3: 
                    {
                        if(k==0) {
                         if(a*b>100) {
                             
                             break;                 
                         }
                         else {
                             System.out.println(a+"*"+b+"="+(a*b));
                             k++;  
                             m[k]=a;
                                n[k]=b;
                            break;
                         }
                        
                    }
                    else {
                        
                         for(int l=0;l<k;l++)
                         {
                             if(m[l]==a&&n[l]==b)
                             {   flag=1;
                                 break;
                             }
                             
                         }
                        if(flag==0) {
                         if(a*b>100) {
                             break;  
                             
                         }
                         else {
                             
                             System.out.println(a+"*"+b+"="+(a*b));
                                k++;
                                m[k]=a;
                                n[k]=b;
                                break;
                             
                         }
                         
                    }
                    }
                  
                                       break;
             
              
              }
              case 4: 
                  
              {
                  if(k==0) {
                  System.out.println(a+"/"+b+"="+(a/b));
                     k++;
                     m[k]=a;
                  n[k]=b;

                     break;
              }
              else {  for(int l=0;l<k;l++)
              {
                  if(m[l]==a&&n[l]==b)
                  {   flag=1;
                      break;
                  }
                  
              }
              }
              if(flag==0) {
                  
                  System.out.println(a+"/"+b+"="+(a/b));
                     k++;
                     m[k]=a;
                     n[k]=b;
                     break;
               }
                break;                            
              
              }
              }
          }
    }

}