Sword B树学习笔记一

概念

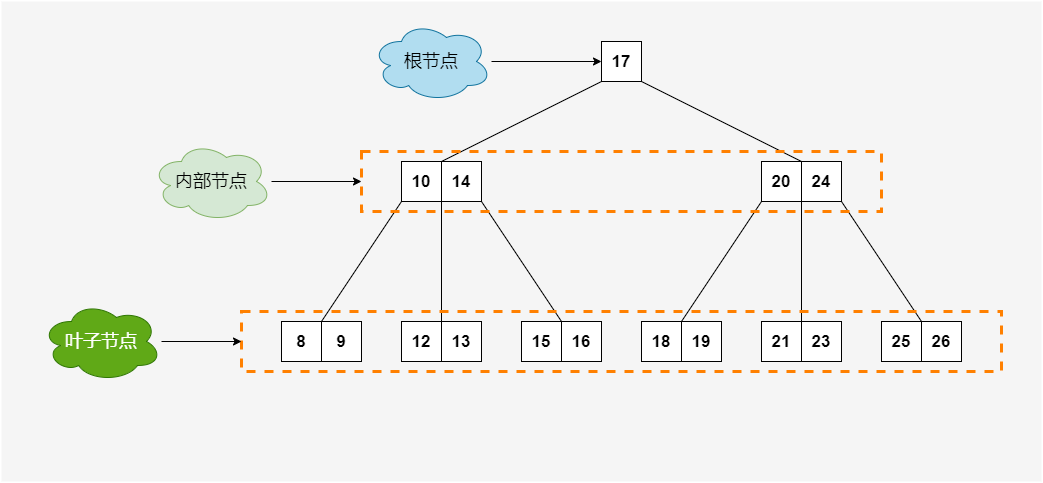
阶（Order）：一个节点可能包含的最大子节点数，即 B树定义中的 M。
内部节点（Internal Node）：除根节点和叶节点外的所有节点。
叶子节点（Leaf Node）：没有子节点的节点。
键（Key）：存储在节点中的值，用于指导搜索过程。
子节点（Child）：节点的直接后代。

特性

a.树中每个结点最多含有M棵子节点；
b.若根结点不是叶子结点，则至少有2棵子树；
c.除根结点之外的所有非叶子结点至少有[M/2]棵子树(ceil(M/2)向上取整)；
d.树中每个结点最多可以有M-1个关键字；
e.树中每个结点至少有M/2-1个关键字(根节点除外)。

实现

查找

B树查找是从根节点开始向下查找（节点内部执行二分查找），如果一直未命中，查找过程直到叶子节点才结束。
因此，最坏情况下 B树的查找时间复杂度为: log2^M

 

插入

插入新数据项，需先执行查找：如果命中则替换原数据项；如果未命中，则找到相应的叶子节点。
当将新数据项存入到节点，可能会导致节点包含的关键字数量超过允许的最大值，因此需要通过分裂来解决上溢问题。

插入示例

这是一棵3阶B树

 

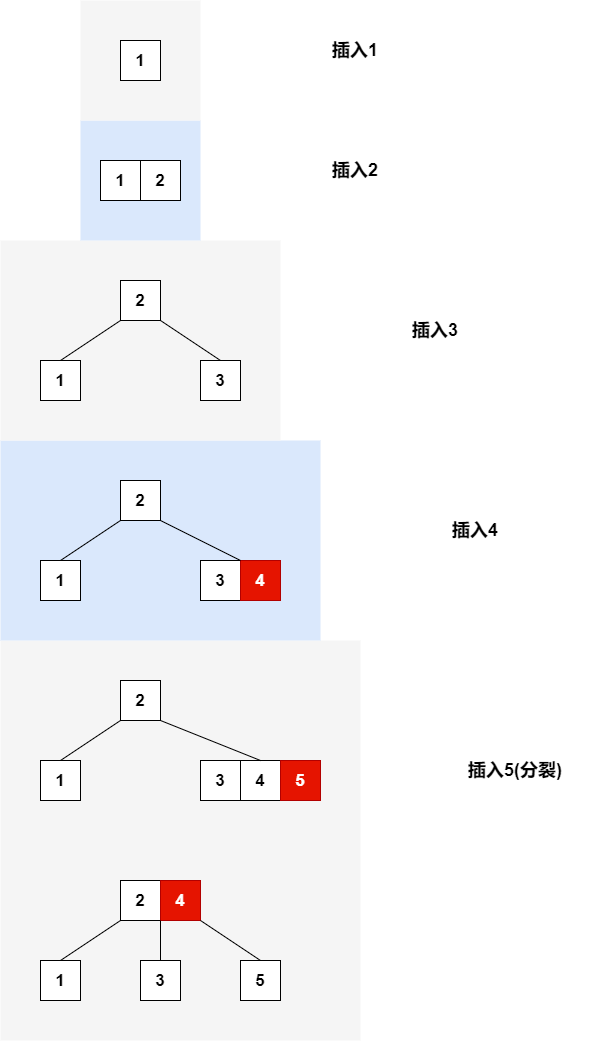
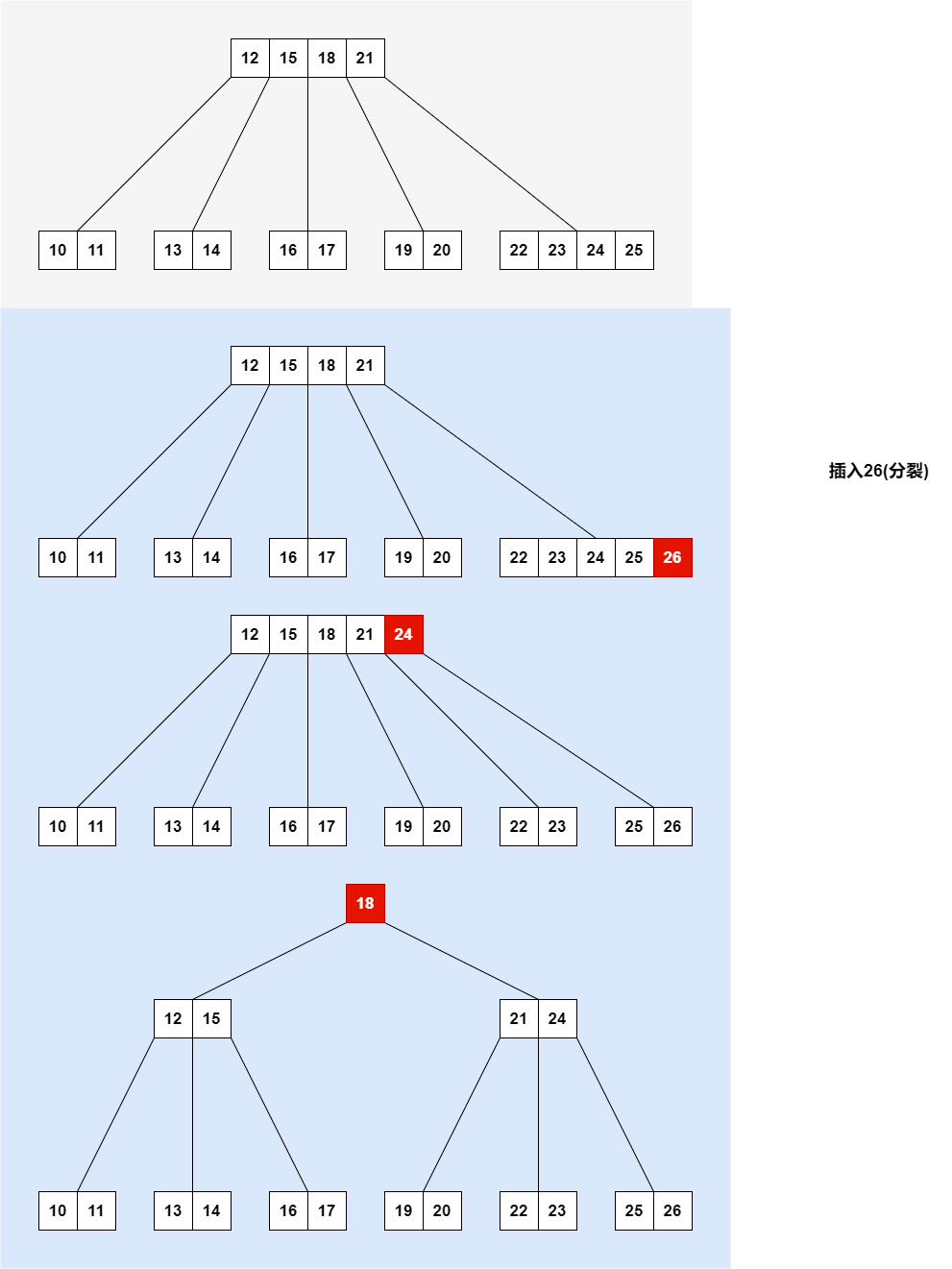
这是一棵5阶B树

对节点[12,15,18,21]进行二分查找，该节点无 26 键且非叶子节点，26 比 21 大进入下一层(21的右孩子)；
对节点[22,23,24,25]进行二分查找，该节点无 26 键且是叶子节点，26 比 25 大，26 保存到 25 的右侧；
节点[22,23,24,25,26]包含的数据项超过最大值4，需处理上溢问题。

提取节点[22,23,24,25,26]的最中间数据项 24 保存到父节点[12,15,18,21]；
以 24 为界将其它数据项分裂成两个子节点 [22,23] 和 [25,26]；
节点[12,15,18,21,24]包含的数据项超过最大值4，需处理上溢问题。

节点[12,15,18,21,24]为根节点，提取节点[12,15,18,21,24]的最中间数据项 18 作为新的根节点，树的高度+1；
以 18 为界将其它数据项分裂成两个子节点[12,15]和[21,24]结束。

删除

这是一棵3阶B树

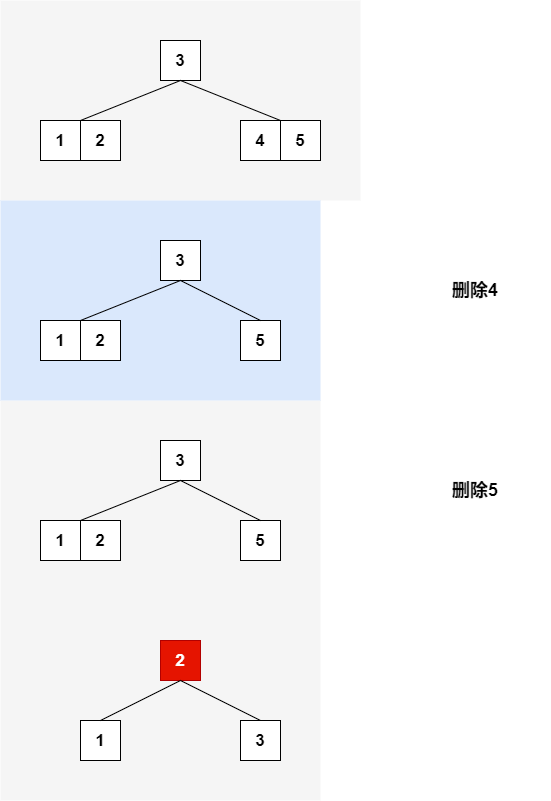
这是一棵5阶B树

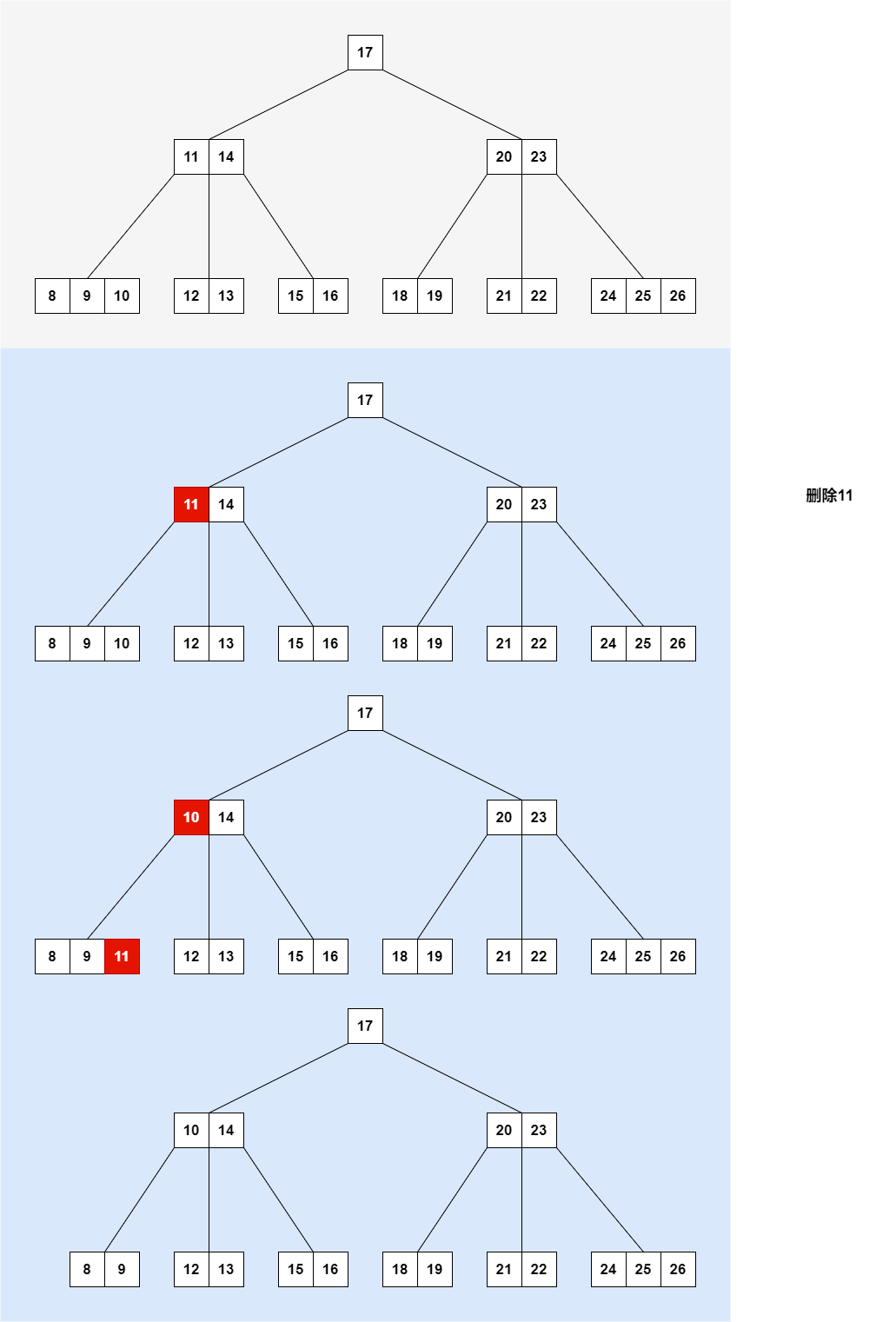
5阶B树删除内部节点中的键

根据键 11 找到节点[11,14]，该节点非叶子节点，判断 11 的左孩子节点[8,9,10]和右孩子节点[12,13]，
发现左孩子节点关键字数量大于右孩子，并且左孩子节点中关键字个数大于2(ceil(5/2)-1)；
因此选择左孩子中的10和当前节点中的11交换；
节点[8,9,11]是叶子节点，删除11；
节点[8,9]关键字数量是2，没有下溢问题，结束。

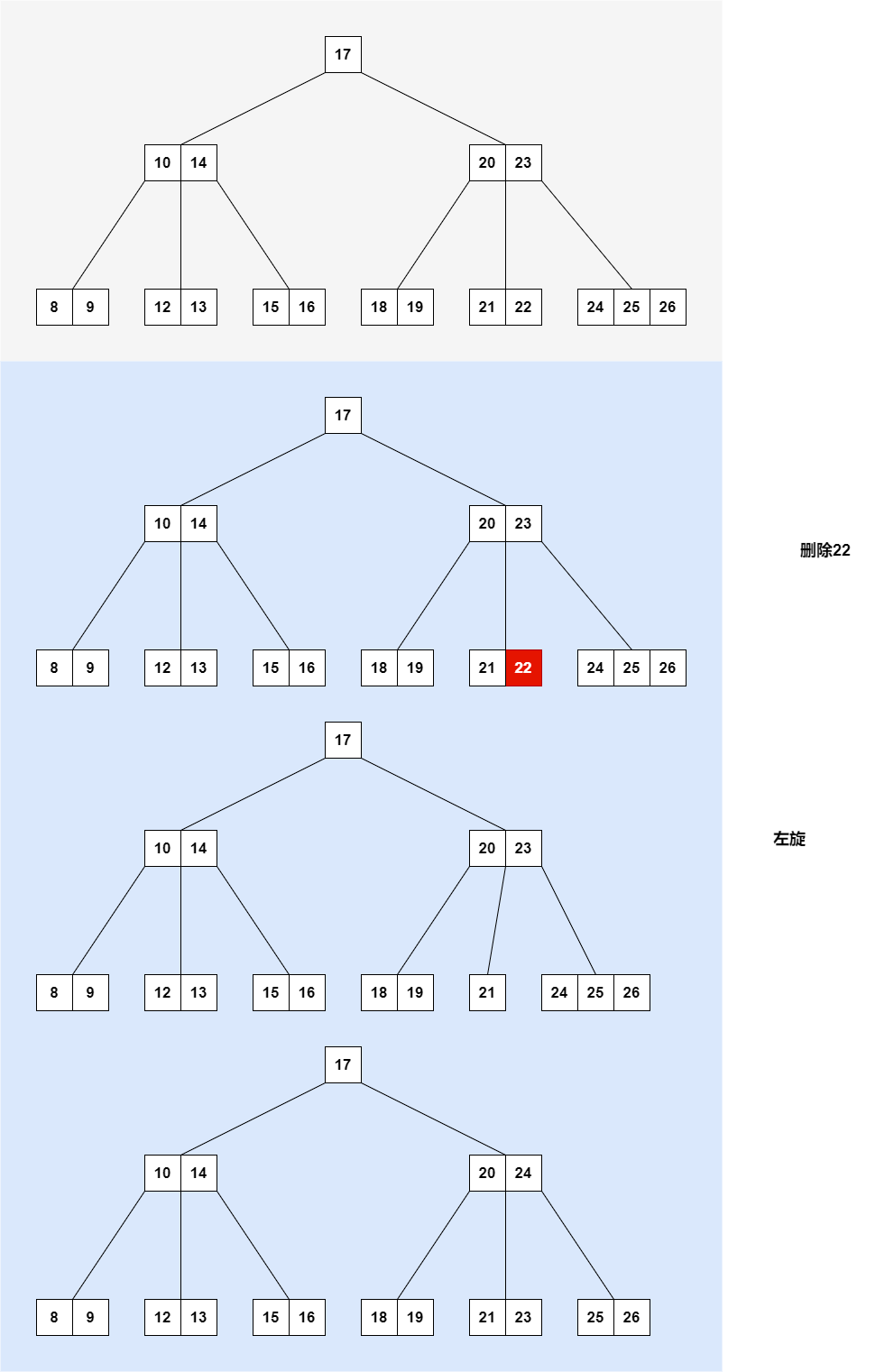
5阶B树删除叶子节点中的键

根据键 22 找到节点 [21,22]，该节点为叶子节点，无需交换，直接删除 22。
删除 22 后节点 [21] 的关键字数量少于2，出现下溢问题；
节点[21]的左兄弟没有富余关键字，右兄弟有富余关键字，因此通过左旋来解决下溢问题；
父节点的 23 移入 [21] 节点，当前节点变成[21，23]，父节点的变成 [20]；
右兄弟节点的 24 移入父节点；父节点的变成[20,24]，右兄弟节点变成[25,26]。

5阶B树删除叶子节点中的键

根据键 23 找到节点[21,23]，该节点为叶子节点，直接删除 23；
删除 23 后节点 [21] 仅余 1 个键，出现下溢问题；
节点[21]的左兄弟和右兄弟均没有富余关键字，因此需要通过合并来解决下溢问题;

父节点[20.24]的 24 移入[21]节点，该节点变成[21,24]，父节点变成[20]；
节点[21,24]和其右兄弟[25,26]合并，合并后变成[21,24,25,26]；
父节点[20]仅余一个键，出现下溢问题。

节点[20]的左兄弟没有富余关键字，因此需要通过合并来解决下溢问题；
父节点的 17 移入节点[20]，节点[20]变成[17,20]；
节点[17,20]与左兄弟[10,14]合并，合并后变成[10,14,17,20]；
父节点已经没有键，且父节点为根节点；
节点[17,20]设为根节点，树的高度减 1。

B树删除
删除操作只能针对叶子节点
如果关键字不是叶子节点，需要根据左孩子或者右孩子关键字的数量选择一个，
将左孩子的最大值(获取右孩子的最小值)和当前节点交换，一直交换到叶子节点为止
删除叶子节点中的关键字可能导致不满足关键字大于M/2-1这个条件，因此需要触发合并，
合并的策略是优先从兄弟节点中借关键字，要是兄弟节点可以借到关键字，那么进行旋转操作，实现B树平衡，
要是兄弟节点借不到关键字，则需要合并兄弟节点，合并兄弟节点的方法是借父节点中的关键字