pytorch学习笔记2
pytorch学习笔记2

|
定义 |
ADAMW优化器 官方手册 构造函数 CLASS torch.optim.AdamW(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0.01, amsgrad=False, *, maximize=False, foreach=None, capturable=False)
|
|
参数 |
Parameters:参数 params (iterable) – iterable of parameters to optimize or dicts defining parameter groups 参数(可迭代的)-将要进行优化的可迭代参数,或者定义参数组的词典 lr (float, optional) – learning rate (default: 1e-3) 学习率(浮点数,可选):-默认值1e-3 betas (Tuple[float, float], optional) – coefficients used for computing running averages of gradient and its square (default: (0.9, 0.999)) β贝塔(两个浮点数组成的元组tuple,可选):用于计算梯度及其平方的运行平均值的系数 eps (float, optional) – term added to the denominator to improve numerical stability (default: 1e-8) eps(浮点)-在分母上增加项以提高数值稳定性 weight_decay (float, optional) – weight decay coefficient (default: 1e-2) 权重衰减系数,默认值0.01 amsgrad (bool, optional) – whether to use the AMSGrad variant of this algorithm from the paper On the Convergence of Adam and Beyond (default: False) 是否使用该算法的AMSGrad变体的收敛方法,默认不使用 maximize (bool, optional) – maximize the params based on the objective, instead of minimizing (default: False) 基于目标来最大化参数,而不是最小化,默认 最小化 foreach (bool, optional) – whether foreach implementation of optimizer is used (default: None) 是否便利优化器的所有实现方式,默认不遍历; capturable (bool, optional) – whether this instance is safe to capture in a CUDA graph. Passing True can impair ungraphed performance, so if you don’t intend to graph capture this instance, leave it False (default: False) 此实例在CUDA图中计算是否安全。传递True降低性能,如果不打算捕获这个实例,就设置为False(默认值); |
|
方法 |
方法: add_param_group(param_group) Add a param group to the Optimizer s param_groups. 将一组参数添加到参数组中; This can be useful when fine tuning a pre-trained network as frozen layers can be made trainable and added to the Optimizer as training progresses. 对模型进行微调时,这个函数很有用,他可以将冻结的层变成可训练的,并且添加到优化器中进行优化; Parameters:参数 param_group (dict) – Specifies what Tensors should be optimized along with group specific optimization options. 参数组(字典格式)-指明优化参数和特定的优化选项; load_state_dict(state_dict)加载状态词典,加载优化器的状态数据; Loads the optimizer state.
Parameters:参数:状态词典,保存优化器状态数据;可以通过state_dict()函数获取; state_dict (dict) – optimizer state. Should be an object returned from a call to state_dict().
state_dict()可以返回优化器的状态词典; Returns the state of the optimizer as a dict.
It contains two entries:它包含两个条目: 1、.状态词典-一个包含优化器状态的词典。其内容用以区分不同的优化器; state - a dict holding current optimization state. Its content differs between optimizer classes. 2、参数组-是一个包含所有参数组的列表,其中每个参数组都是一个词典; param_groups - a list containing all parameter groups where each parameter group is a dict
step(closure=None)[SOURCE]迈步函数:对参数进行一次优化; Performs a single optimization step.
Parameters:参数(可调用的,可选的),一个重新评估模型并返回损失的闭包。 closure (Callable, optional) – A closure that reevaluates the model and returns the loss.
zero_grad(set_to_none=False)梯度清零函数,将所有的优化张量的梯度清零/置零/归零; Sets the gradients of all optimized torch.Tensor s to zero.
Parameters: set_to_none (bool) – instead of setting to zero, set the grads to None. This will in general have lower memory footprint, and can modestly improve performance. However, it changes certain behaviors. For example: 1. When the user tries to access a gradient and perform manual ops on it, a None attribute or a Tensor full of 0s will behave differently. 2. If the user requests zero_grad(set_to_none=True) followed by a backward pass, .grads are guaranteed to be None for params that did not receive a gradient. 3. torch.optim optimizers have a different behavior if the gradient is 0 or None (in one case it does the step with a gradient of 0 and in the other it skips the step altogether). 参数:是将梯度设置为0还是设置为None。将梯度设置为None,可以减少内存占用,并能适当提高性能。 但是,他会改变一些行为,例如: 1、当用户想要访问梯度数据或者对梯度数据进行一些手动操作时,一个全None张量和一个全0张量明显不同; 2、如果用户设置为全None后,就进行反向传播,对于那些没有接收到梯度的参数,其梯度值一定还是None; 当梯度是0,优化器将用0对参数进行优化,如果是None,则直接跳过而不进行优化; |
交叉熵CrossEntropy和负对数似然损失函数NLLLoss的对比
|
CrossEntropy |
如果用CrossEntropy损失函数,则模型的最后输出不需要LogSoftmax,也不需要Softmax; The input is expected to contain the unnormalized logits for each class (which do not need to be positive or sum to 1, in general). 输入不需要归一化,每个元素的数值可正可负,并且不要求其和为1;
|
|
NLLLoss |
如果用NLLLoss损失函数,则模型最后输出需要LogSoftmax; The input given through a forward call is expected to contain log-probabilities of each class.输入应该是概率的对数的形式;也就是说必须在模型的最后经过LogSoftmax;(Softmax负责转换成概率,Log负责转换成对数形式) |
一个Adamw优化器实例
查看代码
([AdamW (
Parameter Group 0
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 1
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 2
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 3
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 4
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 5
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 6
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 7
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 8
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 9
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 10
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 11
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 12
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 13
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 14
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 15
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 16
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 17
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 18
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 19
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 20
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 21
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 22
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 23
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 24
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 25
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 26
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 27
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 28
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 29
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 30
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 31
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 32
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 33
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 34
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 35
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 36
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 37
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 38
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 39
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 40
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 41
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 42
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 43
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 44
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 45
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 46
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 47
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 48
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 49
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 50
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 51
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 52
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 53
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 54
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 55
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 56
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 57
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 58
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 59
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 60
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 61
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 62
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 63
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 64
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 65
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 66
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 67
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 68
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 69
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 70
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 71
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 72
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 73
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 74
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 75
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 76
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 77
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 78
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 79
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 80
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 81
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 82
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 83
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 84
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 85
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 86
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 87
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 88
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 89
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 90
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 91
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 92
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 93
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 94
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 95
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 96
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 97
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 98
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 99
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 100
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 101
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 102
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 103
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 104
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 105
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 106
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 107
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 108
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 109
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 110
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 111
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 112
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 113
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 114
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 115
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 116
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 117
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 118
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 119
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 120
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 121
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 122
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 123
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 124
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 125
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 126
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 127
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 128
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 129
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 130
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 131
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 132
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 133
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 134
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 135
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 136
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 137
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 138
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 139
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 140
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 141
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 142
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 143
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 144
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 145
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 146
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 147
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 148
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 149
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 150
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 151
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 152
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 153
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 154
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 155
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 156
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 157
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 158
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 159
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 160
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 161
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 162
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 163
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 164
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 165
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 166
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 167
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 168
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 169
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 170
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 171
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 172
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 173
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 174
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 175
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 176
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 177
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 178
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 179
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 180
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 181
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 182
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 183
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 184
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 185
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 186
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 187
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 188
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 189
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 190
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 191
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 192
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 193
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 194
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 195
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 196
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 197
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 198
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 199
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 200
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 201
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
Parameter Group 202
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 5e-05
lr: 5.000000000000001e-07
weight_decay: 0.01
Parameter Group 203
amsgrad: False
betas: (0.9, 0.999)
eps: 1e-08
initial_lr: 0.0001
lr: 1.0000000000000002e-06
weight_decay: 0
)],
[{'scheduler': <pycorrector.macbert.lr_scheduler.WarmupExponentialLR object at 0x0000024746727828>, 'interval': 'step'}])
各种维度张量的适用场景 总结
|
0维张量 |
Loss |
|
1维张量 |
Linear |
|
2维张量 |
|
|
3维张量 |
RNN,[100,10000,200]表示sentence_length=100,vocab_size=10000,embedding_size=200; |
|
4维张量 |
CNN,[32,3,28,28]表示batch=32,channel=3,height=28,width=28= |
|
5维张量 |
|
pytorch张量的属性总结
|
t=torch.ones(2,3,4) print(t.size())#torch.Size([2, 3, 4]) print(t.shape)#torch.Size([2, 3, 4]) print(t.dim())#3总的维度个数,这是一个三维张量 print(t.numel())#24元素总个数2*3*4 |
size()和shape等价,其中size()是一个方法要加小括号,shape是一个字段,不用小括号; 要获取指定维度的size信息,可以使用size(1)或者shape[1]二者依然是等价的; dim()获取张量的维度个数; numel=number of elements表示元素总数,相当于size中各个元素的连乘; |
|
t=torch.ones(2,3) print(t.type())#torch.FloatTensor print(type(t))#<class 'torch.Tensor'> print(isinstance(t,torch.FloatTensor))#True |
张量类型检查的3中方法; t.type()可以获取详细的数据类型; type(t)只能获取该变量是一个Tensor类; isinstance可以判定对象是否是某个类的实例; |
|
t=torch.tensor([[1.,2,3], [4,5,6]]) print(t.min())#tensor(1.) 最小值 print(t.max())#tensor(6.) 最大值 print(t.sum())#tensor(21.) 所有元素求和 print(t.mean())#tensor(3.5000) 所有元素求平均值 t必须是浮点型 print(t.prod())#tensor(720.) 所有元素连乘的积 print(t.argmax())#tensor(5) 最大元素的索引(展平成1维) print(t.argmin())#tensor(0) 最小元素的索引(展平成1维) |
如果不指明维度信息,则是对所有元素进行统计计算; argmax、argmin首先将输入张量展平成1维,然后输出最大值或者最小值的索引号; 所有的返回值都是以张量的形式进行返回,而不是具体的数值; 如果要从0维张量中获取具体数值,可以使用item函数; prod()是product的简写,把张量中每个元素乘起来;
|
|
t=torch.tensor([[1.,2,3], [4,5,6]]) print(t.min(dim=0,keepdim=True)) print(t.max(dim=0,keepdim=True)) print(t.sum(dim=0,keepdim=True)) print(t.mean(dim=0,keepdim=True)) print(t.prod(dim=0,keepdim=True)) print(t.argmax(dim=0,keepdim=True)) print(t.argmin(dim=0,keepdim=True)) 对哪个维度进行统计操作,哪个维度就会消失; keepdim=True则返回值的维度和输入维度相同; keepdim=False,则被统计的维度将会消失; |
torch.return_types.min( values=tensor([[1., 2., 3.]]), indices=tensor([[0, 0, 0]])) torch.return_types.max( values=tensor([[4., 5., 6.]]), indices=tensor([[1, 1, 1]])) tensor([[5., 7., 9.]])#sum求和 tensor([[2.5000, 3.5000, 4.5000]])#mean平均 tensor([[ 4., 10., 18.]])#prod连乘 tensor([[1, 1, 1]])#argmax最大元素的索引 tensor([[0, 0, 0]])#argmin最小元素的索引 |
|
a = torch.full([8], 1.) b = a.view(2, 4) c = a.view(2, 2, 2) print(a.norm(1), b.norm(1), c.norm(1)) # tensor(8.) tensor(8.) tensor(8.) print(a.norm(2), b.norm(2), c.norm(2)) # tensor(2.8284) tensor(2.8284) tensor(2.8284) print(a.norm(1, dim=0), b.norm(1, dim=0), c.norm(1, dim=0)) # tensor(8.) tensor([2., 2., 2., 2.]) tensor([[2., 2.],[2., 2.]]) print(a.norm(2, dim=0), b.norm(2, dim=0), c.norm(2, dim=0)) # tensor(2.8284) tensor([1.4142, 1.4142, 1.4142, 1.4142]) # tensor([[1.4142, 1.4142], [1.4142, 1.4142]]) print(a.norm(1, dim=0,keepdim=True), b.norm(1, dim=0,keepdim=True), c.norm(1, dim=0,keepdim=True)) # ensor([8.]) tensor([[2., 2., 2., 2.]]) # tensor([[[2., 2.], [2., 2.]]]) print(a.norm(2, dim=0,keepdim=True), b.norm(2, dim=0,keepdim=True), c.norm(2, dim=0,keepdim=True)) # tensor([2.8284]) tensor([[1.4142, 1.4142, 1.4142, 1.4142]]) # tensor([[[1.4142, 1.4142], [1.4142, 1.4142]]]) |
# 输入必须维浮点型张量,否则报错 L1 Regularization Term (权值的绝对值求和): L2 Regularization Term(权值的平方求和,再开方): 加上正则化后,要求目标函数的cost要小,权值的绝对值或者平方也要小; 加上L1就可以产生一个稀疏的解; 第一个参数=1就表示是L1正则化; 第一个参数=2就表示是L2正则化; dim表示要统计计算的维度; 如果省略dim,就表示对所有元素进行统计操作; dim=0表示对第0维进行正则化计算; dim=1表示对第1维进行正则化计算; keepdim=True表示返回值的维数和输入的维数相同; keepdim=False表示返回值中将删除统计计算的维度dim; 对哪个维度进行统计,哪个维度就会消失;
|
|
t=torch.tensor([[1,2,3],[4,5,6],[7,8,9]]) print(t.topk(2)) #不指定dim 默认按照dim=-1进行统计 # torch.return_types.topk( # values=tensor([[3, 2],[6, 5],[9, 8]]), # indices=tensor([[2, 1],[2, 1],[2, 1]])) print(t.topk(2,dim=0)) # values=tensor([[7, 8, 9],[4, 5, 6]]), # indices=tensor([[2, 2, 2],[1, 1, 1]])) print(t.topk(2,dim=0,largest=False)) # torch.return_types.topk( # values=tensor([[1, 2, 3],[4, 5, 6]]), # indices=tensor([[0, 0, 0],[1, 1, 1]])) |
topk不仅返回统计的数值,同时还会返回对应的索引; k表示要选取的个数; k=2表示选取最大的和第二大的; dim表示要进行统计的维度; dim如果不指定,默认使用最后一个维度-1; largest=False表示从小的开始取; largest不指定,则默认从大的开始取; |
pytorch创建张量总结
|
torch.full([2,3],7) tensor([[7, 7, 7], [7, 7, 7]]) torch.full([2,3],7.) tensor([[7., 7., 7.], [7., 7., 7.]]) |
创建所有元素相同的LongTensor张量,通过[]指定张量形状; 如果指定数据为浮点型,则创建FloatTensor; 如果指定数据为整形,则创建LongTensor; |
|
torch.arange(1,10) tensor([1, 2, 3, 4, 5, 6, 7, 8, 9]) torch.arange(1.,10.) tensor([1., 2., 3., 4., 5., 6., 7., 8., 9.]) |
前闭后开,创建连续整形张量; 如果指定数据为浮点型,则创建FloatTensor; 如果指定数据为整形,则创建LongTensor; 所有数据均位于[start,end)区间内; |
|
torch.range(1,10) tensor([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]) |
前闭后闭,创建连续浮点型张量; 因为不符合前闭后开的规则,所以range函数被弃用; UserWarning: torch.range is deprecated(弃用的) and will be removed in a future release deprecated - 已弃用 英[ˈdeprəkeɪtɪd]美[ˈdeprəkeɪtɪd]v. 对…表示极不赞成; 强烈反对; |
|
torch.ones(2,3) tensor([[1., 1., 1.],[1., 1., 1.]]) |
创建全为1的浮点型张量FloatTensor; |
|
torch.zeros(2,3) tensor([[0., 0., 0.], [0., 0., 0.]]) |
创建全为0的浮点型张量FloatTensor; |
|
torch.eye(2,3) tensor([[1., 0., 0.], [0., 1., 0.]]) |
创建主对角线全为1,其余元素全为0的浮点型张量FloatTensor; |
|
torch.rand(2,3) tensor([[0.1444, 0.6375, 0.1127], [0.1982, 0.6524, 0.5708]]) |
创建一个浮点型张量FloatTensor; 所有元素都是0-1之间的浮点数,符合平均分布; |
|
torch.randn(2,3) tensor([[ 0.6668, -0.4443, 1.6765], [-1.6271, 0.4040, -1.3142]]) |
创建一个浮点型张量FloatTensor; 所有元素都是0-1之间的浮点数,符合标准正态分布; 0-1分布:标准值为0,标准差为1的正态分布; |
|
torch.randint(1,5,(2,3)) tensor([[3, 2, 4], [2, 4, 2]]) |
创建长整形张量LongTensor;三个参数分别为start,end,size; 所有元素的值位于[start,end)区间内; |
|
torch.empty(2,2) tensor([[9.2755e-39, 8.4490e-39], [1.1112e-38, 9.5511e-39]]) |
创建浮点型张量FloatTensor; 所有元素的值均为未初始化的随机值; 未初始化的张量必须要初始化之后,才能使用; |
|
torch.Tensor(2,2)
|
创建浮点型张量FloatTensor; 所有元素的值均为未初始化的随机值; 未初始化的张量必须要初始化之后,才能使用; |
|
t=torch.IntTensor(2,3);int32 t=torch.LongTensor(2,3); t=torch.ShortTensor(2,3);int16 t=torch.ByteTensor(2,3);uint8 t=torch.FloatTensor(2,3); t=torch.DoubleTensor(2,3);float64 |
根据数据类型创建张量; 所有元素的值均为未初始化的随机值; 未初始化的张量必须要初始化之后,才能使用; |
|
torch.tensor([1,2,3,4,5]) tensor([1, 2, 3, 4, 5]) torch.tensor([1.,2,3,4,5]) tensor([1., 2., 3., 4., 5.]) |
从列表创建张量; 如果列表中的字面量全是整形,则创建整形张量LongTensor; 如果列表中有浮点型字面量,则创建浮点型张量FloatTensor; |
|
a=numpy.array([1,2,3,4,5]) t=torch.from_numpy(a) tensor([1, 2, 3, 4, 5], dtype=torch.int32) a=numpy.array([1.,2,3,4,5]) t=torch.from_numpy(a) # tensor([1., 2., 3., 4., 5.], dtype=torch.float64) |
从numpy创建张量; 如果numpy中的字面量全是整形,则创建整形张量IntTensor; 如果numpy中有浮点型字面量,则创建浮点型张量DoubleTensor; |
|
|
pytorch维度变换总结
|
view改变数据的形状 |
只改变数据的外观,不改变内存结构; view只适合对满足连续性条件(contiguous)的tensor进行操作,而reshape同时还可以对不满足连续性条件的tensor进行操作,具有更好的鲁棒性。 |
|
reshape改变数据的形状 |
view能干的reshape都能干,如果view不能干就可以用reshape来处理。 |
|
squeeze挤压维度 |
挤压掉长度为1的维度; suqeeze(0)表示挤压掉第0个维度; 如果被挤压的维度的长度不是1,则无法挤压,并返回原张量; suqeeze(-1)表示加压最后一个维度(倒数第一个); 参数dim的取值范围是[0,ndim)前闭后开; |
|
unsqueeze增加维度 |
扩张维度,并且扩张后的维度的长度为1; unsqueeze(0)表示在第0个维度左侧扩张一个维度;[2,3]→[1,2,3] unsqueeze(-1)表示在最后一个维度的右侧扩张一个维度;[2,3]→[2,3,1] 参数dim取值范围是[-(ndim+1),ndim+1)前闭后开; |
|
transpose对任意两个维度进行转置; transpose只能交换两个维度 |
torch.transpose(a,1,2) torch.transpose(input, dim0, dim1) → Tensor
|
|
t只能对二维矩阵进行转置 |
torch.t(input) → Tensor 输入维度不能超过2;否则报错; 如果输入为2维,则交换第0和第1维,等价于transpose(input,0,1); 如果输入是1维,则输出结果不变; |
|
permute转置,同时交换任意多个维度 |
permute(0,1,2) # 不改变维度;这是正常顺序; permute(0,2,1) # 交换第1维和第2维; permute(1,0,2)交换第0维和第1维; |
|
expand扩张(广播机制) 不增加内存(推荐); |
拷贝数据和元数据共享同一块内存; 只是拷贝了数据的指针,而没有创建数据本身的副本;
|
|
repeat在指定维度上拷贝多少份; 内存消耗更大; |
拷贝多份,放置在不同的内存区域; t=torch.rand(1,2,3,4) res=t.repeat(5,6,7,8) torch.Size([5, 12, 21, 32]) [1*5,2*6,3*7,4*8]→[5, 12, 21, 32] |
切片和索引 归纳总结
|
概述 |
start:end:step start,end,step都可以省略,这种情况下就使用默认值; 默认值start=0;end=len;step=1;其中len表示该维度上的长度(元素个数); 第二个冒号:可以和step一同省略,此时使用默认值:step=1; 第一个冒号不可省略; |
|
举例 |
[start:end]前闭后开区间,包含start但是不包含end; [0::2]表示所有偶数索引,start=0,end=len(默认),step=2; [1::2]表示所有奇数索引,start=1,end=len(默认),step=2; [:]取所有,start=0,end=len,step=1全部取默认值; [::2]表示所有偶数索引,其中start,end省略,取默认值0和len,而step=2;
[:2,::2,:7:3,3::2]多个维度同时切片,各维度之间用逗号隔开; [...]等价[:,:,:,:]表示所有维度上都是取所有元素; [0,...]等价于[0]表示第一个维度取第0个元素,其余维度取所有; [...,::2]等价于[:,:,:,::2]表示在最后一个维度取偶数索引,其余维度都取所有; [:,1,...]等价于[:,1,:,:]在第二个维度取索引为1的元素,其余维度取所有; [...,:2]等价于[:,:,:,:2]在第二个维度取索引为1的元素,其余维度取所有;
|
各种选取方法总结
|
index_select按照索引进行选取; |
index_select(2,torch.LongTensor([0,3,5]))表示在第二个维度上,分别选取索引号为0,3,5的项;
|
|
masked_select按照掩码选取;掩码size需要和源张量size相同,将选取mask中元素值为1的,在x中相同位置的元素; |
x = torch.randn([3, 4])print(x)# 将x中的每一个元素与0.5进行比较# 当元素大于等于0.5返回True,否则返回Falsemask = x.ge(0.5)print(mask)print(torch.masked_select(x, mask)) |
|
take将原张量打平为一维张量,然后按照索引选取对应元素; |
src = torch.tensor([[4, 3, 5], [6, 7, 8]]) torch.take(src, torch.tensor([0, 2, 5])) tensor([ 4, 5, 8]) |
tensor.equal、eq、ge、gt、le、lt、ne、sort、topk、kthvalue、isfinite、isinf、isnan总结归纳
|
equal,比较shape和所有值是否都相同; 完全相同则只返回一个True; 只要有一个不同,就返回一个False; |
torch.equal(t1,t2);torch.eq(t1,t2); 只返回一个值False |
|
eq两个张量的size必须完全相同(否则报错); 分别比较每个元素,并返回一个同size的张量; 元素相等的,对应返回值就是就是True,否则False; |
t1.equal(t2);t1.eq(t2); 返回一个张量tensor([False, False, False, False]) |
|
ge=greate or equal大于等于、 gt=great than大于、 le=less or equal小于等于、 lt=less than小于 返回一个张量,张量中对应位置元素数值相比; |
t1=torch.LongTensor([1,5,8,4]) t2=torch.LongTensor([2,3,9,1]) print('ge=',torch.ge(t1,t2)) print('ge=',t1.ge(t2)) # ge= tensor([False, True, False, True]) # ge= tensor([False, True, False, True]) |
|
ne=not equal不等于 |
ne= tensor([True, True, True, True]) ne= tensor([True, True, True, True]) |
|
topk按照指定维度,取最大的k个, 最后返回一个张量,和张量中对应元素在原张量中的索引; 如果按照行取k,则返回其中的k行; 如果按照列取,则返回其中的k列; 返回的value张量和index张量的size相同,元素一一对应;
|
t3=torch.LongTensor([[6,8,1,5], [3,6,2,8], [4,2,9,1]]) #按照行对比,取最大的k个 print(torch.topk(t3,k=2,dim=0)) #按照列对比,取最大的k个 print(torch.topk(t3,k=2,dim=1)) |
|
kthvalue 相当于对原张量按照指定维度进行排序(升序); 然后在排序后的张量中取第k行或列; 这里的k不是最大的k而是从最小的开始的k; k=1表示最小的,k=2表示第二小的; dim表示指定的维度; |
a = torch.tensor([ [2, 4, 3, 1, 5], [2, 3, 5, 1, 4]]) print('a\n', a) # 此处的k 的下标是从1开始的不是0开始的 # 从打印结果来看,说明打印出来的,排好序后的第二行数据 print(torch.kthvalue(a, k=2, dim=0))
# 打印出来排好序(升序)的第二列数据 print(torch.kthvalue(a, k=2, dim=1)) # 打印出来排好序(升序)的第一列数据 print(torch.kthvalue(a, k=1, dim=1))
|
|
isfinite无穷数返回False,否则返回True; isinf无穷数返回True,否则返回False; isnan数字返回False,非数字返回True; |
t=torch.Tensor([1,numpy.nan,float('-inf'),float('inf')]) print('t is finite(有限的)=',t.isfinite(),torch.isfinite(t)) print('t is isinf(无穷的)=',t.isinf(),torch.isinf(t)) print('t is nan(非数字的)=',t.isnan(),torch.isnan(t)) |
比较测试
t=torch.Tensor([1,numpy.nan,float('-inf'),float('inf')])
print('t is finite(有限的)=',t.isfinite(),torch.isfinite(t))
print('t is isinf(无穷的)=',t.isinf(),torch.isinf(t))
print('t is nan(非数字的)=',t.isnan(),torch.isnan(t))
# t1=torch.LongTensor([1,5,8,4])
# t2=torch.LongTensor([2,3,9,1])
# t3=torch.LongTensor([[6,8,1,5],
# [3,6,2,8],
# [4,2,9,1]])
# #按照行对比,取最大的k个
# print(torch.topk(t3,k=2,dim=0))
# #按照列对比,取最大的k个
# print(torch.topk(t3,k=2,dim=1))
# torch.return_types.topk(
# values=tensor([[6, 8, 9, 8],
# [4, 6, 2, 5]]),
# indices=tensor([[0, 0, 2, 1],
# [2, 1, 1, 0]]))
# torch.return_types.topk(
# values=tensor([[8, 6],
# [8, 6],
# [9, 4]]),
# indices=tensor([[1, 0],
# [3, 1],
# [2, 0]]))
# print('ne=',torch.ne(t1,t2))
# print('ne=',t1.ne(t2))
# ne= tensor([True, True, True, True])
# ne= tensor([True, True, True, True])
# print('ge=',torch.ge(t1,t2))
# print('ge=',t1.ge(t2))
# # ge= tensor([False, True, False, True])
# # ge= tensor([False, True, False, True])
# print('equal=',torch.equal(t1,t11))
# print('equal=',torch.eq(t1,t2))
# # print('equal=',torch.eq(t1,t12))
# # eq的两个张量的size必须完全相同
# #RuntimeError: The size of tensor a (4) must match the size of tensor b (5) at non-singleton dimension 0
# print('equal=',t1.eq(t2))
# # equal= False
# # equal= tensor([False, False, False, False])
# # equal= tensor([False, False, False, False])张量乘法测试
#张量乘法测试
# a=torch.ones((2,3,2),dtype=torch.int64)
# a[1]=2
# print(a)
# b=torch.randint(0,3,(2,3))#randint数据类型实际是int64,也就是long,而不是int32
# print(b)
# c=a@b
# print(c)
# print('a.size=',a.size(),',b.size=',b.size(),',c.size=',c.size())
# tensor([[[1, 1],
# [1, 1],
# [1, 1]],
#
# [[2, 2],
# [2, 2],
# [2, 2]]])
# tensor([[0, 1, 1],
# [2, 0, 2]])
# tensor([[[2, 1, 3],
# [2, 1, 3],
# [2, 1, 3]],
#
# [[4, 2, 6],
# [4, 2, 6],
# [4, 2, 6]]])
# 由此可见:
# [2, 3, 2]可以分成2个[ 3, 2]张量,
# 然后分别与[2, 3]张量相乘,得到2个[3, 3]张量,
# 最后再把2个[3, 3]拼接起来,形成最终的输出,也就是[2, 3, 3]
a=torch.ones((2,3,2),dtype=torch.int64)
a[1]=2
print(a)
b=torch.randint(0,3,(2,2,3))#randint数据类型实际是int64,也就是long,而不是int32
print(b)
c=a@b
print(c)
print('a.size=',a.size(),',b.size=',b.size(),',c.size=',c.size())
# tensor([[[1, 1],
# [1, 1],
# [1, 1]],
#
# [[2, 2],
# [2, 2],
# [2, 2]]])
# tensor([[[2, 1, 1],
# [2, 2, 0]],
#
# [[1, 0, 2],
# [2, 1, 0]]])
# tensor([[[4, 3, 1],
# [4, 3, 1],
# [4, 3, 1]],
#
# [[6, 2, 4],
# [6, 2, 4],
# [6, 2, 4]]])
# a.size= torch.Size([2, 3, 2]) ,b.size= torch.Size([2, 2, 3]) ,c.size= torch.Size([2, 3, 3])
# 由此可见:
# a[2, 3, 2]分成两个[3, 2]张量a1,a2;
# b[2, 2, 3]也分成2个[2, 3]b1,b2;
# 然后分别计算a1@b1,a2@b2,得到2个[3, 3]张量c1,c2;
# 最后再将c1,c2拼接成一个张量[2, 3, 3];Embedding总结
|
概述 |
Embedding作用是将一个整数(索引号)转换为一个浮点型向量; |
|
构造参数 |
num_embeddings: int, embedding_dim: int, padding_idx: Optional[int] = None; num_embeddings就是词表的大小vocab_size,也就是词表总长度或者词表元素总数; embedding_dim就是想要转换成的向量的长度;也就是用一个多长的向量来表示一个词; padding_idx表示填充符号的索引位置;否则报错; padding_idx必须小于vocab_size;也就是说padding是vocab中的一个元素; |
|
输入 |
输入参数:input 数据类型:输入张量中的元素必须都是整形,可以为int或者long类型,而不能是浮点型(报错); 数据大小:input中的所有元素都必须小于vocab_size;否则报错; 数据形状:Embedding对输入的size没有要求,可以是任意维度,每个维度可以是任意长度; |
|
输出 |
数据类型:输出是浮点向量的集合,也就是一个浮点张量; 输出形状: 1. 每一个浮点向量的长度都是embedding_size; 2. 输出张量的维度比输入张量维度增加一维; 3. 输出中新增的维度在输入张量的最后面; 4. 如果输入张量维度是N,那么输出张量维度就是N+1; 5. 输入的size是[d1,d2,d3,...,dn],则输出size就是[d1,d2,d3,...,dn,embedding_size]; padding符号: (1) padding_idx输入数据,将被转换为全0.的浮点型向量,长度仍为embedding_size; (2) 输入元素为指定的padding_idx时,就转换为一个全0向量 |
Embedding测试
#Embedding测试
#输入中的任何一个元素的值都应该小于vocab_size也就是位于range(vocab_size)集合内
#如果输入中的元素值>=vocab_size则会报错
# IndexError: index out of range in self
# 输入中的数据类型必须为整形
# emb=nn.Embedding(10,3)
#10超出了最大索引范围0-9,会报错index out of range
# input=torch.LongTensor([[1,2,3,4],[3,4,9,10]])
# print(input)
# res=emb(input)
# print(res)
# 输入中的数据类型必须为整形
#RuntimeError: Expected tensor for argument #1 'indices' to have one of the following scalar types: Long, Int; but got torch.FloatTensor instead (while checking arguments for embedding)
#应当使用Long, Int类型,float等浮点类型不被支持
# input2=torch.Tensor([1,2,3,4])#浮点类型输入不被支持
# res=emb(input2)
# print(res)
# input2=torch.IntTensor([1,2,3,4])#Int或Long类型数据可以作为embed的输入
# res=emb(input2)
# print(input2)
# print(res)
# print(input2.shape)
# print(res.shape)
# tensor([1, 2, 3, 4], dtype=torch.int32)
# tensor([[-1.0568, -0.6534, 0.2371],
# [ 0.1998, -0.1030, 0.4830],
# [-1.7354, 0.3366, -1.0676],
# [ 0.0482, 1.1707, -1.2856]], grad_fn=<EmbeddingBackward0>)
# torch.Size([4])
# torch.Size([4, 3])
#Embedding的作用就是将输入中的每个index整数,转换为一个向量,向量长度就是embedding_size
#输出的数据类型为浮点型,而不是整形
#输出张量比输入多了一维,新维度在原维度后面增加,新维度长度为embedding_size
# input3=torch.randint(0,10,(2,3,4))
# emb=nn.Embedding(10,3,padding_idx=0)
# res=emb(input3)
# print('input size=',input3.size(),',emb size=',res.size())
# input size= torch.Size([2, 3, 4]) ,emb size= torch.Size([2, 3, 4, 3])
#假设输入维度是N,那么输出维度就是N+1,并且是在原维度的最后新增一个维度
# 假设输入的size是[d1,d2,d3,...,dn],则输出size就是[d1,d2,d3,...,dn,embedding_size]
# input3=torch.randint(0,10,(2,3,4))
# emb=nn.Embedding(10,3,padding_idx=15)
#padding_idx表示填充符号所在的索引位置
#padding_idx必须位于range(vocab_size)范围内,否则报错
#AssertionError: Padding_idx must be within num_embeddings
#padding_idx对应的索引号输入数据,将被转换为全0.的浮点型向量,向量长度仍然为embedding_size
#也就是说,系统默认将全0向量作为padding的默认值
# input3=torch.LongTensor([0,5,0,8])
# emb=nn.Embedding(10,3,padding_idx=0)
# res=emb(input3)
# print('input size=',input3.size(),',emb size=',res.size())
# print(input3)
# print(res)
#可见,输入元素为0也就是指定的padding_idx时,就转换为一个全0向量
#第0个元素和第2个元素0就转换为[ 0.0000, 0.0000, 0.0000]
# tensor([0, 5, 0, 8])
# tensor([[ 0.0000, 0.0000, 0.0000],
# [ 1.4194, -1.2603, -0.4194],
# [ 0.0000, 0.0000, 0.0000],
# [ 0.7381, 0.3407, 2.0325]], grad_fn=<EmbeddingBackward0>)size和shape的区别
#size和shape都是用来获取张量的形状的,二者的作用是等价的
#size是一个函数,需要带小括号t.size()
#shape是一个属性,不需要带小括号t.shape
#unsqueeze测试
#unsqueeze函数用来增加维度
#将N维张量扩展为N+1维,一维张量扩展后就变成二维,扩展的维度的size=1
#一维张量size为[5]在第一维扩展后,就变成[5,1],在第零维扩展后,就变成[1,5]
#unsqueeze测试
#unsqueeze函数用来增加维度
#将N维张量扩展为N+1维,一维张量扩展后就变成二维,扩展的维度的size=1
#一维张量size为[5]在第一维扩展后,就变成[5,1],在第零维扩展后,就变成[1,5]
t=torch.arange(1,6)
t1=t.unsqueeze(1)
print(t)
#size和shape都是用来获取张量的形状的,二者的作用是等价的
#size是一个函数,需要带小括号t.size()
#shape是一个属性,不需要带小括号t.shape
print(t.size(),t.shape)
print(t1)
print(t1.size(),t1.shape)
# tensor([1, 2, 3, 4, 5])
# torch.Size([5]) torch.Size([5])
# tensor([[1],
# [2],
# [3],
# [4],
# [5]])
# torch.Size([5, 1]) torch.Size([5, 1])view和transpose的区别测试
#view只是改变形状,而不改变元素的顺序,
# transpose不仅改变形状,同时还会改变元素的顺序
t=torch.arange(1,13)
print(t)
t1=t.view(3,4)
print(t1)
t2=t1.transpose(0,1)
print(t2)
t3=t1.view(4,3)
print(t3)
#view只是改变形状,而不改变元素的顺序,
# transpose不仅改变形状,同时还会改变元素的顺序
# tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
# tensor([[ 1, 2, 3, 4],
# [ 5, 6, 7, 8],
# [ 9, 10, 11, 12]])
# tensor([[ 1, 5, 9],
# [ 2, 6, 10],
# [ 3, 7, 11],
# [ 4, 8, 12]])
# tensor([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])
tt=torch.rand(2,2,3)
print(tt)
tt1=tt.transpose(1,2)
print(tt1)
# tensor([[[0.0230, 0.0851, 0.7434],
# [0.7629, 0.9802, 0.5565]],
#
# [[0.7083, 0.1360, 0.6115],
# [0.6868, 0.4091, 0.1013]]])
# tensor([[[0.0230, 0.7629],
# [0.0851, 0.9802],
# [0.7434, 0.5565]],
#
# [[0.7083, 0.6868],
# [0.1360, 0.4091],
# [0.6115, 0.1013]]])Python内置打包函数zip测试
names=['Tom','Trump','Jorge Bush','Washington']
ages=[33,44,55,66,77,88]
zips=zip(names,ages)
print(zips)
for item in zips:
print(item)
#zip将多个可迭代对象中的对应元素,按照顺序,打包成元组
#如果多个可迭代对象长度不同,则取其中最小的
# <zip object at 0x0000023A89A95108>
# ('Tom', 33)
# ('Trump', 44)
# ('Jorge Bush', 55)
# ('Washington', 66)masked_fill(mask, value)掩码填充测试
需要一个mask矩阵,同时需要一个被填充矩阵,两个矩阵形状相同;
默认按照mask中元素为1的位置,对目标矩阵中的相同位置元素填充为指定值
也可以制定特定条件进行填充;
如果两个矩阵形状不同,则会报错:
RuntimeError: The size of tensor a (4) must match the size of tensor b (5) at non-singleton dimension 1
RuntimeError:张量a(4)的大小必须在非单维1上匹配张量b(5)的大小
mask=torch.tensor([[0,0,0,1],
[0,0,1,1],
[0,1,1,1],
[1,1,1,1]],dtype=torch.int)
t=torch.rand(4,4)
print(t)
#将所有mask元素为0的位置,对应的t的元素填充为0.001
t1=t.masked_fill(mask==0,0.001)
print(t1)
#将所有mask元素为1的位置,对应的t中元素填充为6
t2=t.masked_fill(mask,6)
print(t2)
# tensor([[0.9087, 0.5629, 0.5443, 0.4117],
# [0.9685, 0.2989, 0.4243, 0.3676],
# [0.6670, 0.2702, 0.5861, 0.1568],
# [0.6318, 0.5107, 0.9866, 0.4393]])
# tensor([[0.0010, 0.0010, 0.0010, 0.4117],
# [0.0010, 0.0010, 0.4243, 0.3676],
# [0.0010, 0.2702, 0.5861, 0.1568],
# [0.6318, 0.5107, 0.9866, 0.4393]])
# tensor([[0.9087, 0.5629, 0.5443, 6.0000],
# [0.9685, 0.2989, 6.0000, 6.0000],
# [0.6670, 6.0000, 6.0000, 6.0000],
# [6.0000, 6.0000, 6.0000, 6.0000]])训练流程和GPU的使用
|
套路 |
准备数据集-dataloader-模型-损失函数-optimizer- 训练model.train()-output-loss-optimizer.no_grad()-loss.backward()-optimizer.step()- 测试model.eval()-with torch.no_gard():-outputs-loss-accuracy- 保存-torch.save() 打印-SummaryWriter()
|
|
GPU |
torch.save,torch.load的两种方法(第一种方法的陷阱) ,修改内置模型,使用GPU GPU:网络模型model、数据(input,label),损失函数loss_fn ■使用GPU的第一种方法.cuda() if torch.cuda.isavailabel(): model=model.cuda();#转移到GPU之后,需要再赋值给原变量 loss_fn=loss_fn.cuda();#转移到GPU之后,需要再赋值给原变量 inputs=inputs.cuda();#转移到GPU之后,需要再赋值给原变量 labels=labels.cuda();#转移到GPU之后,需要再赋值给原变量 ■使用GPU的第二种方法.to(device) device=torch.device(‘cpu’)#使用CPU device=torch.device(‘cuda’)#使用GPU device=torch.device(‘cuda:0’)#使用第0块GPU #若果电脑中只有一个GPU,那么cuda和cuda:0,这两种写法等价 device=torch.device(‘cuda:0’if torch.cuda.isavailabel() else ‘cpu’) model.to(device);可以不用再赋值给model inputs=inputs.to(device);需要再赋值给inputs labels=labels.to(device);需要再赋值给inputs loss_fn.to(device);可以不用再赋值给model
计时功能import time start_time=time.time();end_time=time.time() time_elapse=end_time-start_time; |
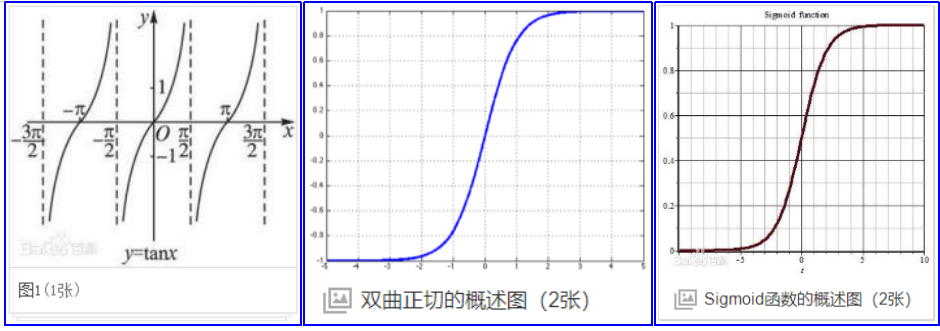
双曲正切函数公式

tan、tanh和sigmoid函数曲线对比
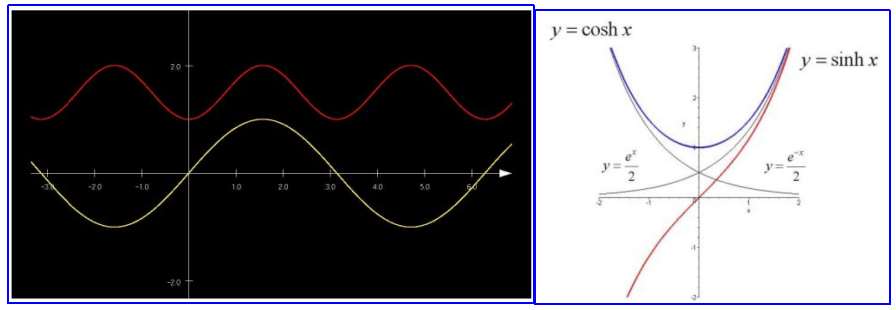
sin和sinh函数图形对比;cos和cosh函数图形对比(形状真的有点像啊,或许这就是函数名称的由来把)
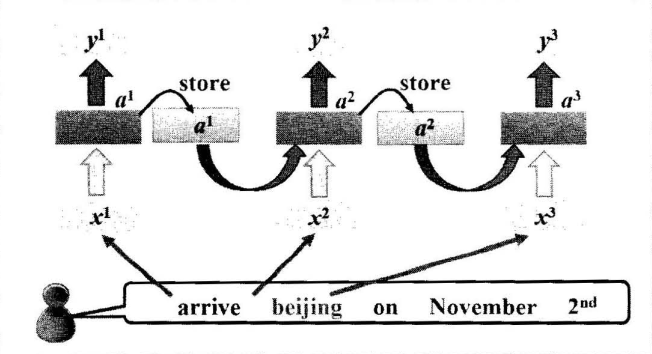
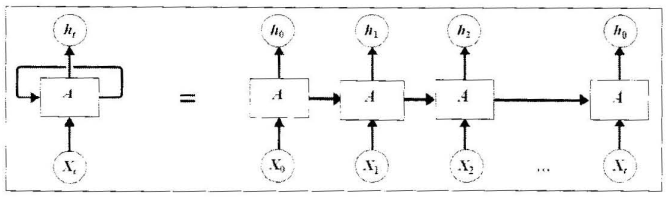
RNN结构图
pytorch保存模型方法
Pytorch 有两种保存模型的方式,都是通过调用pickle序列化方法实现的。
第一种方法只保存模型参数。第二种方法保存完整模型。
推荐使用第一种,第二种方法可能在切换设备和目录的时候出现各种问题。
|
1.保存模型参数方法(推荐):
|
print(model.state_dict().keys()) # 输出模型参数名称 # 保存模型参数到路径"./data/model_parameter.pkl" torch.save(model.state_dict(), "./data/model_parameter.pkl") new_model = Model() # 调用模型Model new_model.load_state_dict(torch.load("./data/model_parameter.pkl")) # 加载模型参数 new_model.forward(input) # 进行使用 |
|
2.保存完整模型(不推荐)
|
torch.save(model, './data/model.pkl') # 保存整个模型 new_model = torch.load('./data/model.pkl') # 加载模型
|
|
3.Transfomers库预训练模型的加载
|
# 使用transformers预训练后进行保存 model.save_pretrained(model_path) tokenizer.save_pretrained(tokenizer_path) # 预训练模型使用 `from_pretrained()` 重新加载 model.from_pretrained(model_path) |
BiGram的中文字符级预测(单向)
测试文档
广州市花都区劳动人事争议仲裁委员会
仲裁裁决书
穗花劳人仲案〔2022〕402号
申请人:何某,男,汉族,1973年2月10日出生,住址:湖南省新田县。
被申请人:广州华宇装饰设计工程有限公司,
地址:广州市花都区建设北路218号沃达商务中心316室。
法定代表人:刘彩凤。
申请人何某诉被申请人广州华宇装饰设计工程有限公司劳动争议一案,本委依法受理并进行开庭审理,申请人何某到庭参加了庭审,被申请人经依法通知后无正当理由未到庭,本委依法对其作缺席审理。本案现已审理终结。
申请人诉称:申请人于2021年4月28日入职被申请人单位工作,工作岗位是泥工,双方没有签订劳动合同,未缴社保,2021年5月15日申请人离职后,双方劳动关系解除。
仲裁请求:1、裁决被申请人向申请人全额支付2021年4月28日至2021年5月15日拖欠的工资,合计人民币11628元。被申请人未予答辩也未提交证据。
本委审理查明:申请人于2021年12月24日向本委申请劳动仲裁。
申请人主张于2021年4月28日入职被申请人单位工作,工作岗位是泥工,双方没有签订劳动合同,没有缴纳社保,由被申请人单位的项目经理郭工招聘过去工作,负责室内的泥水装修,由被申请人负责材料,申请人负责人工,工资按照不同的工序难易程度按不同的单价进行计算,具体工作的地址在广州市花都区建设北路218号沃达商务中心2楼3楼,共产生了人工费11628元。除了申请人外,还有申请人的老婆胡知姻及申请人雇请的一名人员罗利军共同完成该工程,申请人与罗利军约定每天人工费500元共3500元,且申请人已经支付了3500元给罗利军,该工程具体的完工时间是2021年5月15日,完工后申请人当天便离开被申请人公司。
申请人还主张工作的期间被申请人的实际经营者刘建华(法定代表人刘彩凤的丈夫)经常到工地看工程进度,但请假无需经过刘建华的同意,只要将泥水装饰工程按时按质量做好即可。后来,申请人与被申请人于2021年12月4日签订了《付款协议》,但被申请人仍然没有支付过款项给申请人。
申请人为证明其主张,向本委提交了《付款协议》,《付款协议》明确记载了“前有华宇公司尚未支付....泥工费用总额为11628元整,经双方同意于2021年12月20日前付5000元整,剩余的尾款于今年底结清”,该协议盖有被申请人的合同专用章及申请人的签名。
以上事实,有申请人的陈述、有关书证、庭审笔录等为据,证据确实,足以认定。
本委认为:本委通过合法途径将开庭通知书及相关资料送达被申请人,但被申请人没有正当理由拒绝出庭,也没有向本委提交任何答辩资料。根据《中华人民共和国劳动争议调解仲裁法》第三十六条的规定,本委依法对被申请人作出缺席裁决。
申请人主张被申请人还拖欠其工资11628元没有支付,但同时又主张完成工程的除了其本人外还有其老婆及另外雇请的一名工人,同时在完成该工程期间无需接受被申请人实际经营者的管理,而其提交与被申请人签订的《付款协议》中也只是明确为“泥工费用总额”而非工资。本委认为,申请人的主张及证据并不符合劳社部发〔2005〕12号《关于确立劳动关系有关事项的通知》第一条规定的条件,申请人与被申请人之间不存劳动关系。鉴于此,申请人要求被申请人支付其工资11628元,于法无据,本委不予支持。
根据《中华人民共和国劳动争议调解仲裁法》第三十六条、第四十七条、第四十八条、第四十九条,劳社部发〔2005〕12号《关于确立劳动关系有关事项的通知》第一条之规定,裁决如下:
驳回申请人的仲裁请求。
本仲裁裁决为终局裁决,裁决书自作出之日起发生法律效力。如劳动者不服本裁决,可以自收到本裁决书之日起十五日内向有管辖权的人民法院起诉。用人单位有证据证明本裁决有《中华人民共和国劳动争议调解仲裁法》第四十九条第一款规定情形之一的,可以自收到裁决书之日起三十日内向广州市中级人民法院申请撤销裁决。
仲裁员:骆玉仪
二○二二年三月二十四日
书记员:江志炜代码
import json
import math
import os.path
import torch
from torch import nn
from torch.autograd import Variable
from torch.nn import functional as F
CONTEXT_SIZE=2
EMBEDDING_DIM=100
LR=0.001
LOSS=0.01
PATH="doc.txt"
if not os.path.exists("./data"):
os.mkdir("./data")
FOLDER=F'lr{LR}_loss{LOSS}_emdim{EMBEDDING_DIM}'
FOLDER_PATH=f"./data/{FOLDER}"
MODEL_PATH=f"./data/{FOLDER}/model.pkl"
VOCAB_PATH=f"./data/{FOLDER}/vocab.json"
if not os.path.exists(FOLDER_PATH):
os.mkdir(FOLDER_PATH)
file=open(PATH,mode='r',encoding='utf-8')
sen=file.read()
file.close()
trigram=[((sen[i],sen[i+1]),sen[i+2]) for i in range(len(sen)-2)]
vocab=set(sen)#vocab = {set: 356} {'做', '通', '关', '工',
word2index={word:i for i,word in enumerate(vocab)}
index2word={word2index[word]:word for word in word2index}
class NGram(nn.Module):
def __init__(self, vocab_size,context_size,embedding_dim):
super(NGram,self).__init__()
self.n_word=vocab_size
self.embedding=nn.Embedding(vocab_size,embedding_dim)
self.linear1=nn.Linear(context_size*embedding_dim,128)
self.linear2=nn.Linear(128,self.n_word)
def forward(self,x):#x = {Tensor: (2, 356)}
#Embedding层,将字典中汉字的索引号,变成向量
emb=self.embedding(x)#emb = {Tensor: (2, 10)} embedding_dim=10的情况
emb=emb.view(1,-1)#展开emb = {Tensor: (1, 20)} embedding_dim=10的情况
#线性层
out=self.linear1(emb)
#激活函数,加入非线性因素
out=F.relu(out)#out = {Tensor: (1, 128)}
#线性层2
out=self.linear2(out)#out = {Tensor: (1, 356)}
#将矩阵归一化,按照列进行归一化,并取对数
log_prob=F.log_softmax(out,dim=1)
return log_prob
def train(input,epochs,vocab_size,context_size,embedding_dim):
ngram=NGram(vocab_size,context_size,embedding_dim)
optimizer=torch.optim.Adam(ngram.parameters(),lr=LR)
for e in range(epochs):
for index in range(len(input)):
input0=input[index][0][0]#第一个汉字
input1 = input[index][0][1]#第二个汉字
t0= torch.LongTensor([word2index[input0]])#按索引号创建一个张量
t1 = torch.LongTensor([word2index[input1]]) # 按索引号创建一个张量
t=torch.cat([t0,t1],dim=0)#将两个向量按行进行拼接,1行变2行
optimizer.zero_grad()#优化器梯度清零
out=ngram.forward(t)#前向传播 计算出结果 结果是1维向量,长度为字典长度 out = {Tensor: (1, 356)}
real= torch.zeros_like(out)#创建全0向量,长度为字典长度
real_zi=input[index][1] #获取真实值汉字
real[0][word2index[real_zi]]=1 #获取真实值的独热码
loss=F.cross_entropy(out,real)#用交叉熵函数计算损失值 loss = {Tensor: ()} tensor(5.9448, grad_fn=<DivBackward1>)
loss.backward()#反向传播 计算梯度
optimizer.step()#优化参数
print(f'epoch={e} loss={loss.item()}')
if loss<0.01 and e>10:#训练终止条件,损失函数值<0.01并且训练轮数>10
#训练完成时,需要做2件事,保存字典,保存模型参数
file = open(VOCAB_PATH, mode='w', encoding='utf-8')
file.write(','.join(vocab))
file.close()
torch.save(ngram,MODEL_PATH)
break
def predict(input):
#读取本地字典文件
file=open(VOCAB_PATH,mode='r',encoding='utf-8')
vocab=file.read()
vocab=vocab.split(',')
file.close()
word2index = {word: i for i, word in enumerate(vocab)}
index2word = {word2index[word]: word for word in word2index}
input0 = input[0] # 第一个汉字
input1 =input [1] # 第二个汉字
t0 = torch.LongTensor([word2index[input0]]) # 按索引号创建一个张量
t1 = torch.LongTensor([word2index[input1]]) # 按索引号创建一个张量
t = torch.cat([t0, t1], dim=0) # 将两个向量按行进行拼接,1行变2行
#加载模型
ngram=torch.load(MODEL_PATH)#加载模型
out =ngram.forward(t) # 进行预测
out=torch.squeeze(out)#转换为一维
index=torch.argmax(out)#获取最大概率元素的索引
out2=torch.exp(out)
i=index.item()#获取索引值
return index2word[i],math.exp(out[i])#通过索引值获取字符和概率
#train(trigram,100,len(vocab),CONTEXT_SIZE,EMBEDDING_DIM)
input='申请'
pre,prob=predict(input)
print(f'input={input} predict={pre} problity={prob}')
input='法受'
pre,prob=predict(input)
print(f'input={input} predict={pre} problity={prob}')
input='正当'
pre,prob=predict(input)
print(f'input={input} predict={pre} problity={prob}')
input='缺席'
pre,prob=predict(input)
print(f'input={input} predict={pre} problity={prob}')
# 预测结果8.2659e-01
# input=申请 predict=人 problity=0.8265909677808763
# input=法受 predict=理 problity=0.9957110848813666
# input=正当 predict=理 problity=0.9998737733040751
# input=缺席 predict=裁 problity=0.7423789872547777
# word_to_idx={"hello":0,"world":1} #定义词典
# embeds=nn.Embedding(2,5) #2是词典大小,也就是词典元素个数;5是输出向量维度
# hello_idx=torch.LongTensor([word_to_idx['hello']]);
# hello_idx= Variable(hello_idx) #tensor([0]) tensor([0])hello_idx
# hello_embeds=embeds(hello_idx) #tensor([[ 2.3647, 1.1617, -0.8720, -0.0771, 0.7739]], grad_fn=<EmbeddingBackward0>)
# print(hello_embeds)
# idx=Variable(torch.LongTensor([2]))#tensor([2])
# emb=embeds(idx)#IndexError: index out of range in self
# print(emb)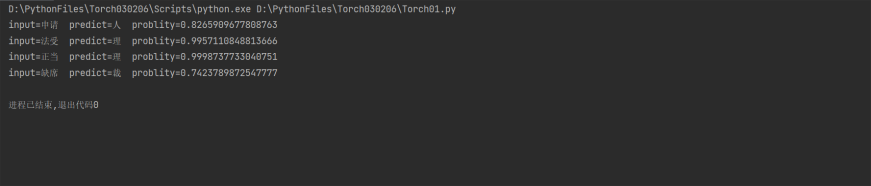
词嵌入测试
import json
import math
import os.path
import torch
from torch import nn
from torch.autograd import Variable
from torch.nn import functional as F
DOC_PATH="doc.txt"
def readFile(path:str):
file = open(path, mode='r', encoding='utf-8')
content = file.read()
file.close()
return content
def writeFile(path:str,content:str):
file = open(path, mode='w', encoding='utf-8')
content = file.write(content)
file.close()
def getCharset(content:str):
chset=set()
for c in content:
chset.add(c)
return chset
#one-hot表示法
def one_hot(s:str,char_set:set()):
char_list=list(char_set)
n_char=len(char_list)+1
tensor=torch.zeros(len(s),1,n_char)
for i,c in enumerate(s):
try:
index=char_list.index(c)
except:
index=n_char-1
tensor[i][0][index]=1 #按照下标对应索引项就是1,其余项全部为0
return tensor
#索引表示法
def str2tensor(s:str,char_set:set):
char_list=list(char_set)
n_char=len(char_list)+1
tensor=torch.zeros(len(s),dtype=torch.long)
for i,c in enumerate(s):
try:
index=char_list.index(c)
except:
index=n_char-1
tensor[i]=index #将字符串中的文字,逐个转换成该文字在词典中的索引号
return tensor
content=readFile(DOC_PATH)
char_set=getCharset(content)
sentence=content.split('\n')[0]
tensor=str2tensor(sentence,char_set)#tensor = {Tensor: (17,)}
print(sentence)
print(tensor)
#输出结果
# 广州市花都区劳动人事争议仲裁委员会
# tensor([120, 36, 236, 167, 34, 222, 72, 171, 153, 135, 87, 112, 57, 342,
# 187, 170, 129])
vocab_size=len(char_set)+1#vocab_size = {int} 357
embed_dim=10
embedding=nn.Embedding(vocab_size,embed_dim)
out=embedding(tensor)
print(out)#out = {Tensor: (17, 10)}
#Embedding层,将一个索引号,或者一组索引号,变成一个指定维度的向量
#每个索引数字,变成一个10维向量,如果是多个索引L批量操作,就变成一个L*10的矩阵
#句子长度对应out的行数,embed_dim对应out的列数
#输入的tensor中的数字,不能超过vocab_size,否则会报错RNN测试
import json
import math
import os.path
import random
import Torch02
import torch
from torch import nn
from torch.autograd import Variable
from torch.nn import functional as F
from tqdm import tqdm #打印训练进度
import matplotlib.pyplot as plt
class RNN(nn.Module):
def __init__(self,word_count,embedding_size,hidden_size,output_size):
super(RNN, self).__init__()#调用父类构造函数
# 用于隐藏层输出的初始化;因为第一个状态时,还没有隐藏层输出,因此需要提供一个初始值
self.hidden_size=hidden_size
self.embedding=nn.Embedding(word_count,embedding_size)#词嵌入层
self.i2h=nn.Linear(embedding_size+hidden_size,hidden_size)#输入到隐藏
self.i2o=nn.Linear(embedding_size+hidden_size,output_size)#输入到输出
self.softmax=nn.LogSoftmax(dim=1)
# input_tensor = {Tensor: (1,)} tensor([2621]) hidden = {Tensor: (1, 128)}
def forward(self,input_tensor,hidden):
word_vector=self.embedding(input_tensor)#word_vector = {Tensor: (1, 200)}
combined=torch.cat((word_vector,hidden),dim=1)#combined = {Tensor: (1, 328)}
hidden=self.i2h(combined)#hidden = {Tensor: (1, 128)}
output=self.i2o(combined)#output = {Tensor: (1, 2)} tensor([[-0.7358, 0.3330]]
output=self.softmax(output)#output = {Tensor: (1, 2)} tensor([[-1.3640, -0.2952]]
return output,hidden
def init_hidden(self):
return torch.zeros(1,self.hidden_size)
# content=Torch02.readFile(Torch02.DOC_PATH)
# char_set=Torch02.getCharset(content)
#
# vocab_size=len(char_set)#词表的长度,决定了onehot向量长度,用于创建Embeddings层
# embedding_size=200#将一个字符,用多少维的向量表示;这里是用一个200维的向量表示一个中文字符
# hidden_size=128#隐藏层的输出维度;隐藏层的输出将和下一个字符合并,共同作为下一个状态的输入
# n_catagory=2 #分类个数,也就是输出维度;几分类问题,输出维度就是几维;二分类问题,输出维度就是2维
# rnn=RNN(vocab_size,embedding_size,hidden_size,n_catagory)
# sentences=content.split('\n')#将文章按照换行符进行切分
#将第一句转换为索引序号的向量,向量长度就是该句话的字符个数,向量的元素值就是该句话中各个中文字符在词表中的索引号
# input_tensor=Torch02.str2tensor(sentences[0][0],char_set)
# hidden=rnn.init_hidden()
# print('iniHidden=',hidden.size())
# output,hidden=rnn(input_tensor,hidden)
# print('input_tensor=',input_tensor.size())
# print('output=',output.size())
# print('hidden=',hidden.size())
# iniHidden= torch.Size([1, 128])
# input_tensor= torch.Size([1])
# output= torch.Size([1, 2])
# hidden= torch.Size([1, 128])
#input_tensor = {Tensor: (22,)} tensor([2621, 1254, 2295, 1749, 400, 1742, 1565, 702, 379, 2849, 121, 3051, 2671, 880, 343, 2904, 2670, 2631, 28, 2762, 661, 2949])
def run_rnn(rnn,input_tensor):
hidden=rnn.init_hidden()
for i in range(input_tensor.size()[0]):
input_char_tensor=input_tensor[i].unsqueeze(dim=0)#input_char_tensor = {Tensor: (1,)} tensor([2621])
#input_char_tensor2=input_tensor[i]#input_char_tensor2 = {Tensor: ()} tensor(2621)
output,hidden=rnn(input_char_tensor,hidden)
return output
# s=sentences[0]#'广州市花都区劳动人事争议仲裁委员会'
# #input_tensor = {Tensor: (17,)} tensor([341, 14, 15, 143, 179, 16, 350, 295, 310, 114, 6, 303, 156, 146,107, 298, 253])
# input_tensor=Torch02.str2tensor(s,char_set)
# output=run_rnn(rnn,input_tensor)#output = {Tensor: (1, 2)} tensor([[-0.2210, -1.6179]], grad_fn=<LogSoftmaxBackward0>)
# print(output.size())#torch.Size([1, 2])
learning_rate=0.005
#模型训练
#input_tensor = {Tensor: (22,)} tensor([2621, 1254, 2295, 1749, 400, 1742, 1565, 702, 379, 2849, 121, 3051, 2671, 880, 343, 2904, 2670, 2631, 28, 2762, 661, 2949])
def train(rnn:nn.Module,criterion:nn.NLLLoss,input_tensor:torch.Tensor,category_tensor:torch.Tensor):
rnn.zero_grad()
output=run_rnn(rnn,input_tensor)#output = {Tensor: (1, 2)} tensor([[-0.9067, -0.5173]], grad_fn=<LogSoftmaxBackward0>)
loss:torch.Tensor=criterion(output,category_tensor)#category_tensor = {Tensor: (1,)} tensor([1])
loss.backward()
#p = {Parameter: (128, 328)} Parameter containing:\ntensor([[-0.0452, -0.0415, -0.0356,
parameters=rnn.parameters()
for p in parameters:
p.data.add_(p.grad.data,alpha=-learning_rate)
return output,loss.item()
#模型评估
def evaluate(rnn,input_tensor):
with torch.no_grad():
hidden=rnn.init_hidden()
output=run_rnn(rnn,input_tensor)
return output
path0='sina_title/junshi.txt' #label=0
path1='sina_title/yule.txt' #label=1
vocab_path='vocab.json'
def get_data():
junshi=Torch02.readFile(path0)
yule=Torch02.readFile(path1)
vocab=set(junshi+yule)
vocab_str=json.dumps(list(vocab),ensure_ascii=False)
Torch02.writeFile(vocab_path,vocab_str)
junshi_list=junshi.split('\n')
yule_list=yule.split('\n')
junshi_dic=[(item,0) for item in junshi_list]
yule_dic=[(item,1) for item in yule_list]
combined_dic=junshi_dic+yule_dic
random.shuffle(combined_dic)
train_data=[]
test_data=[]
for item in combined_dic:
if random.random()>0.2:
train_data.append(item)
else:test_data.append(item)
train_str=json.dumps(train_data,ensure_ascii=False)
Torch02.writeFile('train_data.json',train_str)
print(f'write succeed train_data.json item count={len(test_data)}')
test_str=json.dumps(test_data,ensure_ascii=False)
Torch02.writeFile('test_data.json', test_str)
print(f'write succeed test_data.json item count={len(test_data)}')
train_path='train_data.json'
test_path='test_data.json'
def load_data():
train_str=Torch02.readFile(train_path)
train_data=json.loads(train_str)
test_str=Torch02.readFile(test_path)
test_data=json.loads(test_str)
vocab_str = Torch02.readFile(vocab_path)
vocab=json.loads(vocab_str)
return train_data,test_data,vocab
#get_data()
#print('succeed')
# def label2tensor(label:int,catagory:int):
# res=torch.zeros(1,catagory,dtype=torch.long)
# res[0][label]=1
# res=torch.log(res)
# return res
def write2json(path:str,list_obj):
s=json.dumps(list_obj,ensure_ascii=False)
file=open(path,mode='w',encoding='utf-8')
file.write(s)
file.close()
def read_json(path:str):
file = open(path, mode='r', encoding='utf-8')
s=file.read()
obj=json.loads(s)
return obj
epoch=3 #训练轮数
criterion=nn.NLLLoss()#损失函数
train_data,test_data,vocab=load_data()#加载数据
word_count=len(vocab)+1 #
embedding_size=200#用200维的向量表示一个汉字字符
hidden_size=128 #隐藏层维度
n_catagory=2#二分类问题(军事or娱乐)
rnn = RNN(word_count, embedding_size, hidden_size, n_catagory)#构建模型
rnn_path='rnn_parameter.pkl'#模型参数保存路径
loss_path=f'loss_data_lr{learning_rate}_epoch{epoch}.json'#loss数据保存路径,用于可视化
def start_train():
loss_sum = 0
all_losses = []
plot_every = 100
for e in range(epoch):
print(f'epoch={e+1}')
for index,(title,label) in enumerate(train_data):
title_tensor=Torch02.str2tensor(title,vocab)
label_tensor=torch.tensor([label],dtype=torch.long)
output,loss=train(rnn,criterion,title_tensor,label_tensor)
#output = {Tensor: (1, 2)} tensor([[-0.6152, -0.7777]], grad_fn=<LogSoftmaxBackward0>)
# output2=torch.exp(output)#output2 = {Tensor: (1, 2)} tensor([[0.2457, 0.7543]], grad_fn=<ExpBackward0>)
# output3=torch.log(output2)#tensor([[-0.6152, -0.7777]], grad_fn=<LogSoftmaxBackward0>)
loss_sum+=loss
if index%plot_every==0 and index!=0:
cur_loss=loss_sum/plot_every
all_losses.append(cur_loss)
loss_sum=0
print(f'index={index} progress={int(float(index)/len(train_data)*1000)/10.0}% loss={cur_loss}')
torch.save(rnn.state_dict(),rnn_path)
print('model saved success,path='+rnn_path)
write2json(loss_path,all_losses)#从第一个数据开始,第0个数据舍弃(训练前的数据,无意义)
def plot(data):
plt.figure(figsize=(10,7))
plt.ylabel('Average Loss')
plt.plot(data)
plt.show()
def start_evaluate():
rnn.load_state_dict(torch.load(rnn_path))
print('model load success,path='+rnn_path)
c = 0
for title, label in tqdm(test_data):
title_tensor = Torch02.str2tensor(title, vocab)
label_tensor=torch.tensor([label],dtype=torch.long)
output = evaluate(rnn, title_tensor)
topn, topi = output.topk(1)
if topi.item() == label_tensor[0].item():
c += 1
print('predict accuracy=', c / len(test_data))
do_train=False
if do_train:
start_train()
loss_data=read_json(loss_path)
plot(loss_data)
else:start_evaluate()
#lr=0.005 epoch=1 predict accuracy= 0.514792899408284 bad
#lr=0.001 epoch=3 predict accuracy= 0.8994082840236687 good good
#lr=0.001 epoch=5 predict accuracy= 0.8944773175542406 good
#lr=0.005 epoch=3 predict accuracy= 0.514792899408284 bad数据集为新浪滚动新闻的标题 junshi.txt yule.txt 每个分类包含大约2500个标题
lr设置为0.001 训练3轮时,效果最好,预测准确率达到89.9%
loss曲线如下所示
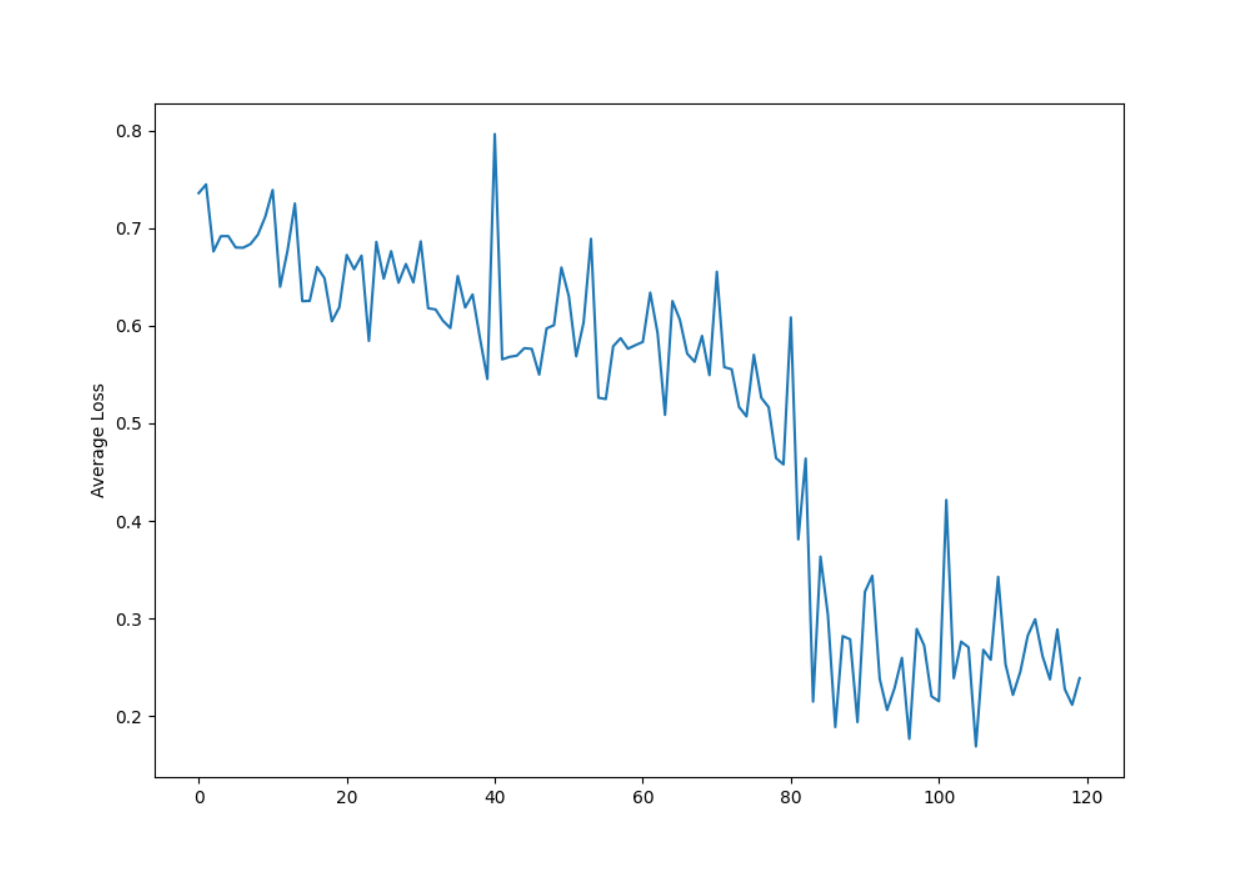
#end



 浙公网安备 33010602011771号
浙公网安备 33010602011771号