关于某些贪心的证明
用排序的贪心一般用微扰法（邻项交换）。
每次决策都是类似的结构的贪心，可以用归纳法证明。
check(x)表示能否将数列分成不超过\(M\)段，每段和的最大值不超过\(x\)。
首先\(ans\)肯定是满足这个判定的，而且小于\(ans\)的分法，分成\(M\)段都不行，分成更少段只会让和的最大值更大，肯定也是不满足判定的。
\(t>ans\)，\(ans\)满足判定的方案，也是\(t\)满足判定的方案，因为\(sum_{max}\le ans < t,sum_{max}\le t\)。
有不超过\(M\)段的不超过，就是为了构造单调性。
check使用了贪心，每次决策都是选择连续地一段，考虑归纳法证明。
假设已经分了\(k\)段，并且这样分能够包含最优解（决策包容性），现在分第\(k+1\)段。
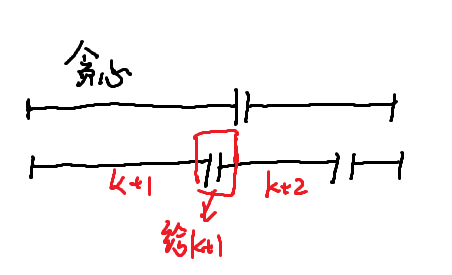
进行如上调整后，可以将任意解变成\(k+1\)段贪心选择的方案（\(k+1\)段和不超过，\(k+2\)段和变小，肯定也不超过\(x\)），而且段数没有变多，所以贪心解就是最优解。
可以反证来理解：假设此段非贪心选法取得最优解，而贪心选法不能取得最优解，通过调整会发现非贪心选法取得的最优解，也可以被贪心选法取到，于是矛盾。
假设答案是每排\(d\)个人，会发现\(d+1\)一定不行，\(d-1\)一定可以（去掉末尾的一个人就是合法方案），于是问题有单调性。
关键是这个check：从一堆人里面选\(k\)组人数一样的人出来，身高绝对值不超过1，能不能选出来。
直觉地想，要让尽可能多的人被选，那就尽量选地紧凑一些。
也就是第一排从\(c_1\)选，第二排从\(c_1\)选，...，直到不够了，第五排从\(c_1,c_2\)选，……。
假设前\(k\)排的贪心选法都是包含最优局面的，现在选\(k+1\)排。
从白色的格子选。
如果当前的\(c_i\)和\(c_{i+1}\)在最优解中没选\(x\)。
- 加起来不够，不可能有一排包含了\(i,i+1\)，因为他们全部加起来也不够，贪心选法是唯一的选法，因为此时一定不选。
- 加起来够，多了一排，反而更优。
否则，这两个身高在最优解中有选。
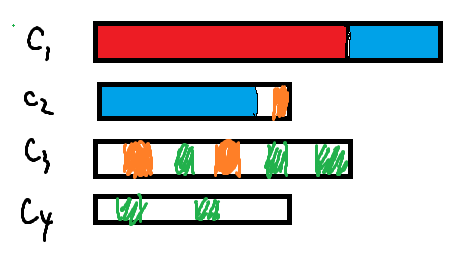
将这两排（橙色）的挪到前面，与后面配对的（绿色）挪到后面，会发现也是合法方案。因为每一个身高的人之间没有区别，\(c_3\)中橙色和绿色的完全可以交换，然后使得橙色都在绿色左边或者上边，然后再将橙色平移，就变成了贪心解，而且排数没有变少。
其实就是如果\(c_{i+1}\)不和\(c_i\)配成一排，而是自己或者和\(c_{i+1}\)配成一排。
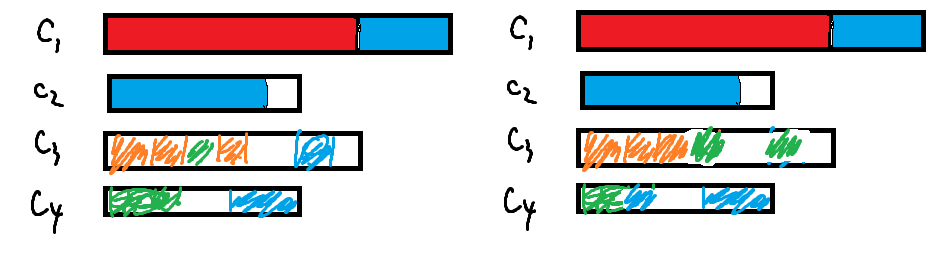
其实就是任何两个方案如果有交叉，都可以交换使得他们依次排开，然后这样把橙色平移，就构造出了贪心解。
没想出来是因为人不一定要连续，甚至方案可以交叉，但是想到可以交换人，使得方案依次排列之后，肯定就像题解说的一样，左端点尽可能靠前，肯定不劣。
浙公网安备 33010602011771号