Taxi
Update on 2023.10.22
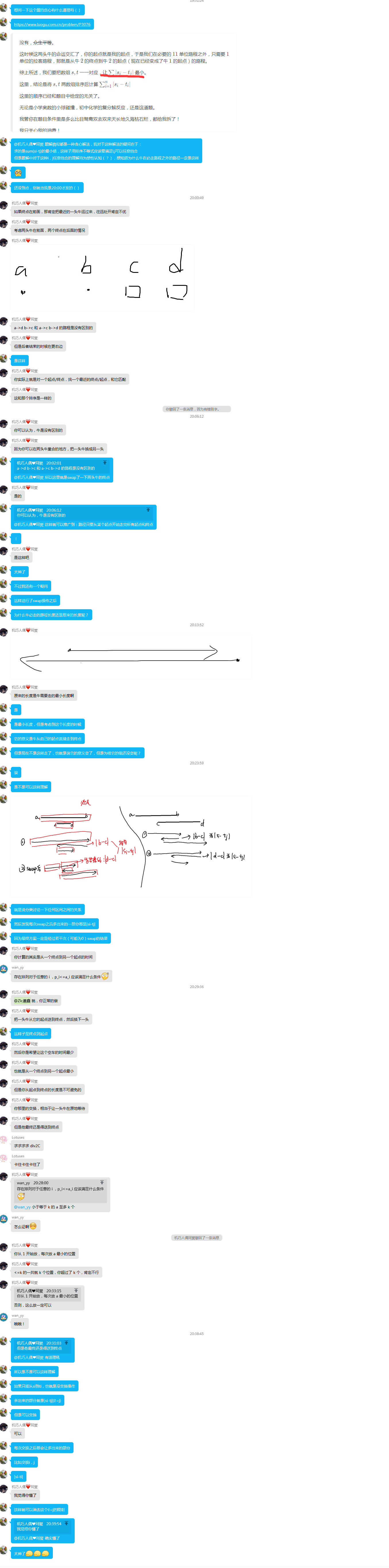
其实就是swap一次,两次,……
swap任意多次之后,就会让s和t自由组合。
然后发现原来必须走的路,其实还是必须走的。
只是换了牛之后多出来的路程会变成自己的起点到自己的终点。
其实,在你swap的时候,两个牛的终点可能已经swap过了。
s[i],t[i]为该牛swap到现在的值。
swap(a,b)(从st来,走到ed),相当于|st-s[a]|+|t[a]-s[b]|+|t[b]-ed|->|t[b]-s[b]|+|st-s[a]|+|t[a]-ed|,(如果先到b的起点也一样的结论)。
st s[a]
t[a] s[b]
t[b] ed
st s[a]
t[b] s[b]
t[a] ed
不难发现,如果把对应的si和tj(多出来的路程)写成两列,其实swap就是swap了t[a]和t[b],因为可以一直swap,相当于t的全排列都可以swap。
注意,起点0和终点n的位置是固定的,不能swap,但是因为他们一个最小,一个最大,排序之后天然满足了不会变位置的性质。
就ok了。
这道题很恶心,终于想通了……
首先是考场做法,先模拟一下样例,猜结论。
首先直觉上告诉我们:一定要尽量让牛在车上,不要空车,也就是只有到了有牛的地方或者终点才会让牛进行上车、下车的操作。
然后就是车肯定至少要开牛的路程之和,然后让多出来的那部分最小。
根据这个样例模拟一下最优解和非最优解,发现多出来的那部分都是 0到某个起点,某个终点到某个起点,某个终点到m。
这时候根据我们的经验,将0和m分别视为一个终点和起点,然后多出来的部分就是终点到起点任意组合(猜的)的距离之和的最小值。
这样子的距离之和最小,用一下排序不等式的变形,就搞定了。
如果是考场,多模拟几个数据,就不难发现大概率是正确的,大不了写个搜索对拍验证一下。
上述做法十分不严谨,并且题解乌烟瘴气,都是这种解释。
- 为什么不空车,答案是最优的?
从0号点出发,经过若干个点,最后到m号点。
不妨把中间走过的点记成A。
那么路径就是0->A[1]->A[2]->...->A[size]->m。
定义数组x:从1到n看每个A[i],如果在走到A[i]时,至少进行了下面操作中的一种,就将A[i]加到x的末尾。
- 有牛下车;
- 有牛上车;
每条路径与数组A一一对应,两者等价,将数组A按照其构造出的数组x分类,考虑分别求每一类子集的最优解。
路径就是0...x[1]...x[2]...x[3]...x[k]...m。(...表示经过若干点(可以不经过点))
根据题意,合法的路径是:
对于每头牛i,如果在
x[j]上的操作有操作牛i,则称i和x[j]相关。对于每头牛i,将它相关的x[i]拿出来,就是x[p1], x[p2], ..., x[p(k-1)], x[pk]。由题意,一开始牛都在路上,所以x[p1]必然是让i上车;x[p2]必然是让i下车,……而且第一次上车一定在s[i],最后一次下车一定在t[i],所以x[p1]==s[i], x[pk]==t[i]。
反之,如果x数组里面,每头牛相关的x[j]都满足上车、下车成对出现,并且
x[p1]==s[i], x[pk]==t[i],那么按照这样走,能够满足题意。
由两点间距离最短(路程一定不小于位移,看做公理),记d(a, b)为a到b的路程,s(a,b)为a到b的位移。
则d(0,x[1])+d(x[1],x[2])+... >= s[0, x1] + ... = |0 - x1| + |x1 - x2| + |x2 - x3| + ... = t。
所以这个子类里面的最优解一定大于等于t,而且t对应的方案就是从0直走到x1,……,从xk直走到m,由于x数组没变,所以路径是合法路径,所以最小值此时是t。
由于上车下车一定成对出现,如果有x[i]有上、下车操作,并且不在s数组中(除了最后一次到终点),那么这个方案要么不是最优解、要么有别的上车的x都在s里的方案是最优解。
一头牛niu相关的x:
s[niu], x[p1], x[p2], ..., t[niu],我们将每两个相邻的元素称为成对,比如x[p1]和x[p2]就成对,x[p3]和x[p4]也成对。
由于下车之后牛只能待在原地,所以下次该牛只能从同一个地方上车,成对的x是相等的,比如
x[p1]==x[p2]。
任意取一个不在s里面坐标o,它对应的x对x[i],x[j]。那么路径是这样:

niu相关的x:s[niu], ..., x[i], x[j], x[k1], x[k2], ..., t[niu]。
把x[i]和x[j]上关于牛的操作删去,niu的相关x还是合法的,其他牛不变,整个x还是合法的。
对于每头牛,都进行上述操作,最后得到了一个新得到合法的x序列。
此时的所有上、下车操作,都一定是在s里面进行的(除了最后一次,最后牛下车就不会再上车了),如果原来有一个x[k]不在s里,那么它此时已经没有操作了,根据x的定义,它已经被删去了。
也就是此时的x删去了一些数。
需要知道的一个基本事实是:路径中每删去一个数,绝对值之和(距离之和)肯定不会变差。
因为|a - b| + |b - c|相当于是a到c的路程,|a - c|相当于是a到c的位移,前者肯定不比后者小。
归纳法:每删一个数都不会变差,全部删完肯定不会变差。
至此,已经证明了有让牛换乘的操作时,一定是在有别的牛的地方进行的。
也就是说尽量不空车的直觉是正确的。
- 如何统计答案?
由于车上只能载一头牛,所以至少要走这么多路。
如果走的比这个还少,就算一直在某条si到ti的位移上,也没法走到所有的ti,就不合法了。
接下来看多出来的那部分,设为k。
首先,加入没有换乘操作,路径就是0->s1->t1->s2->t2->s5->t5->...->m,不难发现,k就是从0到任意一个起点a,从a对应的终点到任意一个起点b,……,从f对应的终点到m。
需要注意,这里还不能直接用排序不等式,因为牛x的终点到的起点不能是自己的起点,有了这个限制就不能直接排序了。
把路径里面的si和ti保留第一个和最后一个,也就是保留牛相关的x中的第一个和最后一个数。
这样的路径一定不是严格最优解...s[x]...s[y]...t[x]...t[y]...。
因为到t[x]时x一定要下车,s[y]又让y上车了(x下车),所以又要回到s[y]让x上车;最后要在t[y]让y下车,又要回到s[y]接y。
对于y而言,相关的x:s[y](1), s[y](2), s[y](3), ... , t[y]。
在整个路径中s[x]...s[y](1)...s[y](2)...t[x]...s[y][3]...t[y]
删掉前两个s[y]还是合法的x,所以还是合法路径,并且删点不会让路径边长,证毕。
貌似没用
因为牛没区别,换乘可以看作交换两个牛的终点……
貌似只能大概模拟一下样例,感觉就是可以用排序不等式任意组合,但是证不出来……
于是上述排序不等式用不了的限制就没有了,完事了。
呼~~~~
不管了,就这样吧……




 浙公网安备 33010602011771号
浙公网安备 33010602011771号