贪心

这玩意真的很烦，贪心题不分难度我都想不出来……

也许是写的题太少了……

---

2023.9.27

P1367 蚂蚁

先不要管蚂蚁的编号，也就是把所有蚂蚁看成无差别的。

贪心里面貌似非常喜欢无差别这个性质：因为无差别，所以A，B相遇之后掉头，其实相当于继续往前走（而且方向不变），因为蚂蚁们没有区别。

然后就可以直接算出所有蚂蚁最终的位置。

可是题目要按照编号输出，怎么办呢？

我们发现对于一个蚂蚁A，如果它初始时左边的蚂蚁是L，右边的蚂蚁是R，那么它最终一定是在L和R中间，因为它一碰到L（或者R），就会往回弹，它永远不可能穿过去。

对于任何一只蚂蚁，它们的相对位置肯定就是初始时的相对位置。

证明：假设不是初始的相对位置，那么一定有一对蚂蚁x和y，x一开始在y左边，然后在y右边，那么x必然要穿过y，而这是不允许的。

所以再记一下从左到右每个蚂蚁应当是编号是多少的蚂蚁，记到编号数组里面，按照顺序输出就行了。

[USACO13FEB] Taxi G

我们惊奇地发现，这道题里面的牛没有区别，这就想到了贪心。

我们注意到，Bessie可以在任意位置把奶牛踢下车，这就造成了过多情况，不方便分析。

首先，如果车上没有奶牛，路上也没有奶牛，那么直接跨过这段路不作停留一定最优：不然的话，减去重复走的路，直接跨过去，路程肯定更小。

---

那么车上如果有奶牛呢？

直觉告诉我们，如果有一段路上没有任何其它奶牛等待上车，那么直接载着一只奶牛走完这段路程，肯定比在路上放下奶牛更优。

下面来证明这个结论。

在任意时刻，任意地点，假如有一段没有待上车的奶牛的路（黑色的）。

Bessie可以向左走，也可以向右走，不妨先看向右走的情况。

假如当前奶牛i的终点在当前位置p的右边。

对于任意一种走法中，红色路段的路程是sum。

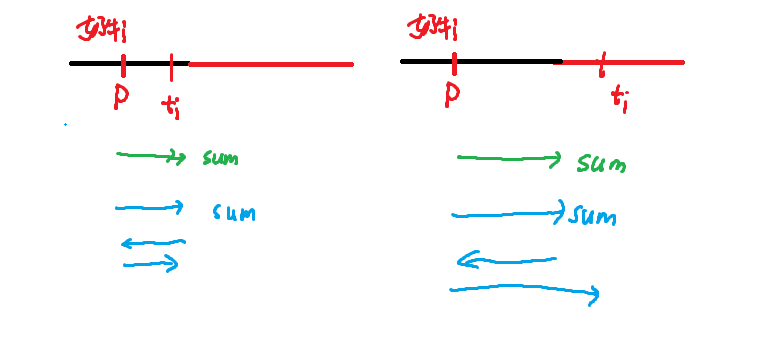
容易发现，绿色路径（不放下奶牛）的长度一定更小。

---

因为两头牛没有区别，所以踢出牛x的操作其实看成牛x还是继续坐车上，只是终点变成牛y的终点，牛y的终点变成牛x的终点（交换一下终点）。

因为可以随便踢出牛，所以其实牛的终点可以和起点随便搭配。

这样子问题转换成了没有换牛操作的问题了。

那么，载着一头牛到处转，你又不能换掉它，最小路径肯定就是直接到终点了，然后可以选择下一个牛，去接它，同样直线最短。

假设t1[i]表示搭配之后的终点，那么路径就变成了。

0->s[1]->t1[1]->s[3]->t1[3]->...->s[2]->t1[2]->m

里面1，2，3……的顺序可以随意，因为路径可以任意走。

那么便是从起点到终点，和从终点到下一个起点的路径和，后者用一下排序不等式就可以求得最小值。

前者能否也用排序不等式呢？

终点到的下一个起点，不能是自己的起点。

---

首先我们考虑，如果不能路上换牛，应该怎么做。

那么载上一头牛之后，必然直接到它的终点，路径最短，不然只能多走路，而且最后一定要到终点才能载其它牛。

那么路径长度就是
0->s[1]->t[1]->s[2]->t[2]->s[3]->t[3]->...->m

把0看成一个终点，m看成一个起点。

也就是所有|s[i]-t[i]|加上n+1组终点到下一个起点的距离最短。

将任意一种走法，按照顺序列出来

0->...
t[1]->...
t[2]->...
t[3]->...
...
...->m