欧拉路径和欧拉回路

这是之前关于欧拉路的两篇博客。

关于欧拉路的逆序压栈问题：here。

22年写的一个小总结：here。

关于欧拉路，主要疑点在于两个：一是压栈输出的原理；二是打上标记后时间复杂度退化的问题。

压栈输出的原理

走到点u时，有两种情况：

1. u此时是终点，那么没有没走过的边与之相连。
2. u此时不是终点，那么它一定还要继续走，也就是还有没走过的边与之相连。

注意：u此时不是终点，不代表它一定不是终点，因为一个点可能重复经过，就好比下面那个图，1号点一开始不是终点，但是最后可能是终点。

所以，终点就是走不动的点，那么对于一条合法的欧拉路，终点肯定是在最后输出的。

然而，我们在搜索的时候，并不知道哪个点是终点，这该怎么办呢？

此时用到上面的性质，我们知道如果一个点是终点，那么它就不能继续走下去；而如果一个点不是终点，它一定会走下去（因为存在欧拉路，而且边没走完）。

对应到搜索中，就是终点会最早回溯，最早入栈，自然也就保证了它最后输出。

直接输出的话，可能会先访问到终点，然后先输出终点，这是错误的。

这里就有一个问题：除了终点之外的其他点的枚举顺序，会不会导致无法枚举到正确的欧拉路径呢？

其实不是不会的，考虑一个有向图中的点u，这个点连到了一些入边和出边（还没走过），由于它必然走完所有边，而且每条出边只能从u开始走，所以每走完一条出边之后必然通过一些方法回到u。

也就是... u ... u ... u ... u ...

由于整个路径上的边都是不重复的，对于每一个从u出发，再回到u的路径，两两之间肯定是没有重复路径的。

所以它们其实是独立的，先走哪条边都不会影响别的边。

这也就提供一种求字典序最小的方法：

1. 终点的位置是确定的，此时从小到大枚举出点，如果它是终点，那么它一定在最后，如果它不是终点，先访问的点后入栈，先输出，保证了字典序最小。
2. 终点的位置不确定，任何点都可以是终点，先访问的点后入栈，先输出，同样字典序最小。

打上标记后时间复杂度为何会退化

考虑这样这个图（无向图，有向图的情况，图中的无向边{u, v}改成两条有向边(u,v), (v,u)即可。）：

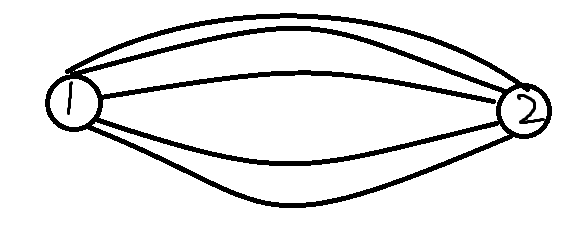
n=2，只有两个点，共有m条边，现在来看下打标记的做法会遍历多少次边。

记u：cnt，为第cnt次经过u号点。

1:1，此时遍历到h[u]就会递归到2。
2:1，此时遍历到h[u]就会递归到1。
1:1，此时会遍历e[1]，发现边有标记，然后到e[2]，递归到2。
2:2，此时会遍历e[1]，发现边有标记，然后到e[2]，递归到1。
……

观察一下，1：1后，经过了1条边，2：1后，经过了2条边，1:2后经过了3条边，2:2后经过了4条边，1:3经过了5条边……

不难发现，2：x后经过了2x条边，那么也就是说，对于二号点，直到走完了m条边递归才会结束，也就是递归了m/2次。
1号点的递归次数也大致是m/2次。（之所以是大致，是因为根据不同实现方式，可能会多一两个常数）。

对于1号点：1:1，遍历1个出边；1:2遍历2个出边；……1：m/2，遍历m/2个出边，一共遍历了m^2级别的边。

二号点也是如此，所以会超时。

所以此时，我们考虑实时更新h[u]，让后面重复递归的点不再枚举到走过的边，将边真正意义上删除。

然而，此时还没考虑递归结束后回溯的情况。

1:1，回溯之后还会遍历2、3、……m的出边。
1:2，回溯之后还会遍历3、……的出边。

总共也是m^2级别的打过标记的边数。

也就是说，后递归的点总过的边，应当不让之前递归的点再走，可是我们明明已经删去了这条边啊，为什么这样呢？

其实这样的：

我们递归删边的时候，将h[u]连到了后续节点，但是不论怎么连，当前点枚举时候使用的局部变量i都不会被更新。

所以，其实我们的i应当改为h[u]，这样才能保证后续删去的边不会在回溯时被遍历到。

记录路径时，记录点和记录边的区别

记录点时，压栈写在最后；记录边时，压栈写在循环中。这两者有什么区别和联系呢？

其实，找欧拉路可以看成这样：

这是欧拉路径：

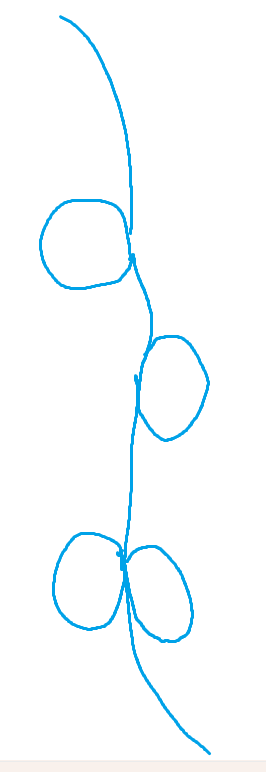
这是欧拉回路：

图中的线表示路径，圆圈表示走过的还，可以发现，欧拉路径相比回路，就是多了一个不能回到出发的点路：通向终点的路。

这在逆序压栈里面讲得很清楚了。

其实记边路径也可以在循环外面记，只是这样dfs函数要多一个参数：来的时候走的边，相当于把边放在它的后继上统计，但是这样不优美，因为起始点不是后继，要特判；而放在循环里面记，相当于把边放在它的前驱统计，而前驱是一定会循环的，不是前驱的点，不会循环，不用特判，十分优雅。

记点的路径的时候也是一样，可以写在循环里面，但是起始点没有前驱，还要特判，一样不优雅。

题单

P1127 词链 需要注意26个字母不一定都存在，在代码中体现为：判断连通块个数时，要将不存在的字母去掉；寻找欧拉路起点时，不能初始化起点为0，因为0（也就是a）可能不存在，然后当每个点出度都等于入度时就会挂掉，应当令start为-1，然后初始化为第一个存在的点或者出度比入度多1的点。

现状

然而，欧拉路好像没什么好考的，因为很难和其他算法结合，灵活性不高，题目也少……