二分图

二分图有关的都放在这里。

---

A：图G是二分图

B：图G中不存在奇数环

C：图G可以进行染色

注：染色法：对于每一条边 \((u, v)\)，u和v应染成不同的颜色（放入两个点集），遍历每一条边看下是否有矛盾即可（具体来说，从1个点出发dfs，如果两个点中有一个未染色，就染成符合条件的颜色，否则检查是否为不同颜色）。

下面证明 \(A \iff B \iff C\)。

• \(B \Rightarrow C\)

假设图G不能进行染色，也就是说染色过程中出现了矛盾。

点u和v都被染色了，说明它们都被遍历过了，也就是在一个连通块中。

又因为之前的染色没有矛盾，所以它们之间存在至少一条合法路径，是黑白黑白...

加上这条矛盾边后，这些合法路径都变成一个环。

也就是我们找到了一条边：

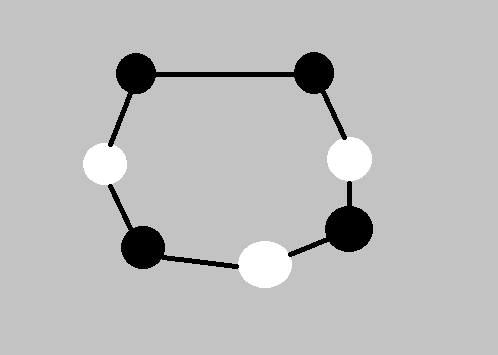
由于起点是黑，终点是黑，所以路径长度必然是奇数，这也就说明了存在一个奇数环，与\(B\)矛盾，假设不成立。

故\(C\)。

• \(B \Leftarrow C\)

假设图G存在奇数环。

将这个环染色，必然出现首尾颜色相同的情况，也就是染色一定失败，与 \(C\) 矛盾，假设不成立，所以 \(B\)。

至此，已经证明了 \(B \iff C\)

PS：这里用反证法是对的，但其实这里的反证法是用了\(\neg q \Rightarrow \neg p\)，则\(p \Rightarrow q\)。

• \(B \iff C \Rightarrow A\)

染色方案中，黑色的点作为一个集合，白色的点作为一个集合，构造出了一种分点的方案，所以G是二分图。

• \(A \Rightarrow B\)

假设二分图G存在奇数环，边两端的点必然在两个集合中，但是因为有奇数环，所以总会一条边上的两个点在同一集合中，也就是在同一集合中，存在了至少一条边，与图G是二分图矛盾，假设不成立，所以 \(B\)。

所以 \(A \iff B\)。

所以 \(A \iff B \iff C\)

PS:其实\(C \Rightarrow B\) 是多余的。

---

最大匹配：选一个边集\(E=\{(u,v)|(u,v)\in E_0\}\)，定义匹配点为\(\{u|u\in E\}\)，定义匹配边为\(\{(u,v)|(u,v)\in E\}\)，非匹配点为匹配点的补集，非匹配边为匹配边的补集。

最大匹配就是要求元素个数最多的一个\(E\)。

增广路径：沿着一个非匹配点出发，走非匹配边、匹配边、非匹配边、……非匹配边（过程中经过的点均为匹配点），最后走到非匹配点。

将边集换为走过的非匹配边，元素个数多一。

事实上，我们有 \(最大匹配 \iff 该匹配中不存在增广路径\)。

下面证明几个结论。

---

• 增广路径一定可以以左边的一个点作为起点。

任何一条起点是右边的点的增广路径，由于走的边数是奇数，所以最后的终点一定是左边的某一个点，由于边是无向边，将终点作为起点即可。

这对应了匈牙利算法中，只枚举左边的点集。

这样子，每条匹配边都是从右边出发到左边，对于了匈牙利算法中的match数组。

同样，每条非匹配边都是从左边出发。

匈牙利算法的find函数，其实就是从一个点u出发，尝试找到一条以非匹配点结尾的增广路径。

• 每一个点，如果有以它为起点的增广路径，只会被枚举一次（然后就变成匹配点，不能作为起点了）。

• 否则，没有以它为起点的增广路径，也就不用枚举它了。

线性枚举1~n，能否枚举到所有增广路径，有点抽象，现在解释不清楚，学完网络流再来填坑。