（严格）次小生成树

Solution I

先求出最小生成树\(T\)。

由于次小生成树\(T'\)一定至少有一条边与\(T\)不同，我们可以枚举每一条边\(e \ in T\)，在删去\(e\)的图上求最小生成树\(T''\)，\(T''\)就是原图上次小生成树\(T'\)。注意虽然只枚举了一条边，但是这只是保证了\(e\)不会被选中，其它边是可以任意选择的，所以这样也能处理有两条边不同，有三条边不同，……这些情况。

CODE:

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 510, M = 10010;
const LL INF = 4e18;

struct Edge
{
    int u, v, w;
    bool min;
    bool operator <(const Edge &t) const
    {
        return this->w < t.w;
    }
}e[M];

int n, m;
LL minv;
int fa[N];
bool tag[M];

int get(int x)
{
    if (fa[x] == x) return x;
    return fa[x] = get(fa[x]);
}

void kruskal(bool flag)
{
    for (int i = 1; i <= n; i ++ )
        fa[i] = i;
    if (flag) sort(e, e + m);
    for (int i = 0; i < m; i ++ )
    {
        if (tag[i]) continue;
        int a = get(e[i].u), b = get(e[i].v);
        int w = e[i].w;
        if (a != b)
        {
            fa[a] = b;
            if (flag) e[i].min = true;
            minv += w;
        }
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i ++ ) 
        scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);

    kruskal(true);
    LL res = INF;
    for (int i = 0; i < m; i ++ )
        if (e[i].min)
        {
            minv = 0;
            tag[i] = true;
            kruskal(false);
            tag[i] = false;
            res = min(res, minv);
        }
    printf("%lld\n", res);
    return 0;
}

但是实现的过程中，我们会发现这种做法不易优化，且不方便求严格次小生成树。

Solution II

首先，我们要证明一个结论：对于任何一棵生成树，如果它存在（严格）次小生成树，那么一定存在一个（严格次小生成树），与自己只有一条边不同。

首先对于次小生成树证明。

假设所有次小生成树都至少有两条边与最小生成树不同，按照边权从小到大检查每一条边，找到第一个两者不同的位置，如下图：

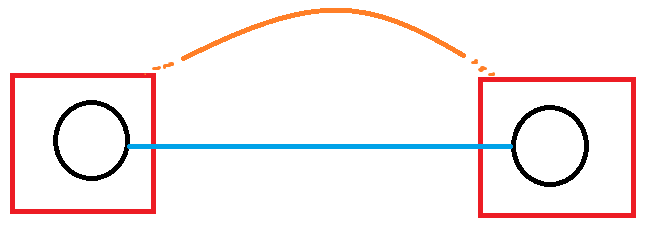
（方框是连通块，黑圈是点A、B，蓝边是最小生成树的边e1，橙边是次小生成树的边e2）

由于A和B一定要连通，所以次小生成树必然选择了e1之后不小于e1的边（边权已经排序），此时将e2从次小生成树中删去，将e1加入次小生成树，会发现得到的树的总权值不大于原来的总权值，并且还与最小生成树不同（至少有两条边不同）。
这样，要么假设中的次小生成树这个前提不成立，要么构造出了一个不同边数少一的次小生成树。重复这个操作直到只有一条边不同，得到的就一定是次小生成树。

证毕。

对于严格次小生成树证明。

同样是上面这个图，也是同样的操作，如e1=e2，直接替换，不同边数-1；
若不同，往后找到另外一条不同的边，将它直接替换，边数也是-1；

证毕。

---

貌似上述这个证法有点问题，就按照算法流程去意会一下吧，先记住做法了。
证明以后再说。

1. 求出最小生成树，标记树边与非树边，同时建立出最小生成树；
2. 求出最小生成树上任意两点间距离的最大值和次大值；
3. 枚举每一条非树边\((u,v,w)\)，如果\(w>max(u,v)\)，直接更新答案\(sum-max(u,v)+w\)；否则与次大值比较，如果比次大值大，直接更新\(sum-lower_max(u,v)+w\)。

PS：所有非树边\((u,v,w)\)，其权值一定大于等于\(max(u,v)\)，因为如果不是，将这条非树边插入，最大边删去，可以得到一棵比最小生成树还小的树，就矛盾了。