EM算法

凸函数

如果一个函数处处二次可微，且对于任意的x都有$f^{''}(x) \ge 0$，则f(x)是凸函数。当x是向量时，$f^{''}(x)$就对应到Hessian矩阵，$f^{''}(x) \ge 0$就对应到Hessian矩阵H是半正定的，即$H \ge 0$。当$f^{''}(x) > 0$或$H > 0$时，f(x)为严格凸函数。

凸函数满足一个性质：对于任意的$\lambda_1,\lambda_2 \in [0,1]$，且$\lambda_1+\lambda_2=1$，有

\begin{equation} \lambda_1f(x_1)+\lambda_2f(x_2) \ge f(\lambda_1x_1+\lambda_2x_2)  \label{convex} \end{equation}

Jensen不等式

把(\ref{convex})式推广一下就得到Jensen不等式。如果f(x)是凸函数，x是随机变量，则有

\begin{equation}E[f(x)] \ge f(E[x]) \label{jensen} \end{equation}

如果f(x)是严格凸函数，则(\ref{jensen})式中等号成立的充要条件是：x是常量。

当f(x)为凹函数时有

\begin{equation} f(E[x]) \ge E[f(x)] \label{jensen2} \end{equation}

带隐含变量的极大似然估计

给定互相独立的训练样本$x_1,x_2,\cdots$，这些样本同时出现的似然函数为

\begin{equation}L(\theta)=\sum_i{logp(x_i;\theta)} \label{lik} \end{equation}

例：有2枚硬币A和B，拿它们做了5次试验，每次试验都是取其中一枚硬币掷10 次，且观察到了每次试验正面向上的次数。求2枚硬币正面向上的概率$\theta_A$和$\theta_B$。

这里面有个隐含变量z：每次试验取的是哪枚硬币。此处z服从伯努力分布。一般情况下z可能服从任意的分布，比如服从正态分布（此时z是连续变量）。

如果知道了隐含变量，那很容易根据MLE（极大似然估计）计算出$\theta_A$和$\theta_B$。如果z是个变量，则似然函数为

\begin{equation}L(\theta)=\sum_i{log\sum_j{p(x_i,z_j;\theta)}} \label{lik_hid} \end{equation}

如果z是连续变量，则上式中的对z求和改为对z求积分。

从(\ref{lik})式到(\ref{lik_hid})式的理论依据为：边际概率等于联合概率对一个变量求积分，即$p(x)=\int_{-\infty}^{\infty}{p(x,z)dz}$。

极大化似然函数需要求似然函数的层数$\frac{\partial L(\theta)}{\partial \theta}$，对(\ref{lik})式求导很容易，因为$log'(x)=\frac{1}{x}$，但是(\ref{lik_hid})式求导就很困难，因为log函数里面又套了一层求和函数。

因此，当含有隐含变量时直接使用极大似然估计遇到了计算困难。除了极大似然估计还有其他方法求解$\theta$吗？有！那就是EM算法！

EM算法

 对于样本$x_i$，设其隐含变量$z$服从分布$Q_i(z)$，$z$为离散变量时$\sum_jQ_i(z_j)=1$，$z$为连续变量时$\int_{-\infty}^{\infty}Q_i(z)dz=1$。下文都以$z$为离散变量为例。

\begin{equation} L(\theta)=\sum_i{logp(x_i;\theta)}=\sum_i{log\sum_j{p(x_i,z_j;\theta)}} \label{em1} \end{equation}

\begin{equation} =\sum_i{log\sum_j{Q_i(z_j)\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}}} \label{em2} \end{equation}

\begin{equation} \ge \sum_i{\sum_j{Q_i(z_j)log\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}}} \label{em3} \end{equation}

(\ref{em1})式到(\ref{em2})式好理解，分子分母同乘以一个$Q_i(z_j)$。(\ref{em2})式到(\ref{em3})式利用了Jensen不等式，把$\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}$对应到(\ref{jensen2})式中的$x$，$log$对应到(\ref{jensen2})式中的$f$，$log$是凹函数。由于$Q_i(z)$是一个概率分布，所以$log\sum_j{Q_i(z_j)\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}}$可对应到$f(E[x])$，$\sum_j{Q_i(z_j)log\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}}$可对应到$E[f(x)]$。

对(\ref{em2})式求最大值是困难的，因为含有和的对数，对(\ref{em3})式求最大值就容易了。

(\ref{em3})式是似然函数$L(\theta)$的下界，根据Jensen不等式，(\ref{em3})式中等号成立的条件是$\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}$为常数，即

$$\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}=c$$

c是常数。因为$\sum_jQ_i(z_j)=1$，所以$\sum_j{p(x_i,z_j;\theta)}=c$。则

$$Q_i(z_j)=\frac{p(x_i,z_j;\theta)}{c}=\frac{p(x_i,z_j;\theta)}{\sum_j{p(x_i,z_j;\theta)}}=\frac{p(x_i,z_j;\theta)}{p(x_i;\theta)}=p(z_j|x_i;\theta)$$

至此我们得到，当固定$\theta$时$Q_i(z_j)$取$p(z_j|x_i;\theta)$（即后验概率），可使得(\ref{em3})式等于$L(\theta)$。这就是E步，固定参数$\theta$，寻找合适的$Q_i(z_j)$，建立$L(\theta)$的下界。接下来是M步，给定$Q_i(z_j)$，调整$\theta$，去极大化$L(\theta)$的下界。可对比下图理解E步和M步：

 

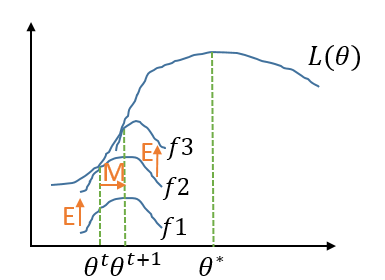
图1 EM算法图示

E步是固定$\theta^t$，找到合适的$Q_i$，把下界从$f1$提升到$f2$，在$\theta^t$处$f2$与$L$相等。M步是固定$Q_i$，从$\theta^t$迁移到$\theta^{t+1}$，求得$f2$的最大值。

EM算法的公式描述如下：

E-step:对于每一个样本$x_i$，利用上一轮迭代得到的$\theta$计算

$$Q_i(z_j)=p(z_j|x_i;\theta)$$

M-step:根据E步到得的$Q_i(z_j)$求$\theta$

$$\theta= \underset{\theta}{arg \; max}\sum_i{\sum_j{Q_i(z_j)log\frac{p(x_i,z_j;\theta)}{Q_i(z_j)}}}$$

循环重复E-Step和M-Step，直到参数收敛。

EM算法的收敛性

 不断重复E-Step和M-Step，$\theta$真的能收敛到$\theta^*$吗？如果我们能证明每轮EM算法得到的$\theta$使似然函数$L(\theta)$都是递增的，即$L(\theta^t) \le L(\theta^{t+1})$，那我们最终得到的$\theta$就是似然函数的极大值点。

\begin{equation} L(\theta^{t}) = \sum_i{\sum_j{Q_i(z_j)log\frac{p(x_i,z_j;\theta^{t})}{Q_i(z_j)}}} \label{convergence1}\end{equation}

\begin{equation} \le  \sum_i{\sum_j{Q_i(z_j)log\frac{p(x_i,z_j;\theta^{t+1})}{Q_i(z_j)}}} \label{convergence2}\end{equation}

\begin{equation} \le L(\theta^{t+1}) \label{convergence3}\end{equation}

结合图1来理解上面的公式，(\ref{convergence1})式是说在固定$\theta^t$的情况下找到了$f2$，使得$f_2(Q,\theta^t)=L(\theta^t)$。(\ref{convergence1})式到(\ref{convergence2})式实际上就是M步，固定$Q$，$f_2(\theta^t) \le f_2(\theta^{t+1})$。(\ref{convergence3})式跟(\ref{em3})式是等价的。正如图1所示，E-Step和M-Step的循环实际上就是坐标上升法，不断逼近函数的极大值。