gauss_jordan法求矩阵的逆
先来点预备知识。矩阵的3种运算我们称之为“行初等变换”:
- 交换任意2行
- 某一行的元素全部乘以一个非0数
- 某一行的元素加上另一行对应元素的N倍,N不为0
以矩阵实施行初等变换等同于在矩阵左边乘以一个矩阵。
当要求矩阵A的逆时,在A的右边放一个单位矩阵,我们称[A|I]为增广矩阵。对增广矩阵实施行初等变换,即左乘一个矩阵P,如果使得P[A|I]=[PA|P]=[I|P],则P就是$A^{-1}$。
通过一系列的行初等变换把[A|I]变成[I|P]的形式,有很多种途径,而数值计算就是要找到一种确定性的便于计算机执行的方法,gauss jordan消元法就是这样一种方法,第i次迭代时,它让增广矩阵的第i行乘以一个系数,使得增广矩阵的第i行第i列上的元素变为1,然后让第i行以外的其他行加上第i行上对应元素的N倍,使得其他行的第i列上的元素变为0。下面举例说明gauss_jordan消元法的计算过程。
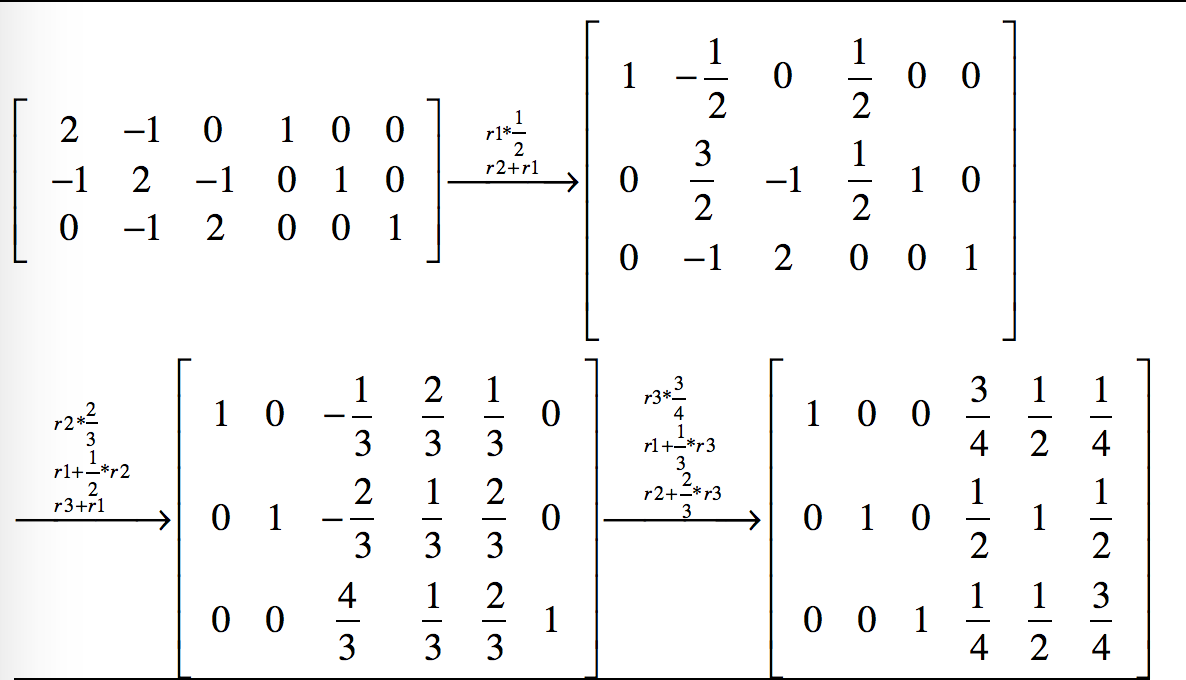
上例中A是一个3阶矩阵,所以经过3次迭代得到了它的逆矩阵,每次迭代增广矩阵中的每个元素(共3行6列18个元素)都要变一次,所以算法的时间复杂度为$O(2*n^3)$
观察上面增广矩阵的变化过程,我们发现在每一步迭代的结果中,增广矩阵左侧有x列已化为单位矩阵时,右侧就有n-x列保持着单矩阵的样子,即总能从增广矩阵中抽出n列组成一个单矩阵。同时左侧已化为单位矩阵的那几列在以后的行初等变换为始终保持不变。所以,可以把右侧不再是单位矩阵的列存储到左侧已变为单矩阵的列上,这样就不需要额外的内存来存储整个增广矩阵了,内存开销减少了一半,同时算法的时间复杂度也降为$O(n^3)$(虽然量级上没有变化)。
数值计算的迭代过程往往都伴随着舍入误差的累积,所以最终的结果也会有误差,如果这个最终的误差在一个可控的范围内,则称该算法为数值稳定的算法,否则为数值不稳定的算法。什么时候会造成数值不稳定?比如算法某一步要除以一个很小的数,小到绝对值趋近于0,商趋于无穷大,此时舍入误差大到不可控。相对于除以一个很小的数,除以一个很大数是比较安全的,因为真实的商值本来就趋于0,舍入后取0,这个误差并不大。所以gauss jordan消元法有一种“稳定”的形式,就是“选主元的gauss jordan消元法”。在每一个循环过程中,先寻找到主元(即绝对值最大的那个元素),并将主元通过行变换(无需列变换)移动到矩阵的主对角线上,然后将主元所在的行内的所有元素除以主元,使得主元化为1;然后观察主元所在的列上的其他元素,将它们所在的行减去主元所在的行乘以一定的倍数,使得主元所在的列内、除主元外的其他元素化为0,这样就使得主元所在的列化为了单位矩阵的形式。这就是一个循环内做的工作。然后,在第二轮循环的过程中,不考虑上一轮计算过程中主元所在的行和列内的元素,在剩下的矩阵范围内寻找主元。
选主元的方式虽然使算法变得非常稳定,但是计算量也明显上升,一种折中的方法是“选取列主元”,即在第i次循环迭代中,从第i列中选主元,同样第i列中第i行之前的元素不在候选的范围内。
gauss_jordan.py
# coding=utf-8
__author__ = "orisun"
import numpy as np
EPS = 1.0e-9
'''实现3种初等行变换
'''
def swapRow(A, i, j):
'''交换矩阵A的第i行和第j行
'''
n = A.shape[1]
for x in xrange(n):
tmp = A[i, x]
A[i, x] = A[j, x]
A[j, x] = tmp
def scaleRow(A, i, coef):
'''矩阵A的第i行元素乘以一个非0系数coef
'''
assert abs(coef) > EPS
n = A.shape[0]
for x in xrange(n):
A[i, x] *= coef
def addRowToAnother(A, i, j, coef):
'''把矩阵A第i行的coef倍加到第j行上去
'''
assert abs(coef) > EPS
n = A.shape[0]
for x in xrange(n):
A[j, x] = coef * A[i, x] + A[j, x]
def gauss_jordan_0(mat, column_pivot=True):
'''高斯-约旦法求矩阵的逆。
参数column_pivot为True时将采用列主元消去法。
不会改变输入矩阵mat。
时间复杂度为O(n^3)
'''
n = mat.shape[0]
# 构建增广矩阵。这样需要额外的内存空间来存储一个跟mat同等规模的矩阵
A = np.insert(mat, n, values=np.eye(n), axis=1)
for pivot in xrange(n):
if column_pivot:
# 寻找第pivot列绝对值最大的元素(即列主元),把该元素所在的行与第pivot行进行交换
if(pivot < n - 1):
maxrow = pivot
maxval = abs(A[pivot, pivot])
for row in xrange(pivot + 1, n): # 只需要从该列的第pivot个元素开始往下找
val = abs(A[row, pivot])
if(val > maxval):
maxval = val
maxrow = row
if(maxrow != pivot):
swapRow(A, pivot, maxrow)
# 第pivot行乘以一个系数,使得A[pivot,pivot]变为1
coef = 1.0 / A[pivot, pivot]
if abs(coef) > EPS:
for col in xrange(pivot, 2 * n):
A[pivot][col] *= coef
# 把第pivot行的N倍加到其他行上去,使得第pivot列上除了A[pivot,pivot]外其他元素都变成0
for row in xrange(n):
if row == pivot:
continue
coef = 1.0 * A[row, pivot]
if abs(coef) > EPS:
for col in xrange(pivot, 2 * n):
A[row, col] -= coef * A[pivot, col]
# 取出增广矩阵的右半部分即为A的逆
return A[:, n:]
def gauss_jordan(A, column_pivot=True):
'''高斯-约旦法求矩阵的逆。
参数column_pivot为True时将采用列主元消去法。
该方法经了优化,不需要额外的内存空间来存储增广矩阵。但是会改变原始的输入矩阵A,最终A变成了它自身的逆。由于没有增广矩阵,计算量至少减少为原来的一半。
时间复杂度为O(n^3)
'''
n = A.shape[0]
for pivot in xrange(n):
# 构建n行1列的B矩阵,它的第pivot行上为1,其他全为0
B = np.array([[0.0] * n]).T
B[pivot, 0] = 1.0
if column_pivot:
# 寻找第pivot列绝对值最大的元素(即列主元),把该元素所在的行与第pivot行进行交换
if(pivot < n - 1):
maxrow = pivot
maxval = abs(A[pivot, pivot])
for row in xrange(pivot + 1, n): # 只需要从该列的第pivot个元素开始往下找
val = abs(A[row, pivot])
if(val > maxval):
maxval = val
maxrow = row
if(maxrow != pivot):
swapRow(A, pivot, maxrow)
swapRow(B, pivot, maxrow)
# 第pivot行乘以一个系数,使得A[pivot,pivot]变为1
coef = 1.0 / A[pivot, pivot]
if abs(coef) > EPS:
for col in xrange(0, n):
A[pivot, col] *= coef
B[pivot, 0] *= coef
# 把第pivot行的N倍加到其他行上去,使得第pivot列上除了A[pivot,pivot]外其他元素都变成0
for row in xrange(n):
if row == pivot:
continue
coef = 1.0 * A[row, pivot]
if abs(coef) > EPS:
for col in xrange(0, n):
A[row, col] -= coef * A[pivot, col]
B[row, 0] -= coef * B[pivot, 0]
# 把B存储到A的第pivot列上去
for row in xrange(n):
A[row, pivot] = B[row, 0]
# 此时的A已变成了原A的逆
return A
def test():
import time
from numpy import random
from scipy import linalg
import math
n = 100 #n上千时用就不适合用gauss_jordan法了,半天算不出结果
arr = random.randint(100, size=(n, n))
begin = time.time()
gauss_jordan(arr, False)
end = time.time()
print 'gauss_jordan use time ', end - begin
# 矩阵规模很小时gauss_jordan法更快。矩阵规模稍大时linalg.inv更快。
# begin = time.time()
# linalg.inv(arr) #使用linalg.inv经常无法求解,因为随机构造出来的矩阵经常是奇异矩阵
# end = time.time()
# print 'linalg.inv use time ', end - begin
if __name__ == '__main__':
test()
print "original"
A = np.array([[2, -1, 0], [-1, 2, -1], [0, -1, 2]], dtype='d')
print A
print "inverse matrix"
print gauss_jordan_0(A, True)
print "inverse matrix"
print gauss_jordan(A, True)
print "swap row1 and row2"
swapRow(A, 1, 2)
print A
print "row1 multiple by -0.5"
scaleRow(A, 1, -0.5)
print A
稍大一些的矩阵求逆就不适合用gaussJordan法了(实际上很多大型矩阵的运算都不能用课本上讲的方法直接求解),大型稀疏矩阵求逆是很多论文里关注的焦点问题,常见的方法是GMRES。
说明一下通过解方程求逆矩阵的理论依据:$Ax=I$ => $A(x_1|x_2|...|x_n)=(I_1|I_2|...|I_n)$ => $Ax_1=I_1,\ Ax_2=I_2,\ Ax_n=I_n$
其中$x_i$是矩阵$x$的第i列,$I_i$是单位矩阵$I$的第i列。$x=A^{-1}$。我们可以解一次方程$Ax=I$直接得到$x$,但这种“省事”的方法可能产生内存溢出。我们也可以解n个方程$Ax_1=I_1,\ Ax_2=I_2,\ Ax_n=I_n$,最后把$x_i$拼在一起构成$x$,这样不存在内存溢出的问题,但是计算十分耗时。折中的方法是每次解方程求出$x$的一部分,即解$Ax_{i...j}=I_{i...j}$
solve_matrix.py
# coding=utf-8
__author__ = "orisun"
import numpy as np
from scipy.linalg import lu, solve # 建议使用scipy.linalg取代numpy.linalg
from scipy.sparse import lil_matrix, dok_matrix, coo_matrix
from scipy.sparse.linalg import gmres, lgmres, spsolve, inv # 专门用来求解稀疏系数矩阵方程组
import time
from numpy import random
if __name__ == '__main__':
n = 1000 # 上万维时LU分解直接内存溢出
arr = random.random(size=(n, n))
begin = time.time()
x, l, u = lu(arr) # LU分解
end = time.time()
print 'LU decomposition use time ', end - begin
# 二维矩阵建议使用numpy.array,不要使用numpy.matrix
A = np.array([[2, -1, 0], [-1, 2, -1], [0, -1, 2]], dtype='d')
b = np.eye(3)
print '解方程', solve(A, b) # 通过解方程的方式也可以求逆
print '解方程', spsolve(A, b) # 稀疏矩阵解方程
print '求逆', inv(lil_matrix(A)) # 稀疏矩阵求逆(要求原矩阵必须非奇异)
b = np.array([[1, 0, 0]]).T
print '解方程', gmres(A, b, tol=1e-08, maxiter=1)[0] # 稀疏矩阵解方程
print '解方程', lgmres(A, b, tol=1e-08, maxiter=1)[0] # lgmres比gmres收敛性好一些
print
# 使用spsolve解方程的方式对大型稀疏矩阵求逆(原矩阵可以是奇异的)
n = 7000
arr = lil_matrix((n, n))
arr[0, 165] = 1.0
arr[135, 138] = 1.0
arr[545, 388] = 1.0
arr[998, 578] = 1.0
arr[13, 455] = 9.0
b = np.eye(n)
begin = time.time()
spsolve(arr, b) # 稀疏矩阵解方程
end = time.time()
print 'spsolve use time ', (end - begin) # n=7000时耗时1秒
捎带说一句,求逆矩阵另外一种常用的方法是LU分解,时间复杂度跟Gauss-Jordan法相同,都是$n^3$。如果只是做矩阵分解,LU分解法大约需要执行$\frac{n^3}{3}$次内层循环(每次包括一次乘法和一次加法)。这是求解一个(或少量几个)右端项时的运算次数,它要比Gauss-Jordan消去法快三倍,比不计算逆矩阵的Gauss-Jordan法快1.5倍。当要求解逆矩阵时,总的运算次数(包括向前替代和回代部分)为$n^3$,与Gauss-Jordan法相同。
本文来自博客园,作者:张朝阳讲go语言,转载请注明原文链接:https://www.cnblogs.com/zhangchaoyang/articles/5471608.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号