\begin{equation}\begin{aligned}
\min \quad & z=\mathbf{c}^{T} \mathbf{x} \\
\text { s.t. } & \mathbf{A} \mathbf{x}=\mathbf{b} \\
& \ell \leq \mathbf{x} \leq \mathbf{u}
\end{aligned}\end{equation}
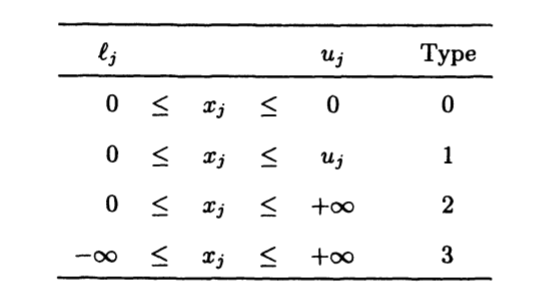
The types of the components
of x are defined as
\begin{equation}
\begin{aligned}
&\mathcal{U}=\left\{k: k \in \mathcal{R}, x_{k}=u_{k}\right\}\\
&\mathcal{M}=\left\{i: x_{k_{i}}<0, i \in \mathcal{I}_{0} \cup \mathcal{I}_{1} \cup \mathcal{I}_{2}\right\}\\
&\mathcal{P}=\left\{i: x_{k_{i}}>u_{k_{i}}, i \in \mathcal{I}_{0} \cup \mathcal{I}_{1}\right\}\\
&\mathcal{F}=\mathcal{I} \backslash(\mathcal{M} \cup \mathcal{P})
\end{aligned}
\end{equation}
Using notation $\beta = x_{\mathcal{B}}$ we can simplify the reference to basic variables. As a measure of infeasibility we use the negative of the sum of violations:
$$w=\sum_{i \in \mathcal{M}} \beta_{i}-\sum_{i \in \mathcal{P}}\left(\beta_{i}-v_{i}\right)$$
Obviously, $w \geq 0$. If $w = 0$ then both $\mathcal{M}$ and $\mathcal{P}$ are empty and the
solution is feasible.
So it is translated into
\begin{equation}\begin{aligned}
\max \quad & w \\
\text { s.t. } & \mathbf{A x}=\mathbf{b} \\
& \ell \leq \mathbf{x} \leq \mathbf{u}
\end{aligned}\end{equation}
We can investigate how feasibility of the basis is affected if a nonbasic
variable is displaced by t in the feasible direction. First, assume the
displacement is nonnegative, $t \geq O$. The i-th basic variable as a function of t is
$$\beta_{i}(t)=\beta_{i}-t \alpha_{q}^{i}$$
$\boldsymbol{\alpha}_{q}=\mathbf{B}^{-1} \mathbf{a}_{q}, \boldsymbol{\beta}=\mathbf{B}^{-1} \mathbf{b}_{\mathcal{U}}, \boldsymbol{\beta}(t)=\mathbf{x}_{\mathcal{B}}(t)$.
Given $\mathcal{M} \cup \mathcal{P} \neq \emptyset$ and $j \in \mathcal{R}$ with . w can be
improved by increasing the value of $x_{j}$ only if
$$d_{j}=\sum_{i \in \mathcal{M}} \alpha_{j}^{i}-\sum_{i \in \mathcal{P}} \alpha_{j}^{i}<0$$
If the infeasibility sets M and P remain unchanged only for t = 0
then the basis is degenerate.
A feasible displacement of a variable can also be negative. In this
case, w can be improved by decreasing Xj if $d_j >0$.
Define vector h with components
$$h_{i}=\left\{\begin{array}{ll}
1, & \text { if } i \in \mathcal{M} \\
-1, & \text { if } i \in \mathcal{P} \\
0, & \text { otherwise }
\end{array}\right.$$
It is easy to see that
$$d_{j}=\mathbf{h}^{T} \boldsymbol{\alpha}_{j}=\mathbf{h}^{T} \mathbf{B}^{-1} \mathbf{a}_{j}$$
just like the
phase-2 simplex multiplier $\pi$, by
$$\boldsymbol{\phi}^{T}=\mathbf{h}^{T} \mathbf{B}^{-1}$$
Define
$$\begin{array}{l}
K^{-}=\left\{\begin{array}{ll}
0, & \text { if } K \geq 0 \\
K, & \text { if } K<0
\end{array}\right. \\
K^{+}=\left\{\begin{array}{ll}
K, & \text { if } K>0 \\
0, & \text { if } K \leq 0
\end{array}\right.
\end{array}$$
The measure of infeasibility as a function of t can be expressed as
$$\begin{aligned}
w(t) &=\sum_{i \in \mathcal{I}_{\ell}}\left[\beta_{i}(t)\right]^{-}-\sum_{i \in \mathcal{I}_{u}}\left[\beta_{i}(t)-v_{i}\right]^{+} \\
&=\sum_{i \in \mathcal{I}_{\ell}}\left[\beta_{i}-t \alpha_{i}\right]^{-}-\sum_{i \in \mathcal{I}_{u}}\left[\beta_{i}-t \alpha_{i}-v_{i}\right]^{+}
\end{aligned}$$
where $\mathcal{I}_{\ell}=\mathcal{I}_{0} \cup \mathcal{I}_{1} \cup \mathcal{I}_{2}$ (index set of basic variables with 0 lower bound) and $\mathcal{I}_{u}=\mathcal{I}_{0} \cup \mathcal{I}_{1}$
(basic variables with finite upper bound).
Analysis of w(t)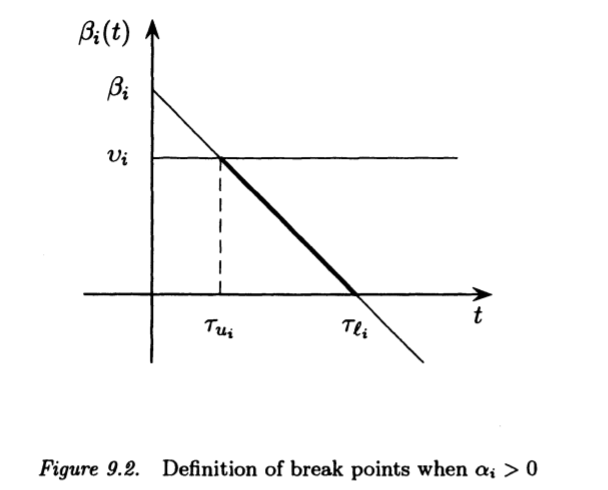

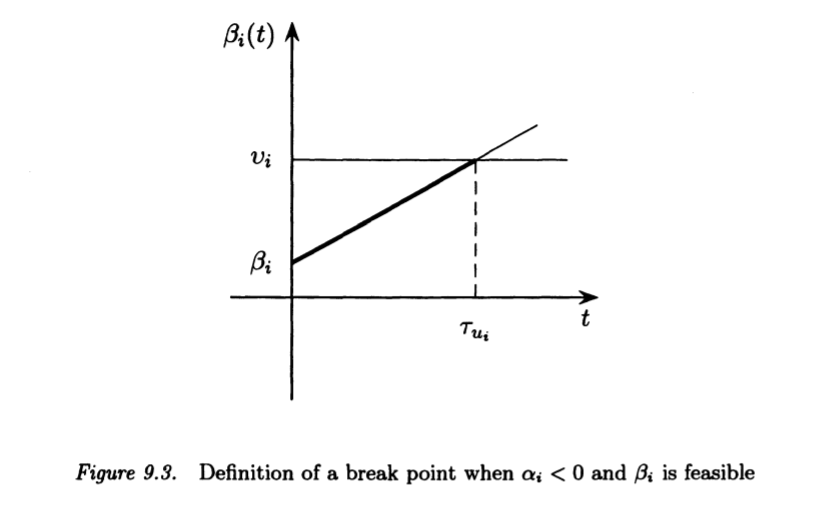
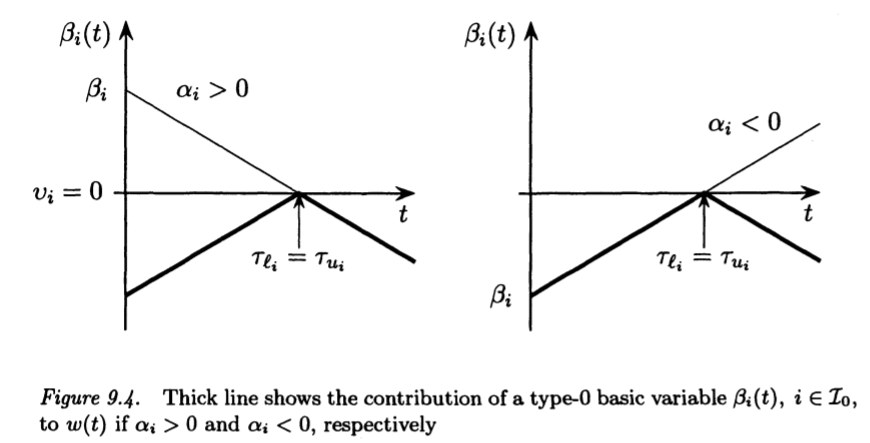
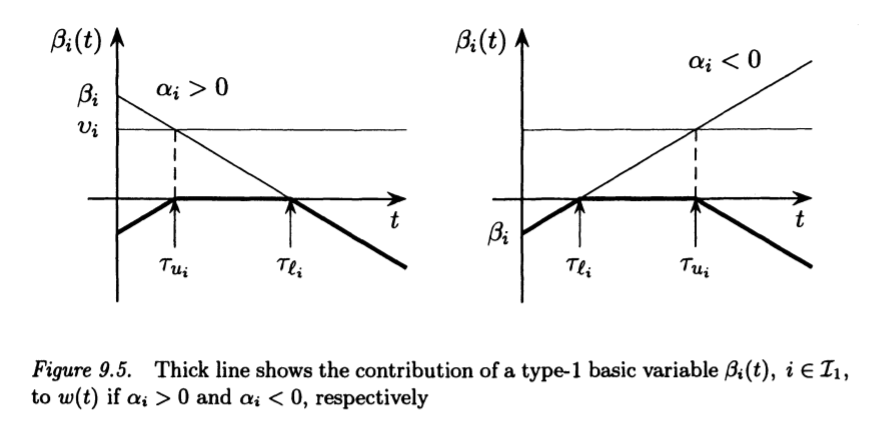
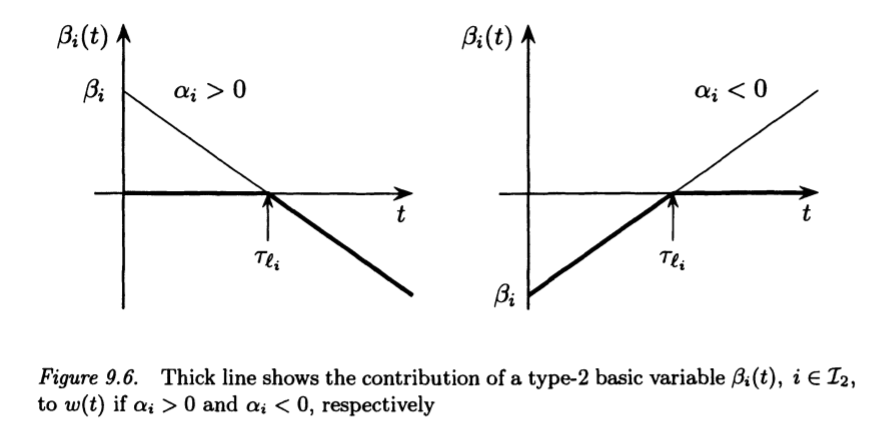
The contribution of the $\beta_{i}(t)$ to $w(t)$ is illustrated
in figures 9.4, 9.5 and 9.6.
When t moves away from 0 in the positive direction the first change in
the feasibility status of one of the basic variables occurs when t reaches
the first break point. It is the smallest of the ratios defined in (9.87) and
(9.88). Since we want to pass this point and want to do further steps we
assume that the break points are sorted into ascending order:
$$0 \leq t_{1} \leq \cdots \leq t_{S}$$
t if $x_q$ is the selected improving variable
coming in from lower bound then the rate of change of $w(t)$ is $-d_q$. Therefore, in the [0, tIl interval w(t) increases by -dqtl.
Denoting
$$r_{1}=-d_{q}=-\left(\sum_{i \in \mathcal{M}} \alpha_{i}-\sum_{i \in \mathcal{P}} \alpha_{i}\right)$$
$$r_{k+1}=r_{k}-\left|\alpha_{j_{k}}\right|, \quad k=1, \ldots, S$$
The maximum of w(t) is defined by index s for which
$$\begin{array}{lll}
r_{s}>0 & \text { and } & r_{s+1} \leq 0
\end{array}$$
$$w\left(t_{k}\right)=w\left(t_{k-1}\right)+\left(t_{k}-t_{k-1}\right) r_{k}, \quad k=1, \ldots, s$$



 浙公网安备 33010602011771号
浙公网安备 33010602011771号