信息安全与密码技术

 

古罗马：Caesar 密码 c=( m+ 3) Mod 26

 

 三个发展阶段

保密：搭线窃听和密码分析

保护：保护信息的机密性、完整性和可用性

保障：可认证性，不可否认性

 

信息安全的基本属性

 机密性（Confidentiality）：信息不泄露给非授权的个人、实

体或进程，不为其所用。

 完整性（Integrity）：维护信息的一致性，即信息在生成、传

输、存储和使用过程中不应发生人为或非人为的非授权篡改。

 可用性（Availability）：保障信息资源随时可提供服务的能力

特性，即授权用户根据需要可以随时访问所需信息。

 可认证性（Authenticity）：能够核实和信赖一个合法的消息源

的真实性的性质，以建立对其的信任。

 不可否认性（Non-repudiation）：保证信息的发送者提供的交

付证据和接受者提供的发送者证据一致，使其以后不能否认信息

过程。

 

加密和解密的数学函数

c=E(m), m=D(c) , D(E(m))= m

 

密钥(Key) :算法中的一个变量

c=EKe(m), m=DKd(c) , DKd(EKe(m))= m

 

密码系统的两个基本单元是算法和密钥。

 

算法是相对稳定的，视为常量。

密钥则是不固定的，视为变量。

密钥安全性是系统安全的关键。

 

 

密码攻击

在未知密钥的前提下，从密文恢复出明文、或者推导出密钥

对密码进行分析的尝试称为攻击

 

攻击方法分类（根据已知信息量的多少）

• – 唯密文攻击
• – 已知明文攻击
• – 选择明文攻击
• – 自适应选择明文攻击
• – 选择密文攻击
• – 选择密钥攻击

 方法

穷举：用各种可能

分析：通过数学关系式或统计规律找出明文或与明文相关的有用信息

 

 

密码算法的安全性

1. 破译算法的代价　　>　　加密数据本身的价值

1. 在信息的生命期内无法破解

 

 

 

对称密钥密码体制

加密密钥与解密密钥是相同的或从一个容易推出另一个。

 

 

 

 

组密码：将明文分成固定长度的组，典型的分组密码算法为：DES算法和AES算法。

序列密码/流密码：每次加密一位或一字节的明文，典型的现代序列密码是由RSA公司发明的RC4。

 

 

 

rsa算法

 

n = p q 

m = (p-1) (q-1)

1< e < m　　　　e与m互质

(e * d ) % m = 1。

公钥为 （n，e)

私钥　（n，d)

 

加密　　a 为明文，b 为密文

a^e % n = b

 

解密

a^d % n = b

 

 欧几里得算法（辗转相除法）

123456 和 7890 的最大公因数是 6，这可由下列步骤（其中，“a mod b”是指取 a ÷ b 的余数）看出：

 

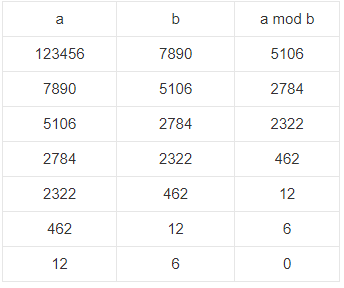
扩张欧几里得算法的解：

def ext_euclid(a, b):
    if b == 0:
        return 1, 0, a
    else:
        x, y, q = ext_euclid(b, a % b)
        # q = gcd(a, b) = gcd(b, a%b)
        x, y = y, (x - (a // b) * y)
        return x, y, q

 

 

 

 base64

 

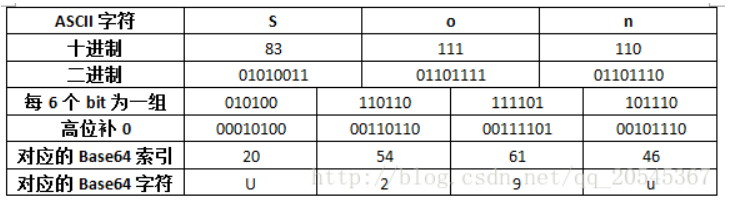
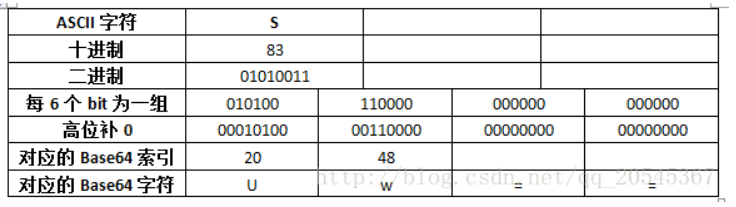
 base64加密与解密

encode = base64.b64encode(b'I love you')　　　　　　　　　　　　　　#加密
decode = base64.b64decode(b'SSBsb3ZlIHlvdQ==')　　　　　　　　　　#解密

 

 base32加密与解密

encode = base64.b32encode(b'I love you')　　　　　　　　　　#加密
decode = base64.b32decode(b'JEQGY33WMUQHS33V')　　　　　　#解密