论文解读-《Higher-Order Expander Graph Propagation》

1. 论文介绍

论文题目：Higher-Order Expander Graph Propagation
论文领域：图神经网络
论文发表：NIPS 2023
论文背景：

2. 论文摘要

图神经网络通过沿边交换信息来处理图结构数据。这种消息传递范式的一个限制是过度挤压问题。当来自节点扩展的感受野的消息被压缩成固定大小的向量时，会发生过度挤压，这可能会导致信息丢失。为了解决这个问题，最近的工作探索了使用扩展图来执行消息传递，扩展图是具有低直径的高度连通的稀疏图。然而，现有的扩展图传播方法只考虑成对相互作用，忽略了复杂数据中的高阶结构。为了探索在仍然利用扩展图的情况下捕获这些高阶相关性的好处，我们引入了高阶扩展图传播。我们提出了两种构造二部展开器的方法，并评估了它们在合成数据集和真实数据集上的性能。

3. 相关介绍

3.1 背景介绍

扩展图在信息传播方面具有多项优势特性，如稀疏性、高连通性和对数级直径，这些特性使得信号能够以最少的消息传递步骤在图中高效传播。

过度挤压
解决过度挤压问题的来源有两种，空域的和谱域的。空域的方法主要针对减少两两节点的距离，具体实现是添加显式边，利用高阶结构，或通过注意力机制重新加权。谱域的方法主要针对提高图的Cheeger常量，减小图瓶颈的度量，比如基于Lovasz边界的优化，一阶谱重连，扩展器图的使用。

扩展器
扩展图因其良好的谱特性而受到关注，被视为缓解图神经网络中过度挤压问题的一种手段。4-正则Cayley图被用作输入图与扩展图之间消息传递的交错模板。与此同时，另一种方法采用了基于扩展图构建的随机局部边翻转算法。我们的工作在此研究基础上展开，重点利用二分扩展图捕捉节点间的高阶交互作用。

3.2 理论背景

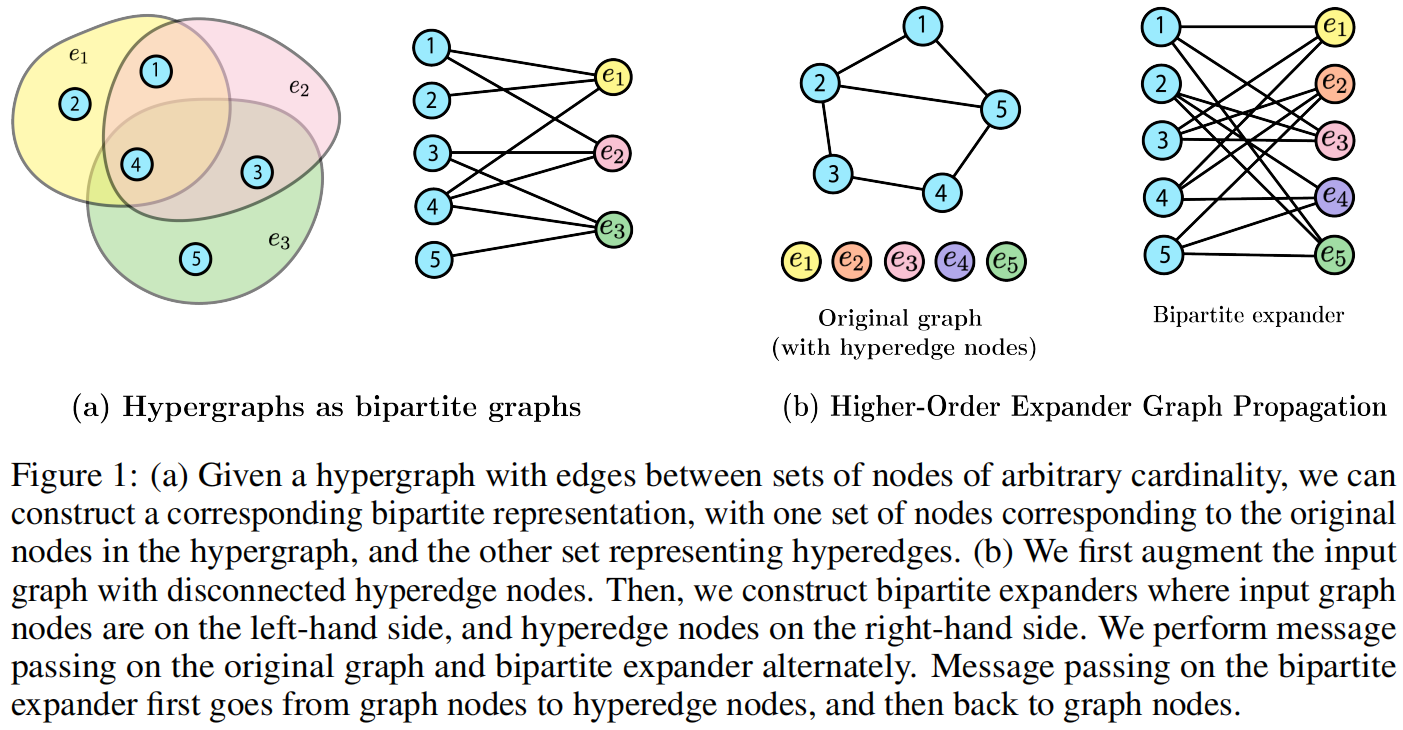
超图H=(V, E)是图的一种广义形式，其边可以发生在任意大小的节点集合之间。若每条超边的基数均为k，则称该超图为k-均匀超图。
二分图（Bipartite graphs），记作 B = (L, R, E)，是指其顶点可划分为两个互不相交的集合 L 和 R，且同一集合内的节点之间不存在边相连的图。
超图可以表示为二分图：二分图中的一组节点（称为L）对应于超图中的原始节点，而另一组节点（R）则代表超边。二分图表示在图表示学习中特别有用，它使得人们能够将针对标准图开发的一系列工具稍作调整即可应用于超图上。

4. 扩展器图理论分析

扩展器图是一个稀疏图且有一个低的直径，所以在扩展器图上进行消息传递可以克服过度挤压问题。定义k-正则扩展器图

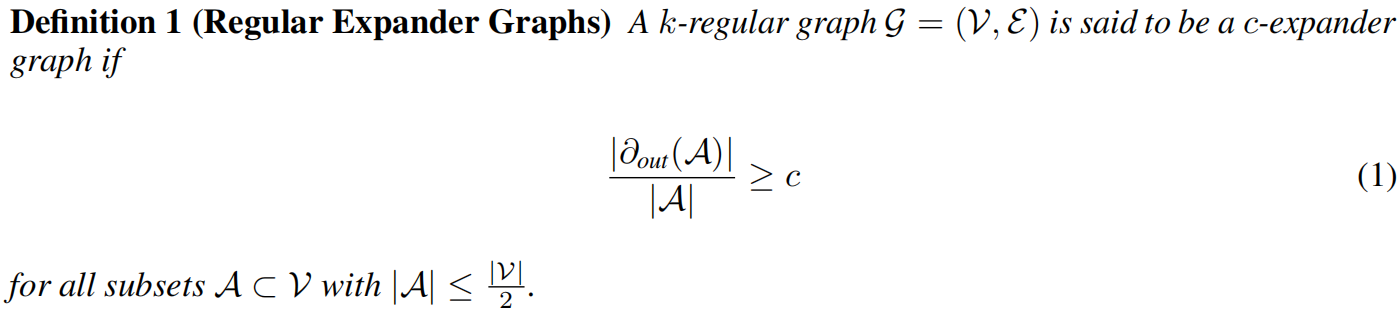
有很多方法可以去构建扩展器图，如基于代数原理的使用Cayley图构建确定性的图。还有一些是基于Ramanujan（拉马努金图）图族，这类图具有特殊的光谱特性，使其成为扩展图的绝佳候选。

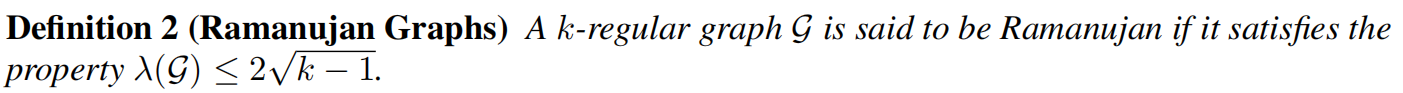
其中最大幅度的非平凡特征值为

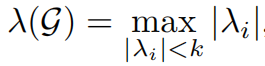
这个定义说明了Ramanujan图天然有小的直径。

对于k正则的图的直径的边界为

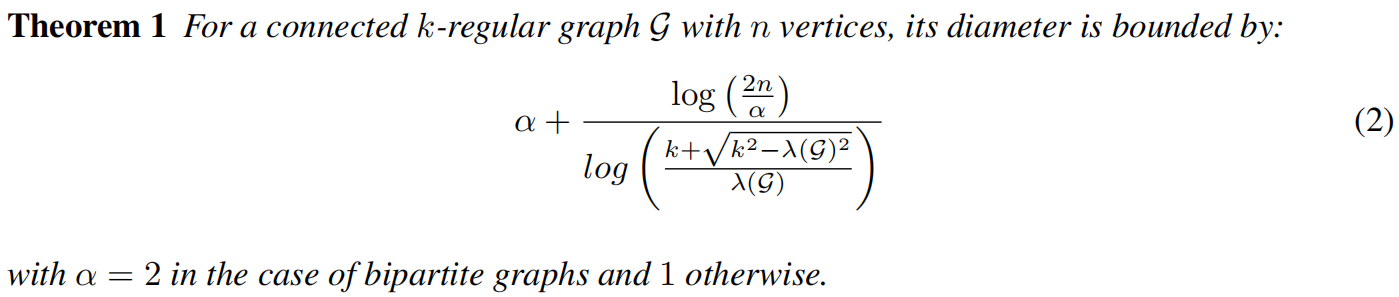
为了最小化图的直径，必须最小化λ(G)，引出定理

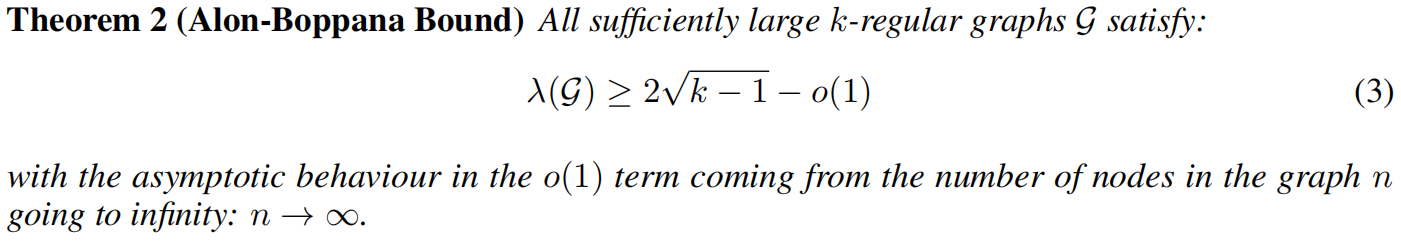
因此，拉马努金图具有λ(G)的最小可能值，从而实现了渐进最小直径。这一特性可进一步与定义1中所述的生成图扩展常数c相关联。

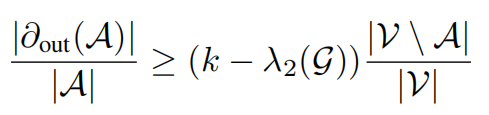
显然，拉马努金图是具有低直径和高扩展常数的优秀扩展图。
此外，即便是k-正则图也能成为良好的扩展图。关于扩展图的另一种定义涉及边扩展率h(G)：给定顶点子集A⊆V，其边的边界，指一端在A内、另一端在A外的边集合。由此，扩展图的替代定义可表述如下。

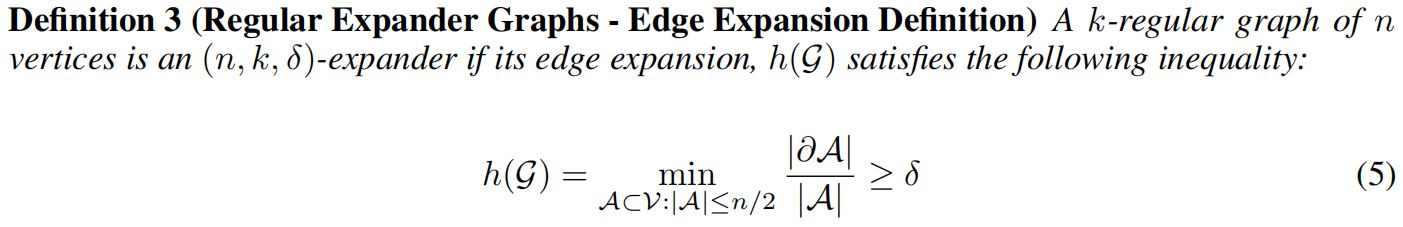
引入另一个定理给出了k-正则图中δ的下界：

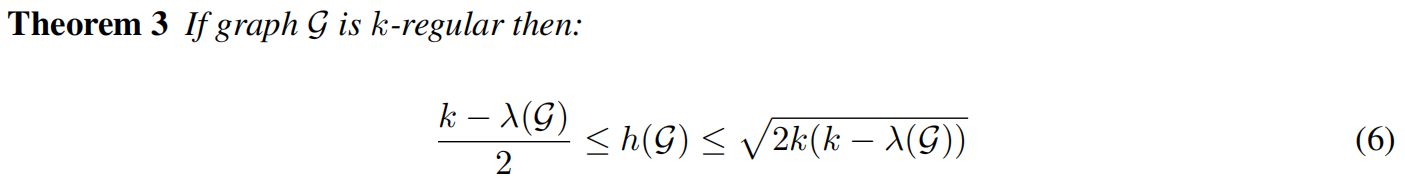
5. 高阶扩展器图传播

首先在二分图扩展器的定义上，来引入匹配的定义。
定义：匹配：图的一个匹配是一个没有共同节点的边的集合。
定义：完美匹配：图的一个完美匹配是包含图中所有节点的匹配。
随机Ramanujan二分图，为了产生随机k-正则图之外，检验扩展器是否符合Ramanujan的属性，需要使用O(|V|3)的时间复杂度来检查图邻接矩阵的特征值。

5.1 HEGP算法架构

如图1b所示
第一步，给定一个初始的图G，首先用|V|个超边节点对其进行扩充，称之为集合H。基于V和H建立一个二分扩展器图 B = (L, R, E) 其中令L = V和R = H。
第二步，我们通过构建一组边E来连接两侧的节点，具体采用完美匹配或拉马努金图的方式。
这样就得到了一个k-正则的二分扩展器图，k是一个超参数。

第三步，为了在不丢失原始图拓扑结构的情况下将扩展图融入模型，参照EGP的方法，通过在两个图上交替进行消息传递。因此，我们在奇数层对原始图执行消息传递，在偶数层对扩展图执行消息传递。
第四步，最后，在执行图池化操作时，我们忽略了所有来自超边节点的特征，这意味着仅使用输入图中的节点表示来预测最终的图分类结果。

二分扩展器图的消息传递
原始图和二分扩展器图的交替叠加，信息在两个层之间来回传递，这种设计使得每个超边节点能够充当k个图节点的通信枢纽，从而实现超越成对交互的高阶消息传递。
在实际实验中，超边节点特征初始化为全零值。在消息传递过程中，我们测试了两种处理方法：

• 一种允许超边节点特征进行端到端学习，
• 另一种则仅通过求和运算聚合来自原始图节点的消息至超边节点，随后接入一个线性层。

6. 实验设置

基线模型：使用GIN，通过对最终GIN层后的节点表征进行平均来实现图级池化，随后使用特定任务的损失函数来评估图分类结果。

本文模型，采用两种二分扩展器图，一类是扩展器图为完美匹配，另一类是使用Ramanujan图。
此外，我们测试了两种处理任意超边节点特征的方法，具体取决于这些特征是学习得到的（学习特征）还是通过求和聚合的（求和特征）。

数据集
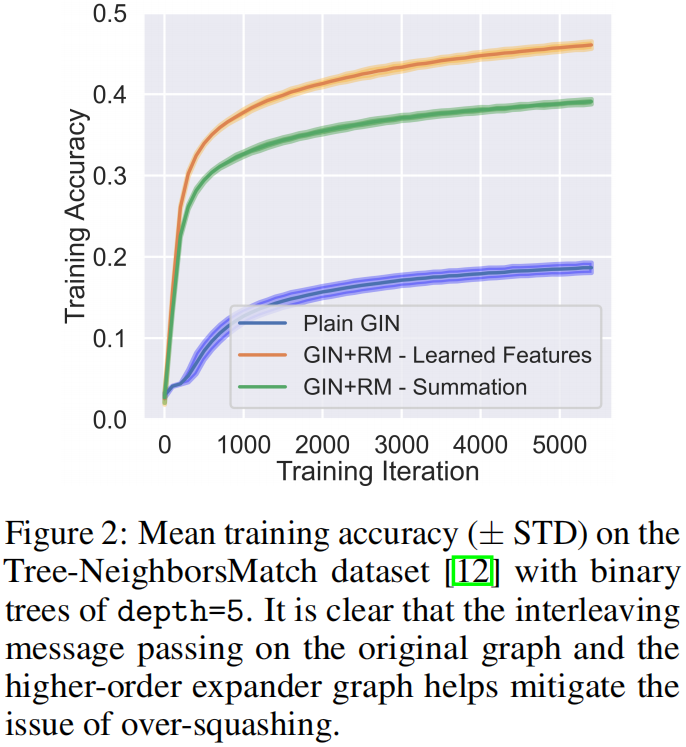
Tree-NeighborsMatch数据集
其中二分扩展图的正则系数被设定为k = 3，效果如图，在原始图和二分扩展图之间交替进行消息传递，有助于缓解过度挤压问题。

OGB数据集
在ogbg-molhiv数据集上使用5正则的二分扩展器图

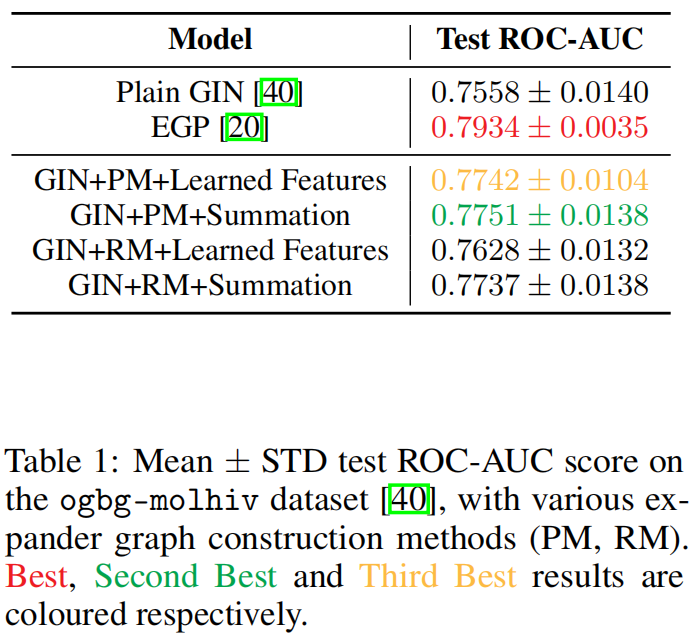
如图，GIN+完美匹配+超边节点特征的求和处理，获得了最好的效果。
有趣的是，没有任何策略能达到原始扩展图EGP论文中的性能表现。我们认为这可能是因为高阶相互作用在ogbg-molhiv数据集中并无实际作用，亦或是由于我们对超边节点特征学习方式的处理所致。
同时，Ramanujan图并没有获得最好效果。这可能表明，强制实施Ramanujan拉马努金图并不会带来明显的性能提升，其效果仅相当于使用普通的k-正则二分扩展图。

OGB-code2数据集

本文的算法获得了最好效果。一种可能解释是，高阶交互作用可能对该任务有所帮助，从而使得我们的方法产生优势。

7. 核心代码

# 使用完美匹配的方式进行生成二分扩展器图
def add_expander_edges_via_perfect_matchings(hypergraph_order: int,
                                             dataset: str,
                                             data: Data):
    """
    Augments graph in 'data' with a new bipartite graph representation of a hypergraph for use as an expander graph.
    For each node in the original graph, we add a node in the bipartite graph. We then generate 'hypergraph_order'
    disjoint perfect matchings of the resulting bipartite graph, and store these edges in the 'expander_edge_index' attribute
    of the 'data'. We add the expander graph 'edge nodes' to the original graph nodes in 'data.x', and add an
    'expander_node_mask' attribute, where expander_node_mask[i] == 1 if data.x[i] is a node belonging to the original
    graph, and is 0 if data.x[i] is an 'edge node' belonging to the expander graph.

    :param hypergraph_order: number of perfect matchings to generate. This is the order of the resulting 'hypergraph'.
    :param dataset: dataset which is being augmented
    :param data: graph to be augmented
    :return: updated graph with additional attributes for expander graph
    """
    if dataset == "ppa":
        # ppa dataset requires manual addition of node features
        data.x = torch.zeros(data.num_nodes, dtype=torch.long)
    new_data = data
    num_nodes = data.x.shape[0]
    expander_graph_edge_nodes = torch.zeros(data.x.shape, dtype=data.x.dtype)
    expander_graph_x = torch.concat((data.x, expander_graph_edge_nodes))
    new_num_nodes = expander_graph_x.shape[0]

    destination_node_permutations = []
    # Generate `hypergraph_order` disjoint perfect matchings
    for matching_num in range(hypergraph_order):
        disjoint_matching = False
        destination_nodes = torch.tensor([num_nodes + j for j in range(num_nodes)])
        while not disjoint_matching:
            rand_perm = torch.randperm(destination_nodes.shape[0])
            destination_nodes = destination_nodes[rand_perm]
            if num_nodes < hypergraph_order:
                # If there are fewer nodes than the order of the hypergraph, we can't avoid duplicate edges in the
                # constructed bipartite graph
                disjoint_matching = True
            else:
                # Checks to ensure that the matching is disjoint to all previous
                # matchings so that the generated hypergraph is regular
                disjoint_matching = True
                for i in range(matching_num):
                    disjoint_matching = disjoint_matching and (destination_nodes != destination_node_permutations[i]).all()
                    if not disjoint_matching:
                        break
        destination_node_permutations.append(destination_nodes)

    all_destination_nodes = torch.hstack(destination_node_permutations)
    all_source_nodes = torch.randperm(num_nodes)
    all_source_nodes = all_source_nodes.repeat(hypergraph_order)

    expander_edge_index = torch.cat((all_source_nodes[None, ...], all_destination_nodes[None, ...]), dim=0)
    expander_edge_index = coalesce(expander_edge_index)  # Remove duplicate edges
    if num_nodes >= hypergraph_order:
            # If there are more (or equal) nodes in the original graph than the hypergraph order, then there should
            # be 'hypergraph_order' * 'num_nodes' unique edges in the graph
            assert expander_edge_index.shape[1] == hypergraph_order * num_nodes

    ones = torch.ones(num_nodes)
    zeros = torch.zeros(num_nodes)
    expander_node_mask = torch.concat((ones, zeros))
    new_data['expander_edge_index'] = expander_edge_index
    new_data['expander_node_mask'] = expander_node_mask
    new_data['x'] = expander_graph_x
    new_data['num_nodes'] = new_num_nodes
    if dataset == "code2":
        # In code2 nodes have an additional "node_depth" feature. We set this to 0 for the expander graph edge nodes, but
        # it could be initialised to any value as these nodes have their features set to 0 at the start of training.
        expander_graph_edge_node_depths = torch.zeros(data.node_depth.shape, dtype=data.node_depth.dtype)
        expander_graph_node_depths = torch.concat((data.node_depth, expander_graph_edge_node_depths))
        new_data['node_depth'] = expander_graph_node_depths
    return new_data

8. 总结和个人感想

理论分析了很详细， 但是在实验结果上过于简单，并没有充分证明高阶EGP算法的有效性。仅仅从理论证明了算法的可行。