论文解读-《Deep Graph Infomax》
1. 论文介绍
论文题目:Deep Graph Infomax
论文发表: ICLR 2019
论文领域:图神经网络,无监督学习
论文背景:

2. 论文摘要
我们提出了深度图Infomax(DGI),这是一种以无监督方式学习图结构数据中节点表示的通用方法。DGI依赖于让局部表示和相应的图高阶的摘要信息之间的互信息最大化,这两者都是使用已建立的图卷积网络架构导出的。学习到的局部表示总结了以感兴趣节点为中心的子图,因此可以重新用于下游的节点学习任务。与大多数先前使用GCN进行无监督学习的方法相比,DGI不依赖于随机游走目标,并且很容易适用于转导和归纳学习设置。我们在各种节点分类基准上展示了具有竞争力的性能,有时甚至超过了监督学习的性能。
3. 相关工作
近期,通过互信息神经估计(MINE)这一方法,互信息的可扩展性估算变得既可行又实用。该技术依赖于训练一个统计网络,使其能够区分来自两个随机变量联合分布的样本与其边缘分布乘积的样本。
概率论和信息论中,两个随机变量的互信息(Mutual information,MI)是指变量间相互依赖性的度量。
目前还没有工作把互信息最大化引入图结构领域,本文将DIM引入图领域。
3.1 对比学习
对比学习方法是采用一个计分函数,训练编码器来实现对正样本的增分,对负样本的减分。
DGI在这方面同样采用对比方法,因为我们的目标基于对局部-全局配对和负采样对应项进行分类。
3.2 采样策略
关键的实现是对比学习的如何采样正负样本,之前的方法基于局部的对比损失函数。
3.3 预测编码
对比预测编码CPC是基于互信息最大化的学习深度特征的方法。CPC与上述图方法均具有预测性:对比目标有效地训练了输入中结构指定部分之间的预测器(例如相邻节点对之间或节点与其邻域之间)。
我们的方法不同之处在于同时对比图的全局/局部部分,其中全局变量由所有局部变量计算得出。
目前对比图的全局和局部特征的方法都是基于邻接矩阵或将区域级约束融入特征空间的方法,这两种方法都是基于矩阵分解,所以不适用于大图。
4. DGI方法
整个DGI包括三个模块,特征提取器,聚合器,判别器
4.1 特征提取器
需要从图数据中提取到特征,需要节点特征和节点间的邻接矩阵信息,
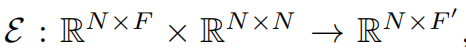
根据上面的编码器有
$$ ε(X, A) = H = {h_1, h_2, ..., h_N} $$
4.2 readout函数
为了获得图级别的摘要信息,使用readout函数
$$ R: R^{NXF} -> R^F $$
将所有的局部特征聚合成为一个固定大小的总向量s。
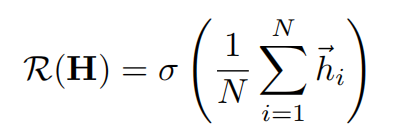
4.3 判别器
为了最大化本地互信息,使用判别器D,对所有的局部特征-全局摘要的pair进行表征一个概率得分。(对于局部特征在全局特征内部的pair,得分更高)
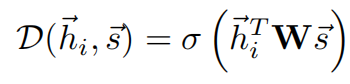
其中w是可学习权重,σ是sigmoid非线性函数
4.4 负样本获取
对于单个图来说,使用随机的污染函数在原始图中获得一个负样本
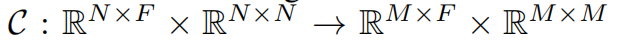
4.5 整个DGI训练的损失函数
从DIM的灵感,采用噪声对比型目标函数,通过标准二元交叉熵(BCE)损失来衡量联合分布样本(正例)与边缘分布乘积样本(负例)之间的差异。

该方法是基于詹森-香农散度2,可以有效最大化hi与s之间的互信息,通过计算联合分布与边缘分布乘积之间的差异实现。
在节点分类任务中,我们的目标是让各个图块与图中相似的图块建立连接,而非强制要求摘要包含所有这些相似性(不过这两种效果原则上应该会同时发生)。
4.6 理论分析
判别器的分类误差和图特征的互信息最大化程度的联系
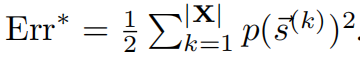
首先定义最大的信息为,(MI是互信息函数)

定义图节点的k阶的邻居映射得到的高阶特征
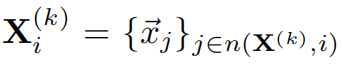
那么经过编码器函数得到的特征为
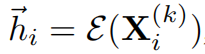
假设有
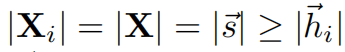
所以有最小化分类误差,即p(h, s)和p(h)p(s)之间的距离最小化,就是最大化S
4.7 DGI算法架构
整体的架构图如下
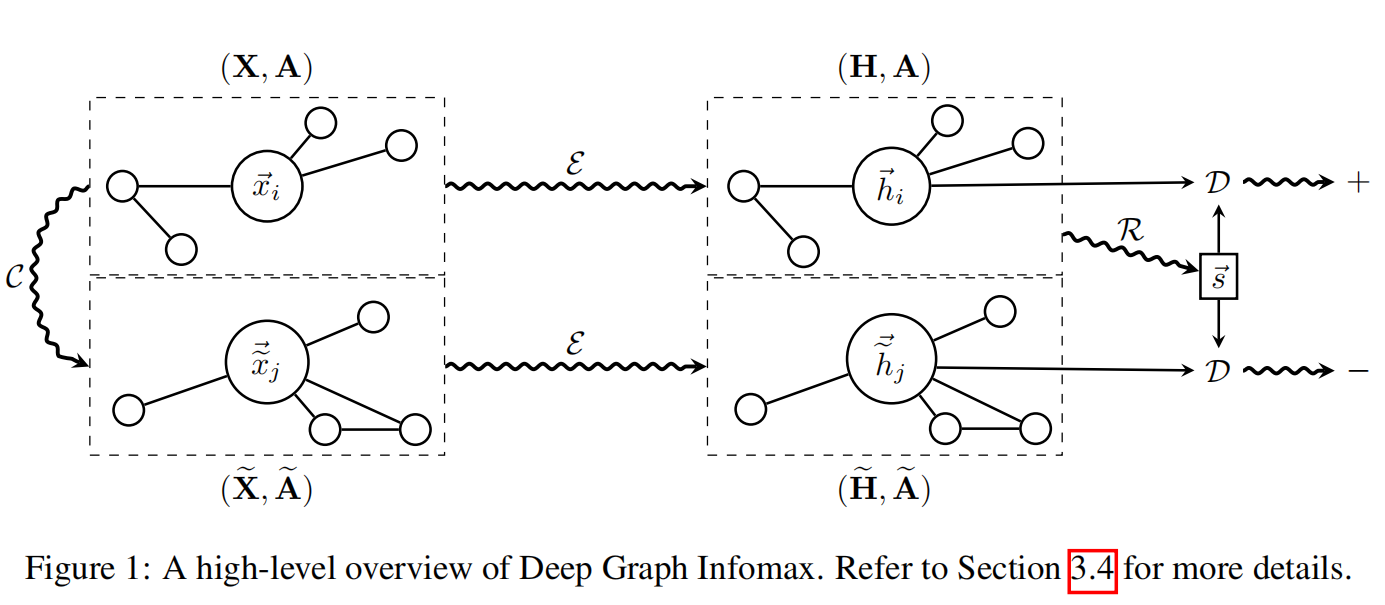
详细的步骤解释为
- 1,使用污染函数获取一个负样本
![dgi13]()
- 2,根据编码器,输入原始图来来获得局部特征hi
- 3,根据编码器,输入负样本来获得局部特征hj
- 4,对于两个局部特征,分别跟原始图通过readout函数获得摘要
- 5,根据梯度信息来更新参数,以最大化互信息量。
5. 实验设置
5.1 基础比较
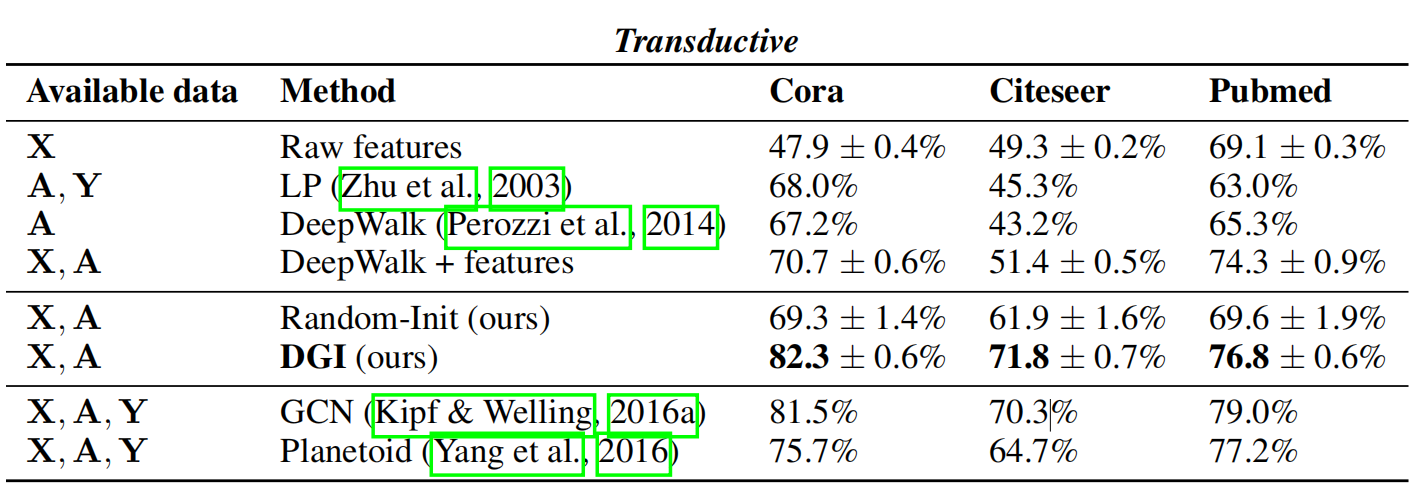
数据集分为三类:研究型论文数据 cora,citeseer 和 pubmed;社交网络数据 Reddit posts;蛋白质结构数据(PPI)
评价指标:分类准确率(直推式学习)和F1分数(归纳式学习)
对比方法:DeepWalk ,GCN,Label Propagation,Planetoid
直推式数据结果
归纳式学习的实验结果
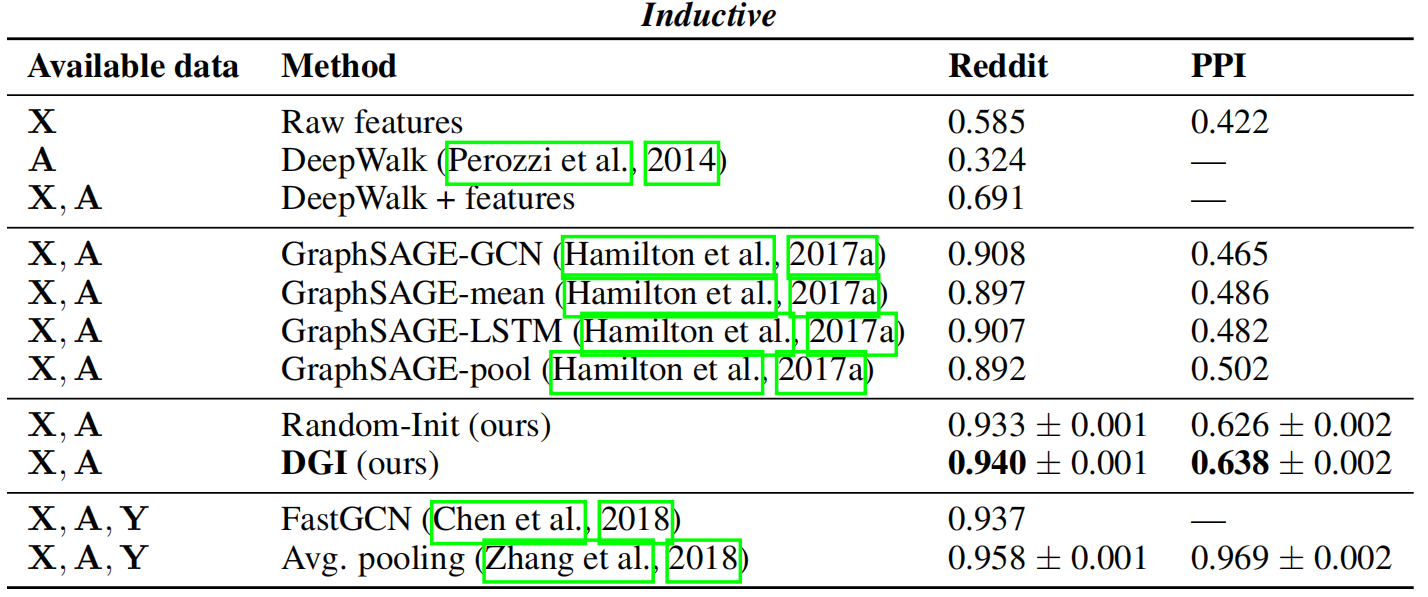
5.2 在实验中发现
更深的编码器会导致生成的局部特征表征之间产生更显著的混合,从而降低我们正负样本池的有效变异性。
我们认为这正是较浅层架构在某些数据集上表现更优的原因。虽然无法断言这些趋势具有普适性,但通过DGI损失函数,我们普遍发现采用更宽而非更深的模型能带来性能提升。
5.3 定性分析
在cora数据集上将产生的数据特征进行二维映射,得到效果图

我们进行了更深入的分析,揭示了DGI学习机制的内在原理:通过隔离带有偏见的嵌入维度来降低负样本评分,同时利用其余维度对正样本的有用信息进行编码。基于这些发现,我们即使在编码器提供的补丁表征中删减半数维度后,仍能保持与监督式图卷积网络相媲美的性能表现。
6. 核心代码
整个DGI网络的Pytorch实现为
class DGI(nn.Module):
def __init__(self, n_in, n_h, activation):
super(DGI, self).__init__()
self.gcn = GCN(n_in, n_h, activation)
self.read = AvgReadout()
self.sigm = nn.Sigmoid()
self.disc = Discriminator(n_h)
def forward(self, seq1, seq2, adj, sparse, msk, samp_bias1, samp_bias2):
h_1 = self.gcn(seq1, adj, sparse)
c = self.read(h_1, msk)
c = self.sigm(c)
h_2 = self.gcn(seq2, adj, sparse)
ret = self.disc(c, h_1, h_2, samp_bias1, samp_bias2)
return ret
# Detach the return variables
def embed(self, seq, adj, sparse, msk):
h_1 = self.gcn(seq, adj, sparse)
c = self.read(h_1, msk)
return h_1.detach(), c.detach()
7. 总结
核心是互信息,就是判断局部是否属于整体。从而在这套训练过程中找到最有价值的结构信息。



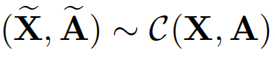

 浙公网安备 33010602011771号
浙公网安备 33010602011771号