论文解读-《Rethinking graph regularization for graph neural networks》

1. 论文介绍

论文题目：Rethinking graph regularization for graph neural networks
论文发表：AAAI 2021
论文领域：图神经网络
论文背景：

2. 论文摘要

图的拉普拉斯正则化项通常用于半监督表示学习，以提供模型的图结构信息。然而，随着近年来图神经网络（GNNs）的普及，直接将图结构编码到一个模型中已成为更为常见的方法。我们证明了图Laplacian正则化对现有GNN几乎没有益处，并提出了一种简单但非平凡的图Laplacian正则化变体，称为传播正则化（P-reg），以提高现有GNN模型的性能。通过形式化分析表明，P-reg不仅为GNN注入了传统的图Laplacian正则化无法捕捉到的额外信息，而且具有相当于无限深度图卷积网络的容量。我们证明了P-reg可以有效地提高现有GNN模型在节点级和图级任务上的性能。

3. 相关工作

传统的图拉普拉斯正则化能够提供的信息，目前的GNN也可以捕获图结构信息。

4. 本文算法-传播正则化Propagation-regularization

P-reg被定义为：

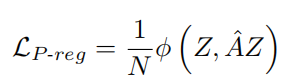
其中AZ是前向传播f的输出，φ函数衡量两者之间的差异，这里采用了典型的三种差异函数，如平方误差，交叉熵，Kullback–Leibler散度，这三者的计算公式为

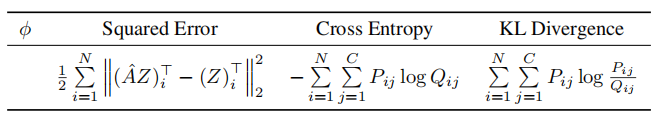
所以，整个GNN模型的损失函数可以被定义为

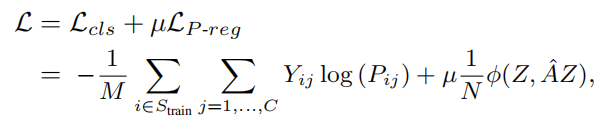
综上，整个p-reg的示意图

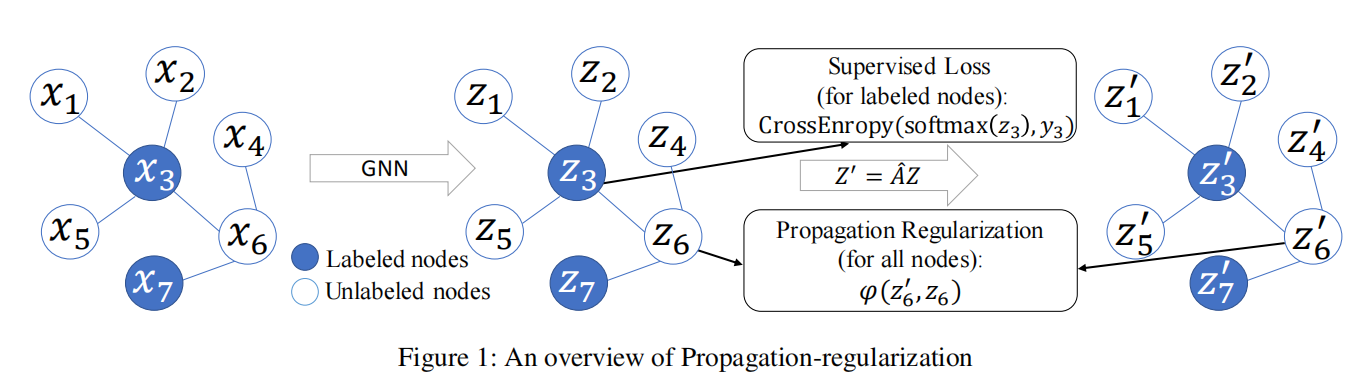
4.1 关于P-Reg如何和拉普拉斯正则化和深度图网络有联系

平方误差P-Reg与平方拉普拉斯正则化的等价性

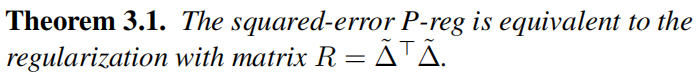
对于无限深的GCN，可以写为这样的表达式

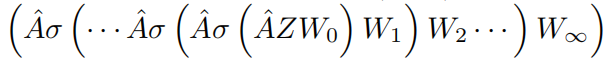
对于其中的激活函数为Relu，因为ReLU(·) = max(0, ·), 所以整个无限深GCN可以被简化为

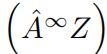
有引理：无限深的GCN可以让每一个节点捕获和提取到整个图的特征。

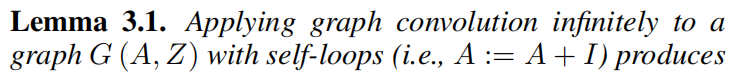
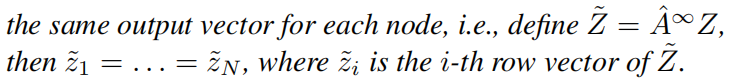
同时，让P-Reg最小化的同样也是需要一样的条件，这就让P-Reg最小化和无限深GCN联系上了

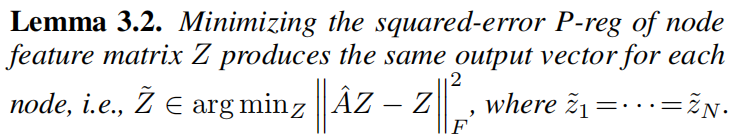
结合上面的两个引理，得到了相关联的结论。

4.2 P-Reg可以提高现有GNN方法的原因

从图正则化的角度，P-Reg可以提供额外信息给GNN以提高表现。
从无限深度GCN角度来说，P-Reg可以增强浅层GNN，以低消耗来实现深度GNN的模拟

4.2.1 P-Reg在图正则化方面的作用

1，图正则化项中提供了额外的监督信息。图正则化项作为一个非监督项，在使用到模型训练中，可以提供额外的监督学习的信息。这一点在半监督学习中，正则化项可以减少标签数据和非标签数据的群体距离。
2，图拉普拉斯正则化项目的局限性：目前GNN不能捕获的，正则化项也不能提供。
3，P-Reg如何解决图拉普拉斯正则化项的局限性，P-Reg提供了新的额外信息。
以节点为中心的P-Reg可以被视为使用了聚合了的邻域预测值作为每一个节点的监督目标，即AZ是Z的监督学习的目标，有了这个信号，准确率更高。

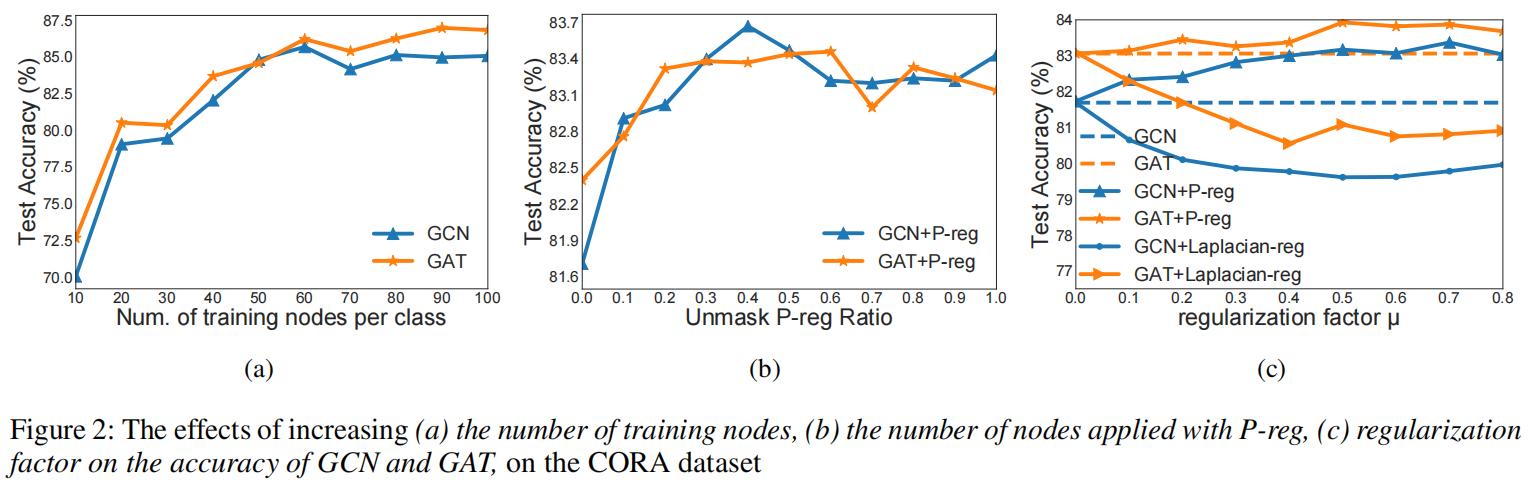
下图也说明了在P-Reg的限制上，不同标签的边界更加清晰

4.2.2 P-Reg在深度图卷积网络的作用

同样的，深度图卷积网路的是可以提供更远的节点的信息。K层网络相当于K跳的随机游走的邻居节点。
深度图卷积网络的局限性是层越深，节点产生的特征向量更易于相似。根据上面的引理，当层无限深的时候，所有的输出向量都是相同的，这个就是GNN的过平滑问题。相应的，深度越深，计算量越大。
P-Reg解决深度GCN的局限性：可以很好的在低消耗下很好平衡信息捕获和过度平滑问题，而且不需要考虑深度训练的梯度爆炸或消弭的问题。
实验验证效果为

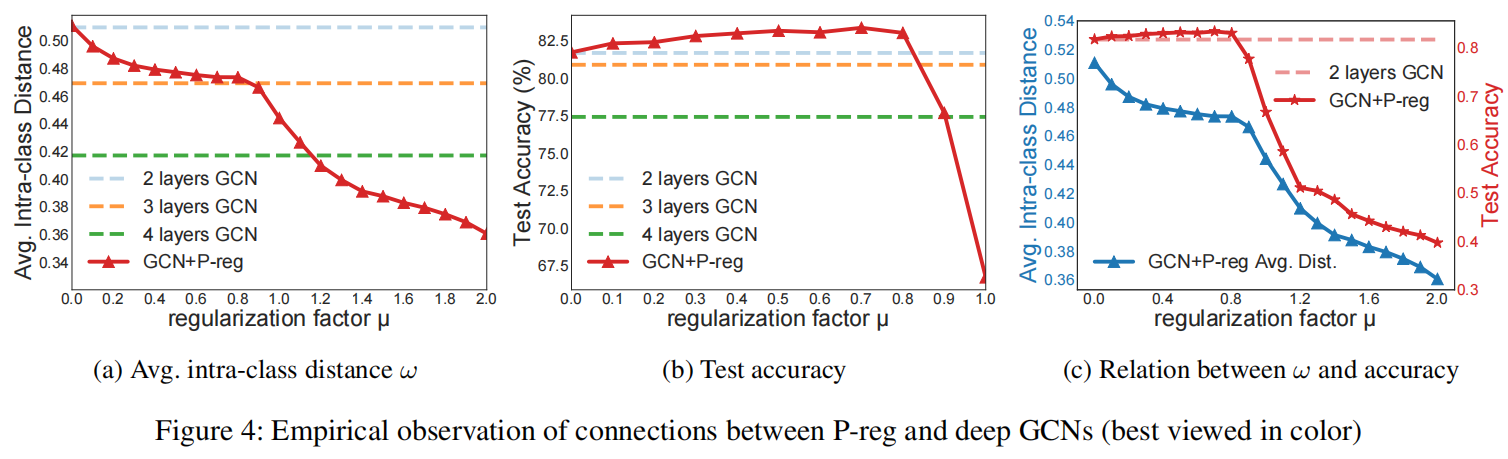
5. 实验设置

选择GCN，GAT，MLP作为基础模型，选择不同的正则化工具

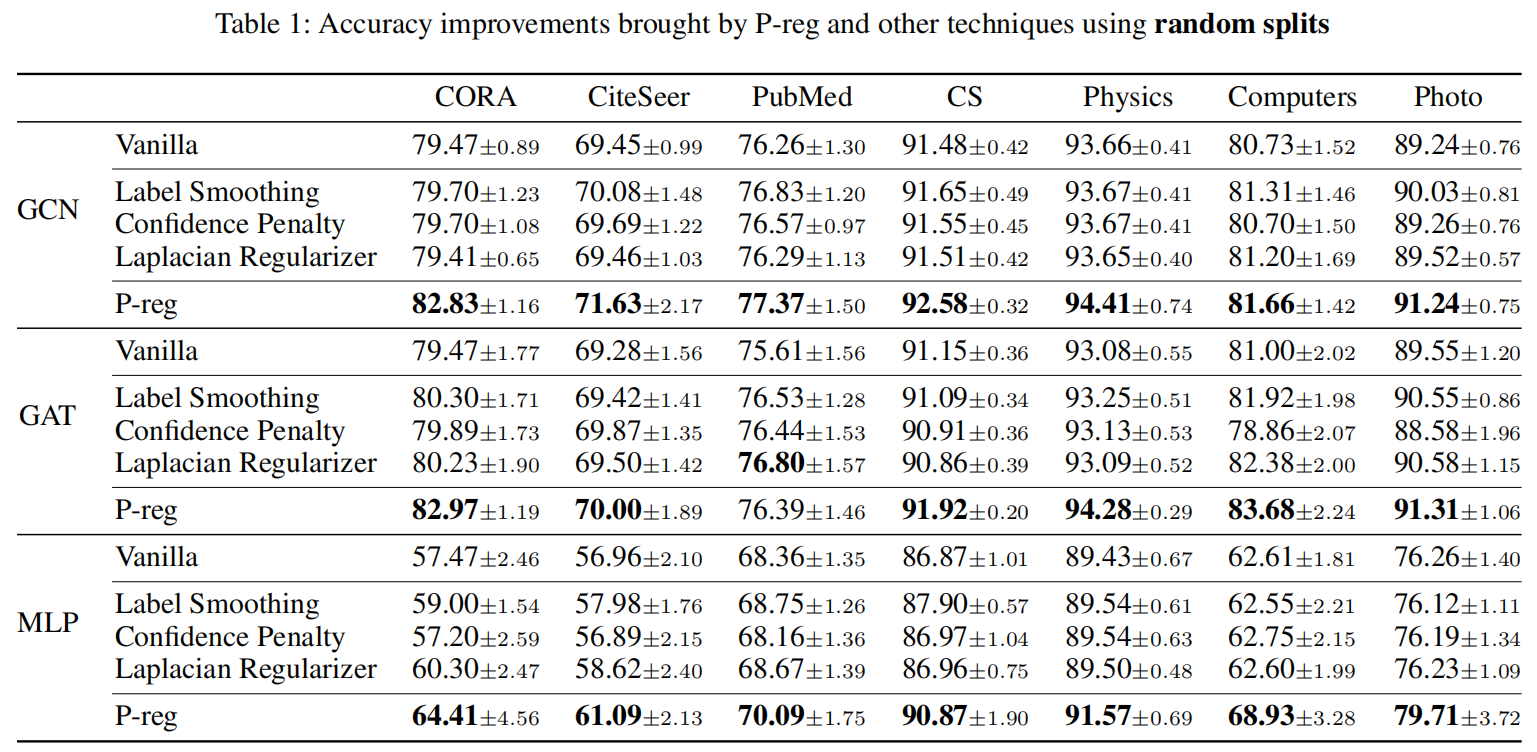
将P-Reg引入当前的GNN算法取得的效果提升

将P-Reg引入图级别任务的效果提升

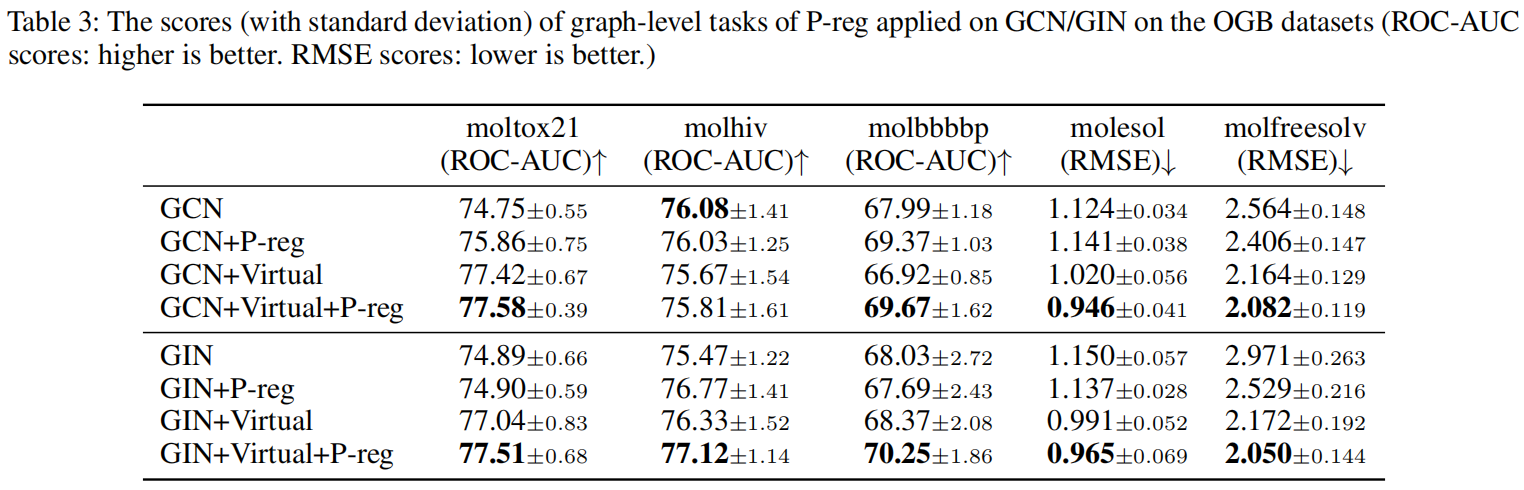
6. 总结

从一个训练的正则化项入手，研究相关的方法对比，和正则化项的数理证明。其中数学层面的剖析和研究值得学习。