论文解读-《signSGD: compressed optimisation for non-convex problems》

1. 论文介绍

论文名称：signSGD: compressed optimisation for non-convex problems
论文发表：ICML 2018
论文领域：分布式机器学习

2. 背景介绍

使用分布式架构来训练大型神经网络，其梯度通信消耗是一个大的瓶颈。本文的signSGD算法通过在只传递每次批量训练梯度的符号，就可以达到训练网络的效果。同时在梯度压缩和sgd级别的收敛速度上都取得了好的效果。

3. 本文算法

signSGD的核心算法，只是在传递的梯度上加入sign函数

还可以将本方法推广到动量SGD

推广到分布式训练中，使用sign后的最大投票数量

数值比较，本算法跟其他的SGD算法的数值比较

优化工作
大部分的经典优化问题聚焦在凸问题上，梯度的局部信息会告诉你全局最小点的方向。

很多基于sign的方法都取得了好的效果，如RPROP，还有其变形RMSPROP，和 ADAM。
adam使用了梯度的均值除以均方根来更新权值

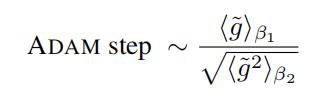
4. 理论分析框架

signSGD的收敛分析
设置了三个假设，来辅助在非凸环境下的收敛分析

• 1，最小边界假设：假设存在一个最小的f，使得所有x都符合f(x)>=f
• 2，平滑假设：通过限制梯度近似的误差，间接约束了Hessian矩阵的范围，让算法设计能够利用这种弱光滑性来分析收敛性
• 3，方差边界假设：随机梯度的期望等于真实梯度，同时控制方差有边界限制
  根据上面的假设，可以得到singnSGD的非凸收敛率

理论一，signSGD的非凸收敛率

理论二，多数投票下的分布式signSGD的非凸收敛率

对于信噪比S<1，会得到一个梯度很小的而不用担心sign问题，当S>1时，根据切比雪夫不等式，单个client上sign失效的概率小于0.5，那最后通过多数投票可以纠正解决。

5. 总结

文章通过给定一个理论分析框架来分析了sign函数对梯度下降的有效性。给出了边界假设，在假设下分析了梯度的几何边界面。
论文重在理论研究，整份证明理解不够，暂且搁笔，后期再深入研究。