论文解读-GCN

1，论文介绍

论文题目：Semi-Supervised Classification with Graph Convolutional Networks
论文发表

对于传统的半监督学习方法来说，图数据的损失函数：使用了基于图的拉普拉斯正则化项的。

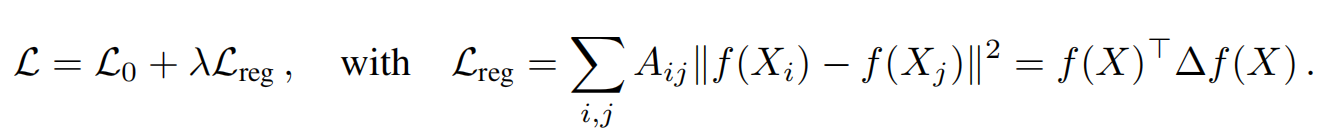
其中L0代表是是有监督损失， 后面的正则化项过于严格，要求节点之间的标签是平滑的，建立在相邻的节点有着类似的标签，这就限制了模型的表达能力，图的边不是必须连接类似节点，是由可能蕴含更多其他信息的。

2，论文贡献

1，提出了一种简单的，以层为单位的图神经网络
2，将这种图神经网络用于图的半监督学习，实验证明了取得了优秀效果

3，本文工作

图的快速近似卷积，基于切比雪夫网络的思想，使用切比雪夫一阶展开的卷积核，形成一层新的GCL，如果需要对多阶的特征进行提取，则进行多个GCL的堆叠即可实现。
图的特征可以被图上局部算子的一阶逼近来实现。

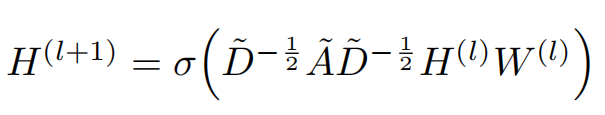
3.1，谱图卷积

谱图卷积可以定义为信号x和其核算子g在傅里叶域上的乘积。

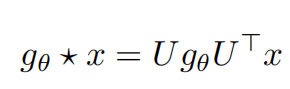
其中U是归一化图的拉普拉斯变换后的特征矩阵，计算量大。为了降低计算维度，使用切比雪夫多项式的K阶来近似g。

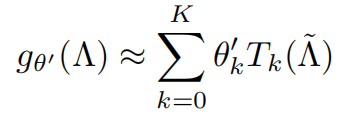
因为有：

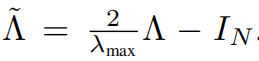
λmax代表的是L的最大特征值，

在多层级的网络里面，为了尽量简化的每一层的工作，把λmax近似为2，即可得到

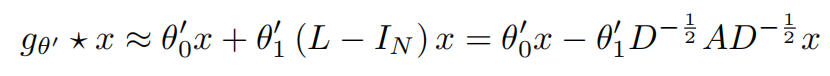
其中只有两个参数，而且这两个参数可以被整个图进行共享。
把上面的算子进行连续叠加即可达到提升一个节点的k阶近邻的特征。

在实际应用中，进一步限制参数的个数，减少两个为一个。
让

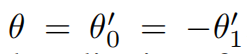
那么上面的公式变为

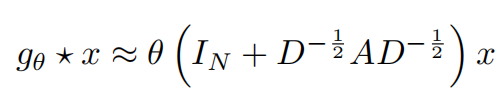
注意到 上面括号部分的表达式的范围为 [0, 2] ,那么多层的叠加可能会导致数值的不稳定。使用重新归一化技巧

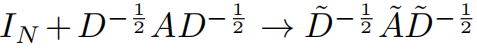
其中：


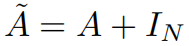
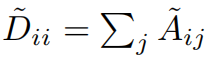
可以得到信号X的最终核算子

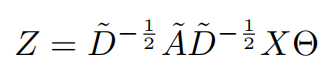
3.2实际应用

将上述的GCL来构建一个二层的GCN去解决半监督节点分类问题，基于一个对称邻接矩阵。
令

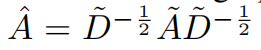
那么可以得到一个简单的形式

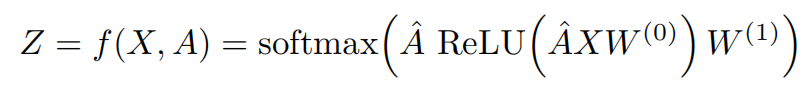
其中w0是第一层的可学习权重，w1是第二层的可学习权重。

网路示意图

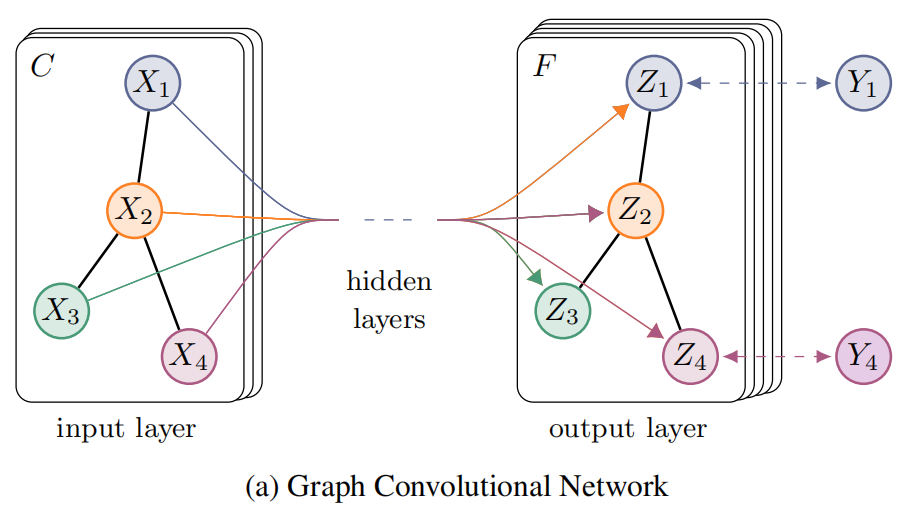
4，实验设置

半监督的节点分类实验，主要以planetoid为基础和主要对比对象

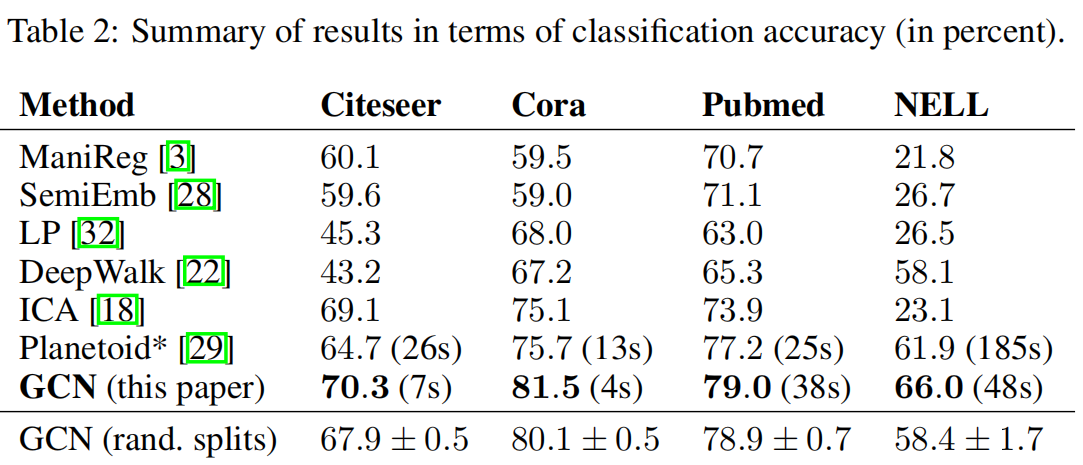
实验还针对不同的传播模型进行实验比较，实验也验证了本文的核心算法的效果。

5，代码实现

以下的代码为基于Pytorch来实现

# 图卷积层的定义
class GraphConvolution(nn.Module):
	def __init__(self, input_dim, output_dim, use_bias=True):
		super(GraphConvolution, self).__init__()
		self.input_dim = input_dim						# 输入特征向量的维度
		self.output_dim = output_dim					# 输出特征向量的维度
		self.use_bias = use_bias
		self.weights = nn.Parameter(torch.Tensor(input_dim, output_dim))
		if self.use_bias:
			self.bias = nn.Parameter(torch.Tensor(output_dim))
		else:
			self.register_parameter('bias', None)
		self.reset_parameters()

	def reset_parameters(self):
		init.kaiming_uniform_(self.weights)
		if self.use_bias:
			init.zeros_(self.bias)

	def forward(self, adjacency, input_feature):
		support = torch.mm(input_feature, self.weights)
		output = torch.sparse.mm(adjacency, support)
		if self.use_bias:
			output += self.bias
		return output

	def __repr__(self):
		return self.__class__.__name__ + '(' + str(self.input_dim) + \
			' -> ' + str(self.output_dim) + ')'

# 二层的图卷积神经网络
class GCNNet(nn.Module):
	def __init__(self, input_dim=1433, hiddden_dim=16, output_dim=7):
		super(GCNNet, self).__init__()
		self.gcn1 = GraphConvolution(input_dim, hiddden_dim)
		self.gcn2 = GraphConvolution(hiddden_dim, output_dim)

	def forward(self, adjacency, feature):
		h = F.relu(self.gcn1(adjacency, feature))
		h = F.dropout(h, p=0.5, training=self.training)
		logits = self.gcn2(adjacency, h)
		return logits

6，总结

算法的理论是一脉相承下来。一般关键点的论文，对前人工作的分解，简化和优化，一般能做到简化和提效，基本可以意味着一种新的通用方法的可广泛推广。