【学习笔记】反射容斥 & 推广
声明:本文为博主「zhang_kevin」的原创文章,遵循CC 4.0 BY-NC-SA版权协议,您转载时请于明显处附上原文链接及本声明,而且您不得为商业目的而使用本作品。
原文链接:https://www.cnblogs.com/zhang-kevin/articles/19243539。
本文同步发表于洛谷博客。
我在某天听杂题选讲的时候,遇到了反射容斥。当时不会,所以去补了,然后就有了这篇文章。
正文开始~
一、前置芝士
在深入学习反射容斥之前,先回顾一下格路模型和容斥原理。
1. 格路模型
-
定义:在一个平面直角坐标系中,从一个点 \(P(x_1, y_1)\) 到另一个点 \(Q(x_2, y_2)\) 的格路指仅通过向右走(\(x + 1\))或向上走(\(y + 1\)),到达终点的一条路径。其中,坐标都是整数,而且满足 \(x_2 \geq x_1\),\(y_2 \geq y_1\)。
-
格路计数:从一个点 \(P(0, 0)\) 走到另一个点 \(Q(n, m)\) 的格路总数为 \(C_{n + m}^n\)。
原因:从 \(P\) 走到 \(Q\) 共需要走 \(n + m\) 步,我们任选 \(n\) 步往右,其余步数往上即可。因此,总方案数为 \(C_{n + m}^n\)。
2. 容斥原理
思考:我们想求出满足限制 \(p\) 或限制 \(q\) 的情况数,但直接做很难,怎么办呢?
回答:利用容斥原理。具体地,满足 \(p\) 的情况数,加上满足 \(q\) 的情况数,减去同时满足 \(p\) 和 \(q\) 的情况数,就是答案。有时候,利用容斥原理转化一下会更容易做。
当然,上面提到的是最简单的容斥。这里给出容斥原理的通用公式:
严谨证明略,可以画个韦恩图感性理解简单情况。
二、核心思想
现在介绍反射容斥的核心思想。个人认为,反射容斥更像一种思想,而不是算法。
1. 核心问题
思考下面这个问题:
给定起点 \(P(0,0)\) 和终点 \(Q(n,n)\),求有多少条格路满足不跨过直线 \(y = x\)(即任意时刻满足 \(y \leq x\))?
如果没有限制,根据刚才的格路模型,答案是 \(C_{2n}^n\)。
但现在有限制,因此需要减去不合法的方案数。
现在,问题变成了如何求出不合法的方案数。
我们先给出结论:
不合法的方案数等于从 \((0,0)\) 到 \((n - 1, n + 1)\) 的格路数量。
证明:
首先,我们可以把「不跨过直线 \(y = x\)」转化成「不触碰直线 \(y = x + 1\)」。
设所有不合法的格路组成的集合是 \(A\),所有从 \((0, 0)\) 走到 \((n - 1, n + 1)\) 的格路组成的集合是 \(B\)。
考虑这样一个法则 \(f\):对于一条 \(A\) 中的格路,它第一次碰到直线 \(y = x + 1\),一定是从某点 \((k, k)\) 走到 \((k, k + 1)\) 造成的。我们把这条格路在点 \((k, k + 1)\) 之后的部分全部关于直线 \(y = x + 1\) 翻折,得到新的格路。
显然,根据法则 \(f\) 可以得到从 \(A\) 到 \(B\) 的映射。注意这是一个合法的映射,因为点 \((n, n)\) 关于直线 \(y = x + 1\) 翻折后得到的是 \((n - 1, n + 1)\)。
下面,我们证明这个映射是一个双射。
一方面,这个映射是单射。因为两条不同的非法格路如果反射后得到了同一条格路,则得到的格路最先碰到直线 \(y = x + 1\) 的点一定同时是两条非法格路第一个碰到 \(y = x + 1\) 的点。这导致了两条格路前面一部分相同。同样,后边部分翻转后相同,则翻转前也想通!这样我们推出了两条格路相同,与前提矛盾。故这是单射。
另一方面,这个映射是满射。考虑任取 \(B\) 集合中的一条格路,我们需要证明 \(A\) 中存在一条格路可以映射到它。显然,\(B\) 中选择的格路从 \((0,0)\) 到 \((n - 1, n + 1)\),其一定会穿过 \(y = x + 1\),故存在第一个碰到 \(y = x + 1\) 的点。此时,把格路后半部分关于 \(y = x + 1\) 翻转,就会得到一条 \(A\) 中的格路,显然这条格路可以映射到 \(B\) 中选择的格路!故这也是满射。
由于该映射既是单射也是满射,因此它是一个双射。
既然证明了是双射,显然有 \(|A| = |B|\),故得到了不合法的方案数等于从 \((0,0)\) 到 \((n - 1, n + 1)\) 的格路数量。
证毕。
现在我们证明了结论,这个问题也就解决了。从 \((0,0)\) 到 \((n - 1, n + 1)\) 的格路数量是 \(C_{2n}^{n - 1}\),故原问题的答案是 \(C_{2n}^n - C_{2n}^{n - 1}\)。
P.S. 我们证明了 Catalan 数的一个公式。
2. 思想推广
反射容斥的思想不仅可以用于 \(y = x\),还可以用于任意其他斜率为 \(1\) 的直线(或水平、垂直的直线),解决思路与刚才一致。
这里主要想介绍的,是双线反射容斥。
考虑一下,如果有两条平行的直线,要求格路始终在两条直线之间,怎么办呢?
先看一个例题:
给定起点 \(P(0,0)\) 和终点 \(Q(n,m)\),求有多少条格路满足不跨过直线 \(y = x + 1\),也不跨过直线 \(y = x - 1\)?
这个问题需要结合容斥原理解决。
具体地,对于终点 \(Q\),假设其关于两条直线翻折后得到的点是 \(a\) 和 \(b\),再假设 \(a\) 和 \(b\) 关于两条直线翻折后得到的非 \(Q\) 的点是 \(a'\) 和 \(b'\),再得到 \(a''\) 和 \(b''\),等等。则我们有结论:格路数量等于 \(f(Q) - (f(a) + f(b)) + (f(a') + f(b')) - (f(a'') + f(b'')) + (f(a''') + f(b''')) \cdots\),其中 \(f(x)\) 表示从 \((0, 0)\) 到点 \(x\) 的格路数量。
理论上我们需要无限翻折计算。但注意到,当某次计算时 \(f = 0\),则以后的计算都没意义了,可以停止。
这样做的时间复杂度是 \(\mathcal{O}(\frac{n + m}{d})\),其中 \(d\) 是两条直线的距离。
三、例题
学完了,就写题吧。
4th Ucup S3 E - Maximum Segment Sum
我本来不想放这道题的,但由于这道题导致了这篇文章,所以还是放了,纪念一下这道题。
初学建议先跳过这道题,去看看习题。
题目链接:https://qoj.ac/problem/14419。
题意简述
给定序列长度 \(n\),序列的每一项可以是 \(1\) 或 \(-1\)。
对于每一个 \(k\),求出有多少序列满足最大子段和为 \(k\)。
答案对 \(998244353\) 取模。
数据范围:\(1 \leq n \leq 5 \times 10^5\);\(1.5s\)、\(1024MB\)。
题解
首先考虑对于给定序列,如何求其最大子段和。
显然,我们可以维护一个变量 \(cur\),每次执行 \(cur \leftarrow \max(0, cur + a_i)\),并记录整个过程中最大的 \(cur\) 即可。
其次,我们可以通过容斥原理,把恰好为 \(k\) 转化为不超过 \(k\)。
我们用一个平面直角坐标系去刻画 \(cur\) 的变化,可以得到如下所示的图:
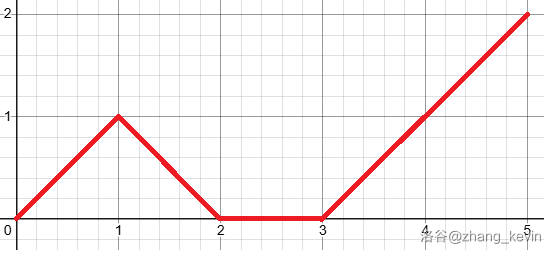
显然,不超过 \(k\) 就是不能跨过 \(y = k\),即不能碰到 \(y = k + 1\)。
但跟 \(0\) 取 \(\max\) 这个操作很烦,故考虑把它变成碰到 \(y = -0.5\) 就反射。显然,如果我们这样反射但不容斥,可以解决跟 \(0\) 取 \(\max\) 的问题。
但是,翻转后也得保证不超过 \(k\),因此我们需要同时满足不碰到 \(y = k + 1\) 和 \(y = -k - 2\)。
此时问题已经变成很标准的双线反射容斥了。但注意,你的终点实际上是很多点,不能直接计算。
容易发现终点们组成了一条垂线段,垂线段关于某条水平直线翻折仍然是垂线段!因此,利用前缀和统计组合数的和即可。
P.S. 学到了一种神奇的语法,可以直接处理偏移量,详见代码。
参考代码(C++):
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x = 0, f = 1;
char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)){
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
inline void write(int x){
if(x < 0) putchar('-'), x = -x;
if(x > 9) write(x / 10);
putchar(x % 10 + '0');
return;
}
const int Mod = 998244353;
int n, fac[4100000], inv[4100000];
int Pre[4100000], *pre = Pre + 2000000;
int Ans[4100000], *ans = Ans + 2000000;
inline int fp(int a, int b){
int res = 1;
while(b){
if(b & 1) res = res * a % Mod;
a = a * a % Mod;
b >>= 1;
}
return res;
}
inline int sum(int l, int r){return (pre[r] - pre[l - 1] + Mod) % Mod;}
signed main(){
//Input
n = read();
//Init
const int N = 4000000;
fac[0] = 1; for(int i = 1; i <= N; i++) fac[i] = fac[i - 1] * i % Mod;
inv[N] = fp(fac[N], Mod - 2); for(int i = N; i >= 1; i--) inv[i - 1] = inv[i] * i % Mod;
for(int i = -n; i <= 3 * n; i++){
pre[i] = (pre[i - 1] +
(
abs(n - i) & 1 ? 0 : fac[n] * inv[(n + i) >> 1] % Mod * inv[(n - i) >> 1] % Mod
)
) % Mod;
}
//Solve
for(int k = 0; k <= n; k++){
for(int x = ((k + 1) - (-k - 2)), f = -1; x - k - 1 <= n; x += ((k + 1) - (-k - 2))) ans[k] = (ans[k] + f * sum(x - k - 1, x + k)) % Mod, f = -f;
for(int x = 0, f = 1; x + k >= -n; x -= ((k + 1) - (-k - 2))) ans[k] = (ans[k] + f * sum(x - k - 1, x + k)) % Mod, f = -f;
}
for(int k = n; k >= 1; k--) ans[k] = (ans[k] - ans[k - 1] + Mod) % Mod;
//Output
for(int k = 0; k <= n; k++) write((ans[k] % Mod + Mod) % Mod), putchar(" \n"[k == n]);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号