浅谈二分图
声明:本文为博主「zhang_kevin」的原创文章,遵循CC 4.0 BY-NC-SA版权协议,您转载时请于明显处附上原文链接及本声明,而且您不得为商业目的而使用本作品。
原文链接: https://www.cnblogs.com/zhang-kevin/articles/18931608
正文开始~
前言
-
这篇文章改编自我曾经做的二分图课件,所以文字可能比较奇怪,请谅解;
-
文章中提供一些例题,建议先独立思考再看题解(题解不提供代码);
\(\texttt{Part 1}\):二分图基本知识
我们先学习一些二分图相关的基本知识。
二分图的定义
二分图,又称二部图,他的节点由两个集合组成,且两个集合内部没有边。
换句话说,一个图是二分图,要求存在一种方案,可以将节点划分成满足以上性质的两个集合。
例如,这是二分图:
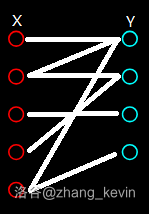
二分图的性质
- 如果两个集合中的点分别染成红色和蓝色,可以发现二分图中的每一条边都一定是连接一个红色点和一个蓝色点。

- 二分图不存在长度为奇数的环(因为每次都是从一个集合走到另一个集合,所以必须走偶数次才能回到出发的集合)。
二分图的判定
这里有一个很重要的判定定理:
一个图是二分图当且仅当它不包含奇数长度的环
在使用代码判断的时候,我们考虑染色法。
对图进行一次 dfs,第一个点染成红色,与之相邻的染成蓝色。
然后对于蓝色点相邻的所有点染成红色。
重复上述过程。
如果发现一个点即将要染的颜色与原来的颜色不同,说明这个图不是二分图。
反之这个图是二分图,染色结果就是构造。
例题 \(\texttt{1}\)
有 \(n\) 个罪犯和三个序列 \(a,b,c\),其中 \(a_i\) 与 \(b_i\) 两名罪犯之间有 \(c_i\) 大小的冲突。现要将这些罪犯分配到两个监狱中,只有在同一个监狱时两名罪犯才会发生冲突。求能分配的最小的冲突最大值。
特别的,你不知道什么是并查集。
题解
这就是经典的关押罪犯,我们考虑不使用并查集来解决。
显然可以二分答案。具体来说,将所有罪犯的冲突 \(c\) 按照影响力从大到小排序,二分答案时的 mid 表示冲突数组中的第几个(可以理解为二分下标)。
我们将比 \(c_{mid}\) 大的冲突关系都连边。显然此时只要这个图是二分图,答案就合法。因此 check 函数判断该图是否是二分图即可,判断方法就是染色法。
\(\texttt{Part 2}\):二分图最大匹配相关知识
下面我们学习二分图最大匹配相关知识。
前言
这是一个在 OI 界中几乎不会以单质(所以是化合物?)存在的东西。
但二分图最大匹配常结合一些复杂的建模,以及一些其他算法。
所以,还是有必要学习的。
另外很多建模用的 trick 也需要通过刷题得到。
二分图最大匹配定义
匹配的定义
-
定义:图 \(G\) 的一个匹配是 \(G\) 的一个边集 \(E\),满足 \(E\) 中的所有边都没有公共端点。
-
说人话就是一张图的一个匹配是一堆没有公共端点的边。
最大匹配的定义
- 显然就是边数最多的匹配。
注意这不是二分图最大权匹配。
匈牙利算法
匈牙利算法是常用的二分图匹配算法,其正确性基于 Hall 定理。
算法的时间复杂度为 \(\mathcal{O}(n \times e + m)\),\(n\) 是左部点个数,\(e\) 是图的边数,\(m\) 是右部点个数。显然有一个小 trick 就是可以交换左右部,使得左部点更少,从而提升效率。
我们先通过图示简单理解一下算法过程(图完全手绘,不好看请谅解……)。
下图是一个普通的二分图。
我们称呼左边的点为红 \(1\)、红 \(2\)、红 \(3\)、红 \(4\),称呼右边的点为蓝 \(1\)、蓝 \(2\)、蓝 \(3\)、蓝 \(4\)。
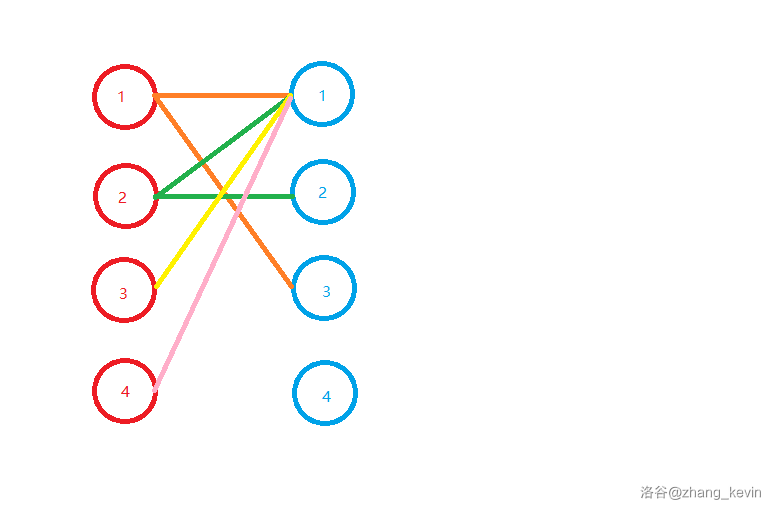
我们先取第一条边(\(\text{红} 1 \rightarrow \text{蓝} 1\)),当做匹配边(黑色表示)。
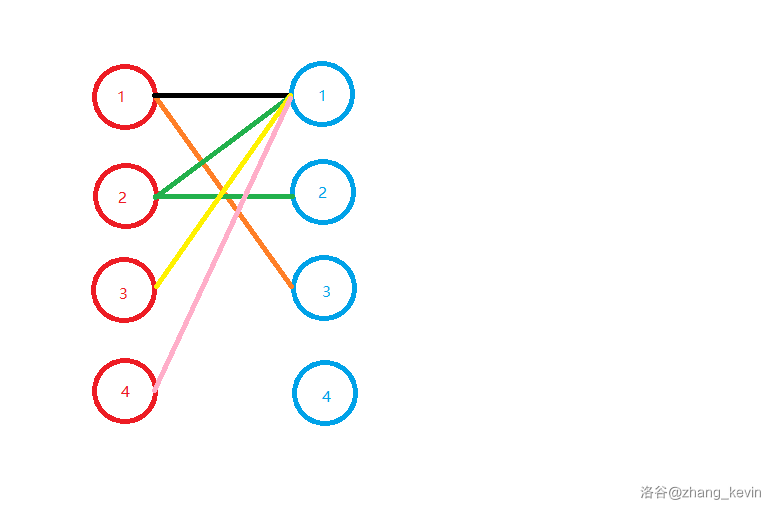
现在红 \(1\) 已经被匹配了,所以考虑红 \(2\)。我们把红 \(2\) 的第一条边当做匹配边。
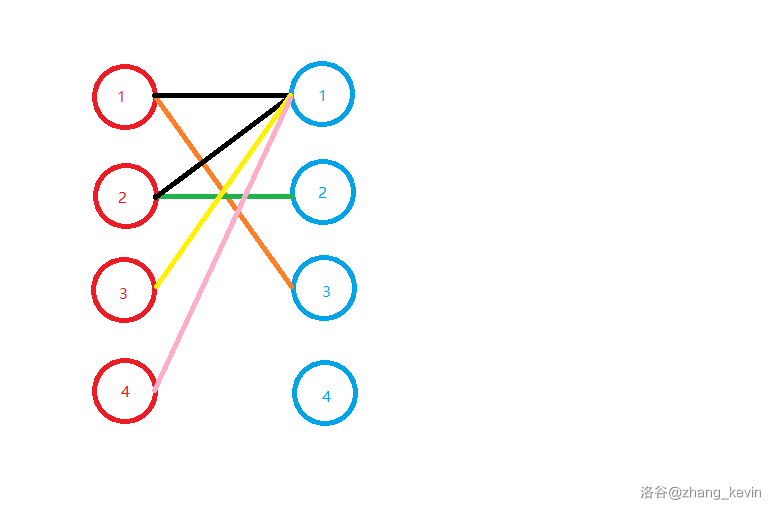
这个时候,我们发现,蓝 \(1\) 被匹配了两次!
于是,我们让蓝 \(1\) 的原配尝试找别人。
显然,他的原配红 \(1\) 能找到蓝 \(3\),所以让红 \(1\) 去匹配蓝 \(3\)。
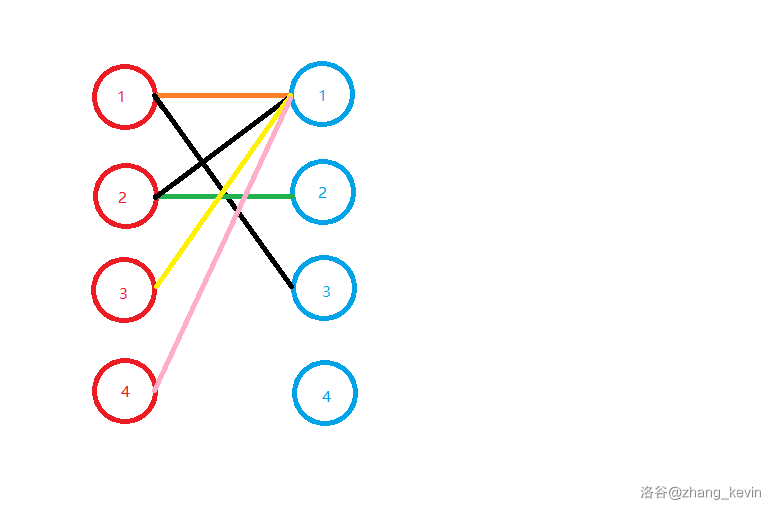
现在考虑红 \(3\),同理把红 \(3\) 的第一条边当做匹配边。
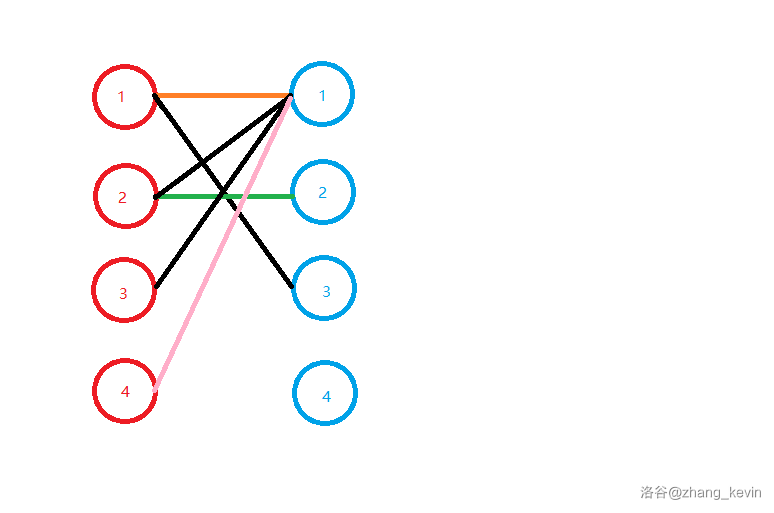
然后,蓝 \(1\) 又被匹配了两次!
于是,我们再次让蓝 \(1\) 的原配尝试找别人。
他的原配红 \(2\) 能找到蓝 \(2\),所以让红 \(2\) 去匹配蓝 \(2\)。
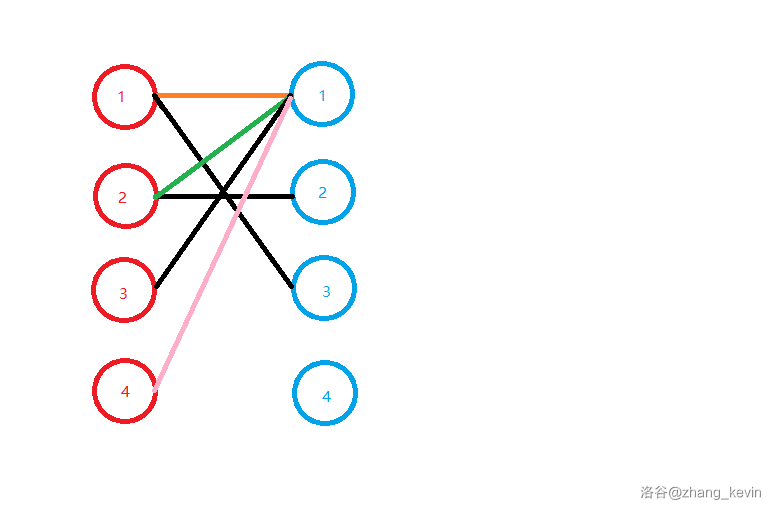
最后考虑红 \(4\),同理把红 \(4\) 的第一条边当做匹配边。
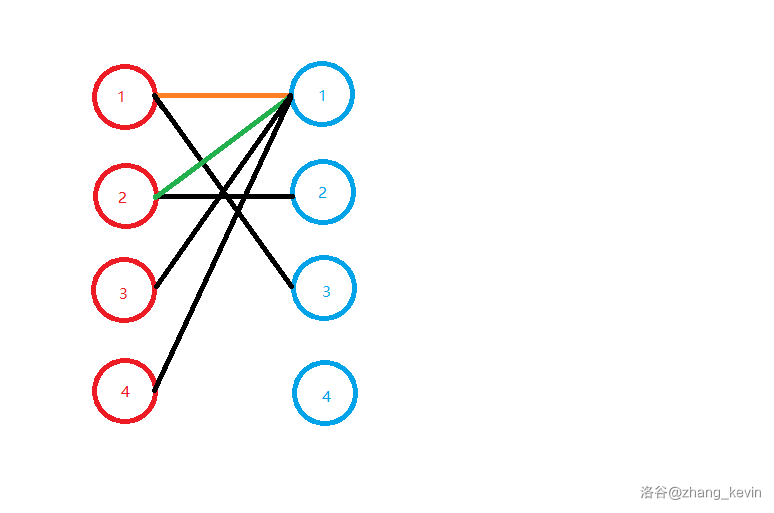
现在,蓝 \(1\) 叕被匹配了两次!
于是,我们再次让蓝 \(1\) 的原配尝试找别人。
但他的原配红 \(3\) 找不到别人了。
于是红 \(4\) 失配,他的第一条边不再是匹配边。
又因为他没有第二条边了,所以算法结束。

最终得到结论:最大匹配等于 \(3\)。
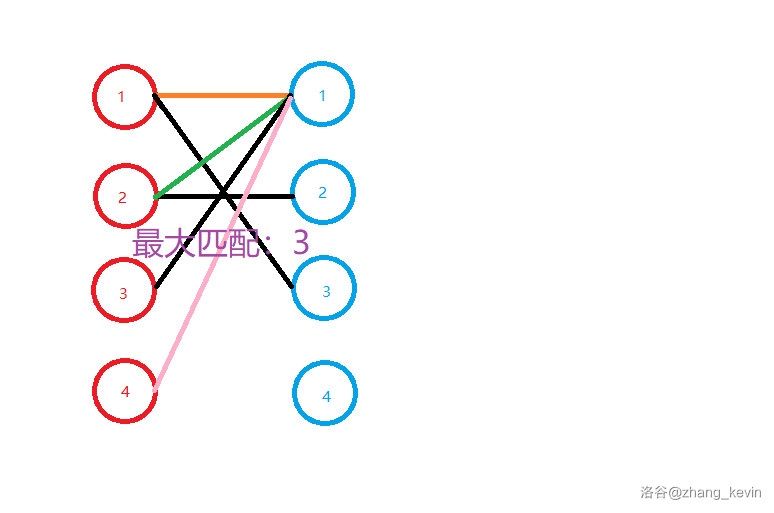
算法过程的文字描述:枚举每一个左部点 \(u\),然后枚举该左部点连出的边,对于一个出点 \(v\),如果它没有被先前的左部点匹配,那么直接将 \(u\) 匹配 \(v\),否则尝试让 \(v\) 的“原配” 左部点去匹配其他右部点,如果“原配” 匹配到了其他点,那么将 \(u\) 匹配 \(v\),否则 \(u\) 失配。
参考代码:
bool dfs(int u){
for(int i = head[u], v; i; i = nxt[i]){
if(!vis[v=to[i]]){
vis[v] = 1;
if(!match[v] || dfs(match[v])){
match[v] = u; return true;
}
}
}
return false;
}
void solve(){
for(int i = 1; i <= leftn; i++){
memset(vis, 0, sizeof(vis));
if(dfs(i)) ans++;
}
}
特别的,这个算法需要以增广路的思想去理解,因为后面的学习需要用到。
网络流求二分图最大匹配
这里不详细介绍网络流了,算法过程就是建立一个源点和一个汇点,然后跑一遍 Dinic。
Hall 定理
下面讲一下 Hall 定理。
定理内容:
对于一个二分图 \(G\),假设 \(G\) 的两个集合分别为 \(X\)、\(Y\),且 \(X\) 小一些,有 \(n\) 个点;则 \(G\) 存在完美匹配的充分必要条件是对于任意一个 \(X\) 的子集,设大小为 \(k\),那么和这个子集相连的 \(Y\) 必须不小于 \(k\) 个。
必要性证明:
假设一个二分图 \(G\) 存在完美匹配,且不满足 Hall 定理。
那么一定存在 \(k\) 个点,它们一共连向的点都不足 \(k\) 个。
那么,请问你们都是怎么被匹配上的?
因此必要性正确。
充分性证明:
假设一个二分图 \(G\) 不存在完美匹配,且满足 Hall 定理。
设其最大匹配为 \(M\),其对应的点集为 \(X,Y(|X| \leq |Y|)\)。
则一定可以从某个点 \(v_i \notin X\) 出发,由于满足 Hall 定理,这条路一定能够遍历 \(Y\) 中的 \(|X|+1\) 个点,即我们找到了一条增广路。这与 \(M\) 是最大匹配的假设矛盾。故得证。
因此充分性正确。
推论
Hall 定理推论:
二分图 \(G\) 的最大匹配为 \(|X| - \max (|X'|-|N(X')|)\),其中 \(X\) 是数量较少的集合,\(X'\) 是 \(X\) 的任意子集,\(N(u)\) 表示 \(u\) 的邻居节点集合。
例题 \(\texttt{2}\)
一共有 \(n\) 个飞行员,其中有 \(m\) 个外籍飞行员和 \((n - m)\) 个英国飞行员,外籍飞行员从 \(1\) 到 \(m\) 编号,英国飞行员从 \(m + 1\) 到 \(n\) 编号。 对于给定的外籍飞行员与英国飞行员的配合情况,试设计一个算法找出最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
本题存在 Special Judge。
对于 \(100\%\) 的数据,保证 \(1 \leq m \leq n < 100\),\(1 \leq u \leq m < v \leq n\),同一组配对关系只会给出一次。
题解
题目:https://www.luogu.com.cn/problem/P2756。
显然建二分图。
如果你使用匈牙利算法,那么恭喜你,你的算法自带匹配方案。
如果你使用网络流,只需要在求出答案后,判断边是否有流量即可。
例题 \(\texttt{3}\)
给出一张 \(n \times n(n \leq 100)\) 的国际象棋棋盘,其中被删除了一些点,问可以使用多少 \(1 \times 2\) 的多米诺骨牌进行掩盖。
题解
考虑黑白交替染色,这样每一块骨牌需要覆盖一黑一白。
白色当成左部点,黑色是右部点,相邻则连边。
显然求出最大匹配就好了。
例题 \(\texttt{4}\)
给定一个 \(N\) 行 \(M\) 列的棋盘,已知某些格子禁止放置。
问棋盘上最多能放多少个不能互相攻击的車。
車放在格子里,攻击范围与中国象棋的“車” 一致。
数据范围:\(1 \le N,M \le 200\)。
题解
题目:https://www.luogu.com.cn/problem/P10937。
考虑每一行当成左部点,每一列当成右部点,如果行列相交就连边。
这样一个边被选中,代表放置一个車,而且要求其他边与之没交点。
显然这就是最大匹配,于是跑一遍匈牙利或网络流就好了。
例题 \(\texttt{5}\)
城堡有 \(m\) 个敌人、\(n\) 个能发射导弹的防御塔。导弹的速度固定,都为 \(v\)。导弹需要 \(T_1\) 秒发射,\(T_2\) 分钟冷却,还需要防御塔到敌人距离的 \(\frac{dis}{v}\) 的时间,导弹遇到目标后立即将其摧毁。给定防御塔和敌人的坐标,求需要多少分钟能够消灭所有敌人。
数据范围:\(1 \le N,M \le 50\),坐标绝对值不超过 \(10000\),\(T_1,T_2,V\) 为不超过 \(2000\) 的正整数。
题解
题目:https://www.luogu.com.cn/problem/P10936。
显然答案具有单调性,所以考虑二分答案。题目变为 \(mid\) 时间内能不能消灭敌人。
考虑建二分图,左边是防御塔,右边是敌人。
显然我们可以计算出 \(mid\) 时间内最多发射多少导弹,假设为 \(P\)。
因此我们把一个防御塔拆成 \(P\) 个有序导弹。如果导弹可以在 \(mid\) 时间内到达敌人,就连一条边。
最后判断最大匹配是不是敌人个数就好了。
特别的,二分图中的点可以被匹配多次(但仍有上限)前提下的最大匹配问题,称为二分图的多重匹配问题。拆点是经典的解决方法,网络流也不错。
补充知识
补充知识:二分图最小点覆盖、二分图最大独立集。
二分图最小点覆盖
最小点覆盖:选最少的点,满足每条边至少有一个端点被选。
König 定理:二分图中,最小点覆盖包含的点数等于最大匹配包含的边数。
证明如下:
显然二分图最大匹配是原图的一个子集,而且所有边不相交。
所以,选择最小点覆盖的时候至少要每条边选一个。
也就是:最小点覆盖包含的点数大于等于最大匹配包含的边数。
所以,我们只需要给出一种构造,使得点覆盖数量等于最大匹配包含的边数即可。
考虑如下构造:
从左侧未匹配的节点出发,按照匈牙利算法中增广路的方式走,即先走一条未匹配边,再走一条匹配边。
由于已经求出了最大匹配,所以这样的增广路一定是不完整的(以匹配边结束)。
在所有经过这样「增广路」的节点上打标记。则最后构造的集合是:所有左侧未打标记的节点和所有右侧打了标记的节点。
下证这个集合的大小等于最大匹配以及这个集合是一个点覆盖。
首先,这个集合的大小等于最大匹配。考虑这些事情:
-
左部非匹配点一定被标记:因为你们是出发点;
-
右部非匹配点一定没有被标记:否则你的匈牙利就出 Bug 了(有增广路);
-
每对匹配点要么都被标记,要么都没被标记:因为左部匹配点只能通过右部到达。
我们的选择是:所有左侧未打标记的节点和所有右侧打了标记的节点。
因此,一定正好对每条匹配边选择了一个点。
故选出的点数正好等于二分图的最大匹配数。
二分图最大独立集
最大独立集:选最多的点,满足两两之间没有边相连。
因为在最小点覆盖中,任意一条边都被至少选了一个顶点,所以对于其点集的补集,任意一条边都被至多选了一个顶点,所以不存在边连接两个点集中的点,且该点集最大。因此二分图中,最大独立集 \(=n-\) 最小点覆盖。
例题 \(\texttt{6}\)
在一个 \(n \times n\) 个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍,骑士不得进入。
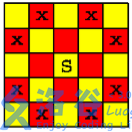
对于给定的 \(n \times n\) 个方格的国际象棋棋盘和障碍标志,计算棋盘上最多可以放置多少个骑士,使得它们彼此互不攻击。
\(1 \leq n \leq 200\),\(0 \leq m \lt n^2\)。
题解
题目:https://www.luogu.com.cn/problem/P3355。
考虑如题目中的图进行染色,我们发现同色格子不能互相攻击。
因此,把黄色的看做一个集合,红色的看做另一个集合。然后把可以互相攻击的格子连边(排除不能放的位置)。
此时形成了一个二分图,而我们求的是二分图的最大独立集。
所以输出「\(n^2 - m\) \(-\) 最大匹配」即可。
例题 \(\texttt{7}\)
如图所示,西洋棋的“长脖子鹿”,类似于中国象棋的马,但按照“目” 字攻击,且没有中国象棋“别马腿” 的规则。(因为长脖子鹿没有马腿)
给定一个 \(N \times M\) 的棋盘,有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。
\(1 \leq N,M \leq 200\)。
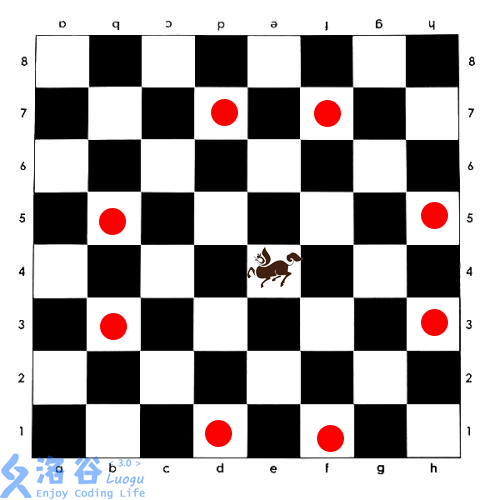
题解
题目:https://www.luogu.com.cn/problem/P5030。
考虑条形染色。
然后就跟例题 \(\texttt{6}\) 一样了。
例题 \(\texttt{8}\)
在一块 \(N \times M\) 的网格状地面上,有一些格子是泥泞的,其他格子是干净的草地。现在需要用一些宽度为 \(1\)、长度任意的木板把泥地盖住,同时不能盖住干净的地面。每块木板必须覆盖若干个完整的格子,木板可以重叠。求最少需要多少块木板。
保证:\(1 \leq N,M \leq 50\)。
题解
题目:https://www.luogu.com.cn/problem/P6062。
以样例为例:

黄色是泥地,绿色是草地。
考虑这两块木板:
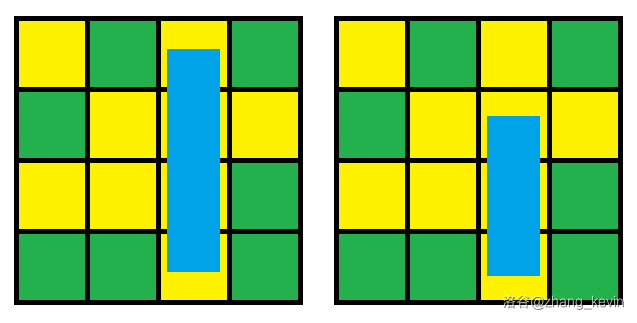
显然左边更优。
于是,枚举所有木板可能的放置位置:
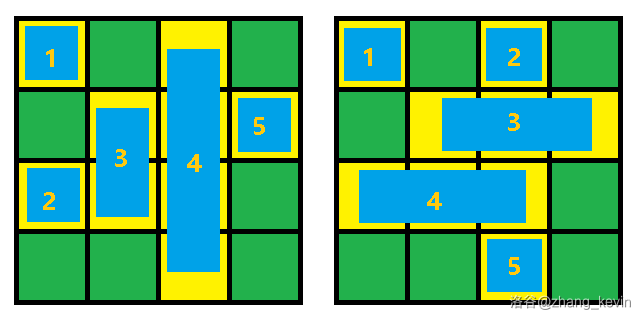
一个格子要么被横着的木板覆盖,要么被竖着的格子覆盖。
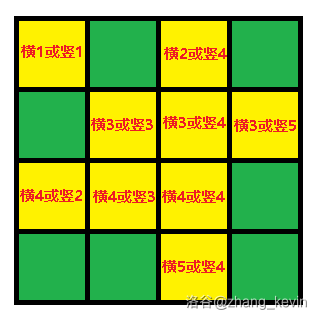
所以写出每个格子被覆盖需要选择哪两块木板。
我们把横着的看做左部点,竖着的看做右部点。
如果两块板子同时满足一个格子的需求,就把这两个板子连边。
显然,选择一个点就是放置一块木板,而 与这个点所连的所有边 所对应的格子 都可以被这块木板覆盖。
于是我们求一下最小点覆盖就可以了。
由 König 定理得最小点覆盖等于最大匹配。
所以跑一遍匈牙利或者网络流就解决问题了。
\(\texttt{Part 3}\):二分图最大权匹配相关知识
二分图最大权匹配指的是:对于一个带权值的二分图,需要找一些匹配边,使得它们权值之和最大。
对于一个二分图,我们可以补充一些节点使得二分图两边点数相同,再连一些权值为 \(0\) 的边。
此时,题目转化我求二分图最大权完美匹配,可以使用 KM 算法 解决。
KM 算法
KM 算法是解决二分图最大权完美匹配的非费用流算法。
他可以在 \(\mathcal{O}(n^3)\) 的时间复杂度内求出二分图的最大权完美匹配。
先说一些定义。
定义
顶标:点的一个标记,满足 \(left_u + right_v \geq w(u,v)\),并不唯一。
相等子图:原图的一个子图,满足子图中任意边满足 \(left_u + right_v = w_{u,v}\)。
交错树:增广路径形成的树。
定理:
对于某组可行顶标,如果其相等子图存在完美匹配,那么,该匹配就是原二分图的最大权完美匹配。
证明:
令 \(val(M)\) 表示完美匹配 \(M\) 的权值和,\(a_i\) 表示 \(i\) 的顶标,则有:
\(val(M)=\sum_{(u,v)\in M} w_{u,v} \leq \sum_{(u,v)\in M} a_u + a_v \leq \sum_{i=1}^n a_i\)
一个相等子图的完美匹配 \(M'\) 的权值和:
\(val(M’)=\sum_{(u,v)\in M’} a_u + a_v = \sum_{i=1}^n a_i\)
所以,任意一组完美匹配的边权和都不会大于 \(val(M')\),故 \(M'\) 就是最大权匹配。
于是,算法流程是这样的:确定顶标 -> 尝试匹配 -> 如果有完美匹配则结束 -> 否则修改顶标 -> 再次尝试匹配 ->・・・・・・
初始顶标不妨设 \(left_u = 0, right_v = \max{\text{(所连边权)}}\)。
调整顶标的目的就是要不断往相等子图内加入新的边。
假设现在需要调整顶标,则说明尝试匹配时匈牙利失败了。
对于匹配失败的那个左部点,他 dfs 时形成了一颗交错树。
容易发现以下结论:
交错树中所有右部点都是左部点通过非匹配边访问到的。
我们考虑如何让一个左部点可以访问到更多的右部点。
我们把交错树中所有左部点顶标 \(i\) 减小一个 \(delta\),所有右部点顶标 \(j\) 增加一个 \(delta\)。
记交错树为 \(T\)。
对于一条匹配边,显然要么 \(i,j \in T\)(即被访问到),要么 \(i,j \notin T\)(即没被访问到)。因此其顶标和不变,所以匹配边仍然是相等子图中的边。
因为左部点是被右部点递归访问的,所以只需要考虑 \(i \in T\)。
-
若 \(i,j \in T\),则顶标和不变,以前能访问到的现在还能访问;
-
若 \(i \in T,j \notin T\),则顶标和变小,之前访问不到的点,现在有可能访问了。
为了保证顶标满足定义,所以我们找到最小的 \(left_u + right_v - w_{u,v}\),作为 \(delta\)。
只要原图存在完美匹配,这样的边一定存在。
上述做法不仅不会破坏之前的结果,还可以使交错树中至少一个左部点可以访问更多的右部点。
不断重复以上过程,直到所有左部点都找到匹配,就解决了问题。
具体实现时,我们可以维护一个数组记录可能更新的 \(delta\) 值,以便快速求出新的 \(delta\)。
时间复杂度 \(\mathcal{O}(n^2m)\)。
考虑到每次修改顶标后,相等子图只会扩大,所以没必要重新进行完整的 dfs。
我们记录一个 \(upd_j\) 表示每个右部点 \(j\) 对应的最小 \(delta\),当一个点无法继续匹配的时候,我们更新顶标,然后直接从最小边开始新的 dfs。
匹配成功后,由于 dfs 不一定从根开始,所以我们无法利用回溯更新增广路,需要记录 \(last\) 数组表示每一个右部点 \(j\) 在交错树中的上一个右部点,沿着 \(last\) 倒退回去即可找到增广路。
时间复杂度降到了 \(\mathcal{O}(n^3)\)。
给出参考代码(可通过模板题 P6577):
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x = 0, f = 1;
char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)){
x = (x<<1) + (x<<3) + (ch^48);
ch = getchar();
}
return x*f;
}
const int N = 1001, M = 1e5 + 1, inf = 1e18 + ~-1;
bool va[N], vb[N]; //是否访问
int n, m;
int la[N], lb[N], w[N][N], last[N], upd[N], match[N];
//la、lb 表示顶标
//w 表示边权
//upd[j] 表示表示每个右部点 j 对应的最小 delta
//last 表示每一个右部点在交错树中的上一个右部点
inline bool dfs(int u, int fa){
va[u] = true;
for(int v = 1; v <= n; v++){
if(!vb[v]){
if(la[u] + lb[v] - w[u][v] == 0){
vb[v] = true;
last[v] = fa;
if(!match[v] || dfs(match[v], v)){
match[v] = u;
return true;
}
}else if(upd[v] > la[u] + lb[v] - w[u][v]){
upd[v] = la[u] + lb[v] - w[u][v];
last[v] = fa;
}
}
}
return false;
}
inline int KM(){
for(int i = 1; i <= n; i++){
la[i] = -inf; lb[i] = 0;
for(int j = 1; j <= n; j++){
la[i] = max(la[i], w[i][j]);
}
}
for(int i = 1; i <= n; i++){
memset(va, 0, sizeof(va));
memset(vb, 0, sizeof(vb));
memset(last, 0, sizeof(last));
memset(upd, 0x7f, sizeof(upd));
// 从右部点 st 匹配的左部点开始 dfs,一开始假设有一条 0 -> i 的匹配
int st = 0; match[0] = i;
while(match[st]){
int delta = inf;
if(dfs(match[st], st)) break;
for(int j = 1; j <= n; j++){
if(!vb[j] && upd[j] < delta){
delta = upd[j];
st = j;// 下一次直接从最小边开始 dfs
}
}
for(int j = 1; j <= n; j++){ //修改顶标
if(va[j]) la[j] -= delta;
if(vb[j]) lb[j] += delta; else upd[j] -= delta;
}
vb[st] = true;
}
while(st){ // 倒推更新增广路
match[st] = match[last[st]];
st = last[st];
}
}
int ans = 0;
for(int i = 1; i <= n; i++) ans += w[match[i]][i];
return ans;
}
signed main(){
n = read(), m = read();
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) w[i][j] = -inf;
for(int i = 1; i <= m; i++){
int u = read(), v = read(), W = read();
w[u][v] = W;
}
printf("%lld\n", KM());
for(int i = 1; i <= n; i++) printf("%lld ", match[i]);
return 0;
}
例题 \(\texttt{9}\)
有 \(n\) 件工作要分配给 \(n\) 个人做。第 \(i\) 个人做第 \(j\) 件工作产生的效益为 \(c_{ij}\)。试设计一个将 \(n\) 件工作分配给 \(n\) 个人做的分配方案,使产生的总效益最小或最大(一个人只能修一个工件)。
\(1 \leq n \leq 50\),\(0 \le c _ {i, j} \le 100\)。
题解
题目:https://www.luogu.com.cn/problem/P4014。
非常裸的二分图最大权完美匹配。
我们把人和工作分别当成左部点和右部点。
跑一遍 KM 算法就可以求出最大值了。
然后整体取负再跑一遍 KM 算法就可以求出最小值了。
\(\texttt{Part 4}\):二分图相关综合例题
这里提供一些二分图相关综合例题。
例题 \(\texttt{10}\)
小 D 有一个长度为 \(n\) 的整数序列 \(a_{1 \dots n}\),她想通过若干次操作把它变成序列 \(b_i\)。
小 D 有 \(m\) 种可选的操作,第 \(i\) 种操作可使用三元组 \((t_i,u_i,v_i)\) 描述:若 \(t_i=1\),则她可以使 \(a_{u_i}\) 与 \(a_{v_i}\) 都加一或都减一;若 \(t_i=2\),则她可以使 \(a_{u_i}\) 减一、\(a_{v_i}\) 加一,或是 \(a_{u_i}\) 加一、\(a_{v_i}\) 减一,因此当 \(u_i=v_i\) 时,这种操作相当于没有操作。
小 D 可以以任意顺序执行操作,且每种操作都可进行无限次。现在给定序列与所有操作,请你帮她判断是否存在一种方案能将 \(a_i\) 变为 \(b_i\)。题目保证两个序列长度都为 \(n\)。若方案存在请输出 YES,否则输出 NO。
数据范围:\(1 \leq T \leq 10\),\(1 \leq n,m \leq 10^5\),\(1 \leq a_i,b_i \leq 10^9\)。
题解
题目:https://www.luogu.com.cn/problem/P6185。
考虑把每个位置当成一个点,把操作 \(1\)「都加 \(1\) 或都减 \(1\)」连边。
操作 \(2\) 的「一个加 \(1\) 一个减 \(1\)」可以转化为两次操作 \(1\)(考虑 \((u,k)+1\),\((k,v)-1\) 等价于 \(u+1,v-1\)),所以把操作 \(2\) 看成两个操作 \(1\) 来连边,可以用虚拟节点辅助。
连边后的图分为很多联通块,对于一个联通块,有以下三种情况:
-
只有一个点,此时这个点如果不是目标值,就判无解。
-
联通块内存在边。显然「都加 \(1\) 或都减 \(1\)」的奇偶性不变。故判断一下「联通块内所有数的和 减去 联通块内所有数的目标值的和」的奇偶性即可,奇数判无解。
-
这是一个没有奇环的图,即二分图(包含于 \(2\) 情况)。显然「都加 \(1\) 或都减 \(1\)」的差不变。所以「二分图两个集合的差」与「二分图两个集合目标值的差」不同时,判无解。
如果判断完所有联通块都没有返回无解,答案就是存在。
例题 \(\texttt{11}\)
给定平面上的 \(N\) 个黑点和 \(N\) 个白点(共 \(2N\) 个点),请找到一种方案,对于每一个黑点,找到一个白点,用线段把黑点和白点连接,保证最后任意两条线段无公共点(不相交)。
保证无三点共线,数据保证有解。
\(1\leq N\leq 100, |x|, |y|\leq 10^4\)。
题解
题目:https://www.luogu.com.cn/problem/UVA1411。
因为三角形两边之和大于第三边,因此所有线段不相交,等价于线段长度和最小。
我们把白色看成左部点,黑色看成右部点。
然后把所有白色点与黑色点连接,边权为平面上的距离。
然后用 KM 算法求二分图最小权匹配就好了。
P.S. 二分图最小权匹配就是取负然后求最大权匹配。
例题 \(\texttt{12}\)
有 \(N\) 个单身的男孩和 \(N\) 个单身女孩,男孩 \(i\) 和女孩 \(j\) 在一起得到的幸福值为 \(H_{i,j}\)。
一个匹配即对这 \(N\) 个男孩女孩的安排:每个男孩恰好有一个女朋友,每个女孩恰好有一个男朋友。
一个匹配的幸福值即这 \(N\) 对男女朋友的幸福值的和。
经典的问题是计算幸福值最大的匹配,即完美匹配。然而完美匹配有时候并不唯一,你需要计算对于所有的完美匹配,其交集是什么。
\(1\leq N \leq 80\),\(0\leq H_{i,j}\leq 5\times10^3\)。
- \(\texttt{Hint: }\) \(\mathcal{O}(n^4)\) 可以过。
题解
题目:https://www.luogu.com.cn/problem/P3967。
第一问显然,考虑第二问。
我们进行 \(n\) 次暴力断掉在第一问中找到的匹配边,跑 \(n\) 遍 KM 算法,若结果变小,那么这条断掉的边一定必须选。
KM 算法在随机数据面前的复杂度为 \(\mathcal{O}(n^3)\),面对特殊构造的数据是 \(\mathcal{O}(n^4)\)。
不过这道题不毒瘤,\(\mathcal{O}(n^4)\) 可过。
例题 \(\texttt{13}\)
有 \(m\) 个椅子在数轴上排列,第 \(i\) 张椅子的坐标为 \(i\)。高桥君等 \(n\) 个人,想坐在椅子上。
高桥君等人中,第 \(i\) 个人想坐在坐标在 \(l_i\) 以下(包括 \(l_i\))的椅子上,或者坐在坐标在 \(r_i\) 以上(包括 \(r_i\))的椅子上。当然,一个的椅子只能坐一个人。
高桥君要增加椅子,使他们都能够坐在椅子上休息。 椅子可以添加到任意的实数坐标上,请求出需要添加椅子数量的最小值。
\(1 \leq n,m \leq 2 \times 10^5,0 \leq li < r_i \leq m + 1\),所有的数都是整数。
题解
题目:https://www.luogu.com.cn/problem/AT_arc076_d。
首先题意转化:在不添加椅子的情况下保证能让最多的人做上椅子。
我们考虑每个人当做左部点,每个椅子当做右部点,能坐就连边,则求出最大匹配就可以了。
但是,目前不存在 \(\mathcal{O}(n)\) 的二分图最大匹配算法,所以不能直接暴力求解。
考虑 Hall 定理推论:
二分图 \(G\) 的最大匹配为 \(|X| - \max(|X'|-|N(X')|)\),其中 \(X\) 是数量较少的集合,\(X'\) 是 \(X\) 的任意子集,\(N(u)\) 表示 \(u\) 的邻居节点集合。
因此最大匹配 \(n - \max(|S|-|N(S)|)\)。
我们根据连边方式把 \(N(S)\) 写成 \(\bigcup_{i \in S}[1,l_i]\cup[r_i,m]\)。
由于不好表示(不连续),因此再写成 \(|N(S)| = m - |\bigcap_{i \in S}(l_i,r_i)|\)。
故最终最大匹配为 \(n - \max(|S|+|\bigcap_{i \in S}(l_i,r_i)|) + m\)。
而我们只需要求出 \(\max(|S|+|\bigcap_{i \in S}(l_i,r_i)|)\)。
考虑使用线段树 + 扫描线。
大概做法就是按照 \(l_i\) 排序,然后一边插入一边计算。
具体做法不是本文重点。
例题 \(\texttt{14}\)
下面是一个经过部分改动的求 \(\gcd\) 的伪代码(其中 \(t\) 是一个初始为空的序列):
function Euclid(a, b):
if a < b:
swap(a, b)
if b == 0:
return a
r = reminder from dividing a by b (即设 r 为 a mod b)
if r > 0:
append r to the back of t (即将 r 插入到 t 的尾部)
return Euclid(b, r)
有一个由数对构成的序列 \(p\),接下来我们对 \(p\) 中每个数对都执行一次上述函数,然后把 \(t\) 重新排列并给定到输入中。
给定 \(n,m\) 和长度为 \(n\) 的序列 \(t\)。
你需要构造一个长度不超过 \(2\times10^4\) 的数对序列 \(p\),满足:
- 每个数对中的元素都是不超过 \(m\) 的正整数。
- 根据序列 \(p\) 可以经过上述操作得到输入中给定的 \(t\)。
有解输出任意一组解,无解输出 -1。
题解
题目:https://www.luogu.com.cn/problem/CF1684G。
注意到数对 \((3x,2x)\) 即往 \(t\) 中添加一个 \(x\)。于是只需要考虑大于 \(\frac{m}{3}\) 的构造。
为了方便,我们称大于 \(\frac{m}{3}\) 的数为大数,反之则称为小数。
注意到:
Euclid(a, b) --> t1
Euclid(b, t1) --> t2
如果 \(t1\)、\(t2\) 都是大数(即 \(t1,t2 > \frac{m}{3}\)),则根据 \(t2 = b \bmod t1\),有 \(b \geq t2+t1,t1 > t2\),即 \(b > \frac{2}{3}m\)。再由 \(t1 = a \bmod b\),可得 \(a > m\),矛盾!
因此一个数对不能生成两个大数。
另一方面,对于大数 \(x\) 和小数 \(y\)(\(x \bmod y = 0\)),构造数对 \((2x+y,x+y)\) 确实可以得到 \(x\) 和 \(y\):
if y|x:
2x+y mod x+y = x
x+y mod x = y
x mod y = 0 (0 isn't in t)
而且一个数对生成一个大数和一堆小数,可以转化为上述构造与一堆单独的小数。因为这样构造后函数的调用次数一定不超过 \(n\)。
于是我们考虑构造如何匹配大数和小数。
我们把大数看做左部点,小数看做右部点,对于大数 \(x\) 和小数 \(y\) 如果满足 \(x \bmod y = 0\) 且 \(2x + y \leq m\),就连边。
然后求二分图最大匹配即可,我们的目标是每个大数都能被匹配(小数可以自己生成)。如果大数匹配失败可以直接判无解。
最后根据匹配的构造使用 \((2x+y,x+y)\) 解决大数,剩余的小数采用 \((3x,2x)\) 即可。
匈牙利算法的最终复杂度是 \(\mathcal{O}(n^3)\),但边不满所以能过,不确定能不能被 Hack(所以还是用网络流吧
网络流复杂度 \(\mathcal{O}(n\sqrt{m}) = \mathcal{O}(n^2)\) 可以通过(实际上建边复杂度就达到 \(\mathcal{O}(n^2)\) 了)。
结语
(学习我校大神的传统艺能)
以上,我们探讨了二分图这一图论的概念、性质以及它的应用场景。
从基础的判定,到求最大匹配,二分图在许多题目中扮演着不可或缺的角色。
随着技术的不断进步,二分图的应用也在不断扩展,从简单的黑白匹配,到复杂的二分图博弈,它都展现出了强大的生命力和灵活性。
我希望本文能够帮助读者更好地理解二分图,激发大家对二分图更深层次探索的兴趣。
在未来的学习和实践中,二分图无疑将成为解决各种问题的有力工具。让我们一起期待二分图在新技术中的应用,以及它如何帮助我们构建更加智能和高效的系统。
感谢您的阅读,如果您对二分图有更深入的问题或想要探讨相关话题,我们欢迎您的反馈和讨论。
改编自:2024 BNDSOJ 论文《用字典树实现平衡树》结语部分 ———— masonxiong。
参考资料
-
二分图最大权匹配 —— OI Wiki。
-
论文《The Dynamic Hungarian Algorithm for the Assignment Problem with Changing Costs》
-
《算法竞赛进阶指南》—— 李煜东 著。
-
2024 BNDSOJ 论文《用字典树实现平衡树》结语部分 —— masonxiong 著。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号