[每日一题] [力扣673] 最长递增子序列的个数 2021.9.20

题目描述

给定一个未排序的整数数组，找到最长递增子序列的个数。

示例 1:

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。

示例 2:

输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。
注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-longest-increasing-subsequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

关联题目

300 最长递增子序列
300 最长递增子序列 2021.9.20

解题思路

首先题目要求求出最长子序列的个数。那想法自然是先通过 300题 类似的做法把最长子序列求出来。
然后再对其进行计数。

这里用dp指最长子序列的动态规划数组
之前自己想的方法也是比较多的，但是并没有能回答正确。
比如直接统计最长严格递增子序列的个数。

如例：
[1,3,5,4,7] dp [1,2,3,3,4]
直接统计4的个数是不对的。因为4有两个来源的方向，一个是从元素5，一个是元素4.
所以应该有两种。

看了题解后也是一知半解不知道为什么计数的数组要定义为这样。有那样的递推公式。
参考题解1
参考题解2

今天看了一本Leetbook 动态规划精讲（一）有所启发写出来分享一下。

动态规划的思考过程应该是不断减少问题的规模，然后不断地通过求解子问题的答案，再统一之后再得到最优的一个解

如300题例子：
[1,3,5,4,7]

1. 考虑把问题规模减少

f(5) = f([1,3,5,4,7])
f(4) = f([1,3,5,4])
f(3) = f([1,3,5])
f(2) = f([1,3])
f(1) = f([1])

2. 分析减少后问题的规模与解的关系

# 这里dp从1下标开始
f(1)  = f([1]) 时 dp[1] = ?  显然dp[1] = 1;
f(2) = f([1,3]) 时dp[2] = ?  由于1 < 3 所以3是下一个递增的元素，所以此时应该dp[2] = dp[1] + 1
f(3) = f([1,3,5]) 时。同上：dp[3] = dp[2] + 1
f(4) = f([1,3,5,4]) 时。由于3 < 4 ， 4是3的递增子序列下一个元素。所以应该在dp[3]的基础上+1
                       而5 > 4所以并不满足递增子序列的下一下元素。
                       dp[4] = dp[2] + 1
                       这里为什么选定3元素对应的dp值呢？因为3是1，3里面最高的。
f(5) = f([1,3,5,4,7]) 。由于 5 < 7 成立，4 < 7 成立
                       所以dp[5] = dp[3] + 1 ，也可以 dp[4] = dp[3] + 1看哪一个更高一些

3. 试写出状态转移方程
   🤔 是否有

for i in range(1,len(nums)):
  max_len = 0
  for j in range(0,i):
    if nums[j] < nums[i]:
      max_len = max(max_len,dp[j])
    dp[i] = max_len

此题目与300类似，cnt也是使用动态规划计算得出。
可以试写两个例子来分析一下这个cnt如何推断出来。

尝试1 动态规划

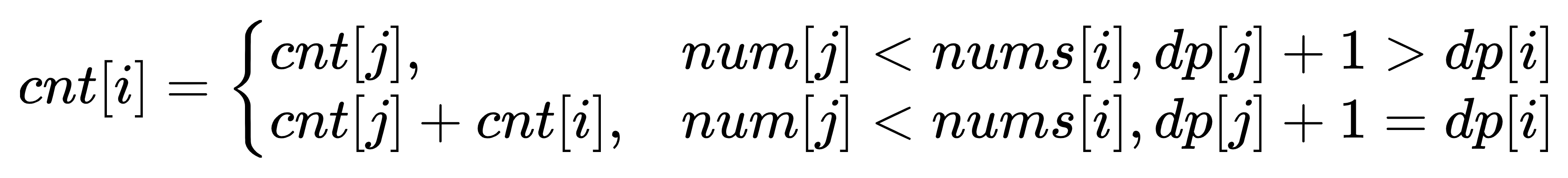
试想一下，当dp[j] + 1 > dp[i] 时，证明最大值需要变化了，那么需要把最大值更新。最大值更新意味着使用的是在原来的cnt的最长递增子序列的元素又加了一个。

当dp[j] + 1 == dp[i] 时，这时找到有一个序列与本序列的dp一样长。所以cnt[i]需要把原来的cnt[j]加上。

class Solution {
public:
    int findNumberOfLIS(vector<int> &nums) {
        if (nums.size() == 1)
            return 1;
        int n = nums.size();
        std::vector<int> dp(n, 1);
        std::vector<int> cnt(n, 1);
        for (int i = 1; i < nums.size(); i++) {
            int max = 0;
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {
                    if (dp[j] + 1 > dp[i]) {
                        dp[i]  = dp[j] + 1;
                        cnt[i] = cnt[j];
                    } else if (dp[j] + 1 == dp[i]) {
                        dp[i] = dp[j] + 1;
                        cnt[i] += cnt[j];
                    }
                }
            }
            dp[i] = max + 1;
        }
        for (auto &i : dp) {
            printf("%d ", i);
        }
        printf("\n");
        for (auto &i : cnt) {
            printf("%d ", i);
        }
        printf("\n");
        int max_len   = *std::max_element(dp.begin(), dp.end());
        int max_count = 0;
        for (int i = 0; i < dp.size(); i++) {
            if (dp[i] == max_len) {
                max_count += cnt[i];
            }
        }
        return max_count;
    }
};