数据结构(4)
树,二叉树,查找算法总结
一.思维导图
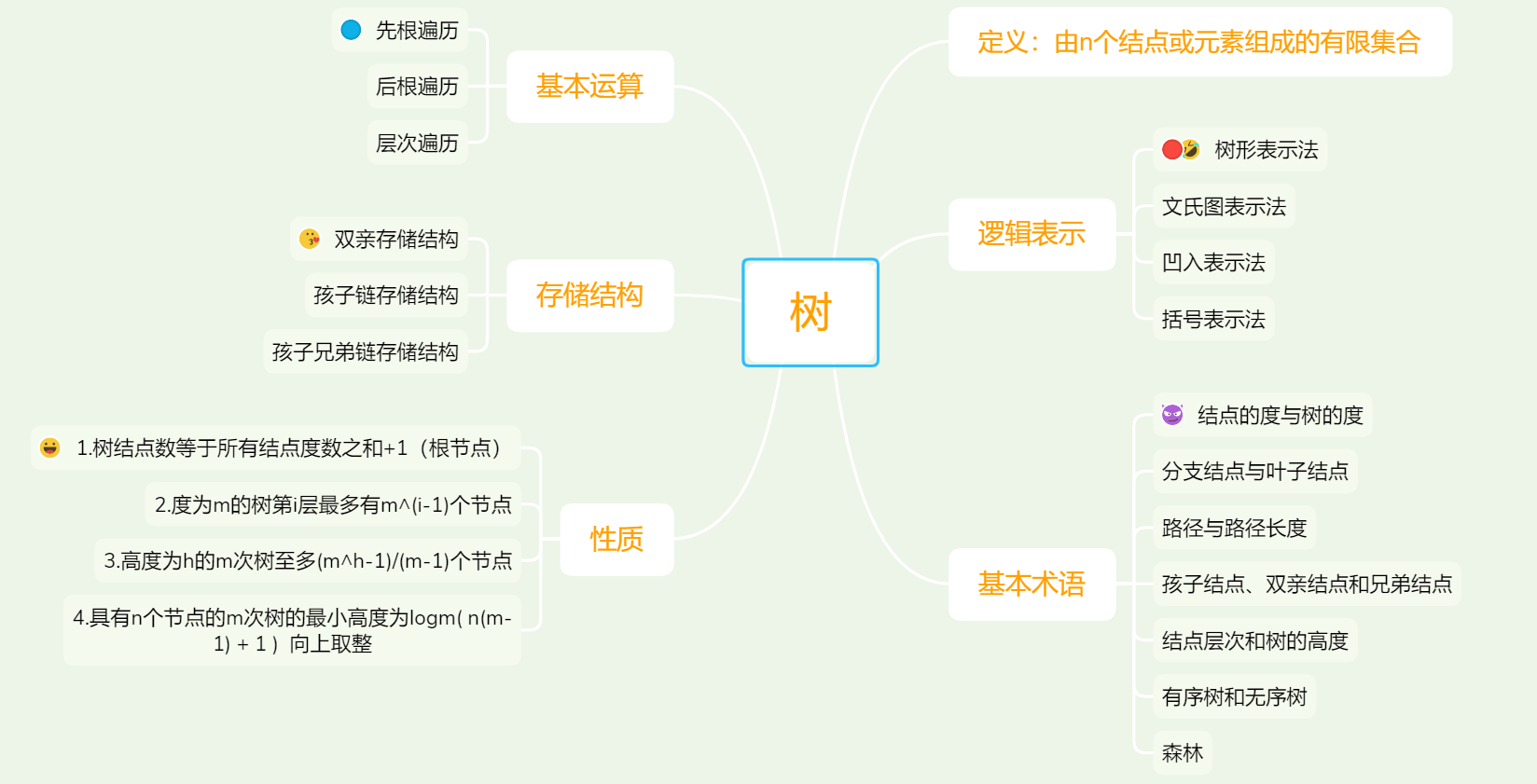

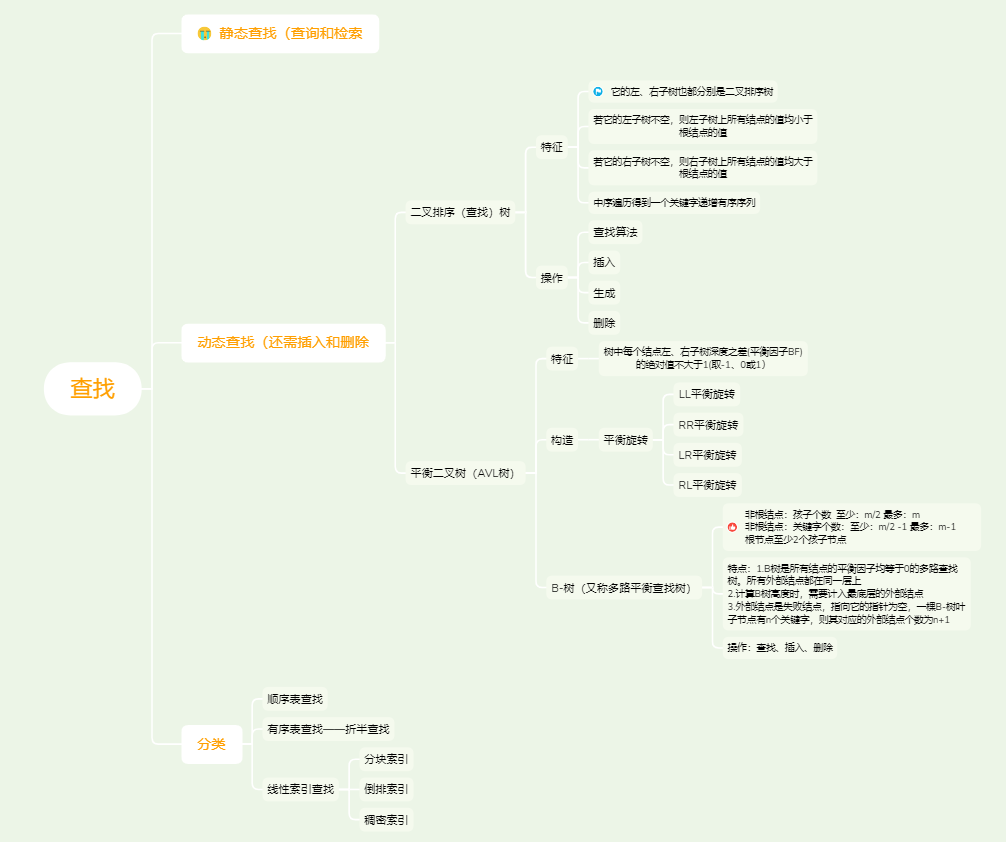
二.重要概念笔记
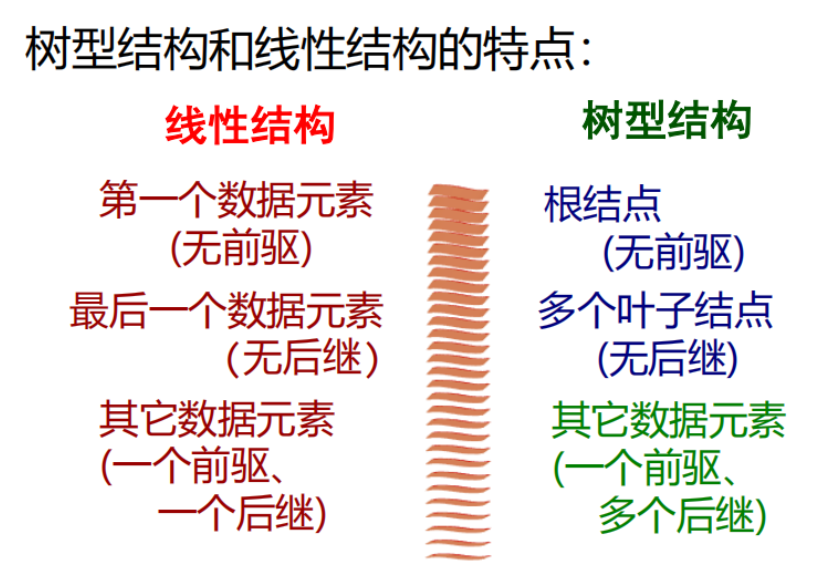
1.树
查找类:
Root(T) //求树的根结点
Value(T, cur_e) //求当前结点的元素值
Parent(T, cur_e) //求当前结点的双亲结点
LeftChild(T, cur_e) //求当前结点的最左孩子
RightSibling(T, cur_e)//求当前结点的右兄弟
TreeEmpty(T) // 判定树是否为空树
TreeDepth(T) // 求树的深度
TraverseTree(T) //遍历
插入:
InitTree(&T) // 初始化置空树
CreateTree(&T, definition) // 按定义构造
Assign(T, cur_e, value) // 给当前结点赋值
InsertChild(&T, &p, i, c) // 将以c为根的树插入为结点p的第i棵子树
删除:
ClearTree(&T) //将树清空
DestroyTree(&T) //销毁树的结构
DeleteChild(&T,&p,i)//删除结点p的第i个孩子
2.二叉树
① 两类特殊的二叉树:
满二叉树:指的是深度为k且含有2k-1个结点的二
叉树。
完全二叉树:树中所含的n个结点和满二叉树中
编号为 1 至 n的结点一一对应。
②完全二叉树具有n个结点的完全二叉树的深度为 log2n+1

③算法递归
void Preorder(BiTree T)
{ //先序遍历二叉树
if (T) {
cout << T->data; // 访问结点
Preorder(T->lchild); // 遍历左子树
Preorder(T->rchild); // 遍历右子树
}
}
void Inorder(BiTree T)
{ // 中序遍历二叉树
if (T) {
Inorder(T->lchild); // 遍历左子树
cout << T->data; // 访问结点
Inorder(T->rchild); // 遍历右子树
}
}
void Postorder(BiTree T)
{ // 后序遍历二叉树
if (T) {
Postorder(T->lchild); // 遍历左子树
Postorder(T->rchild); // 遍历右子树
cout << T->data; // 访问结点
}
}
④非递归算法
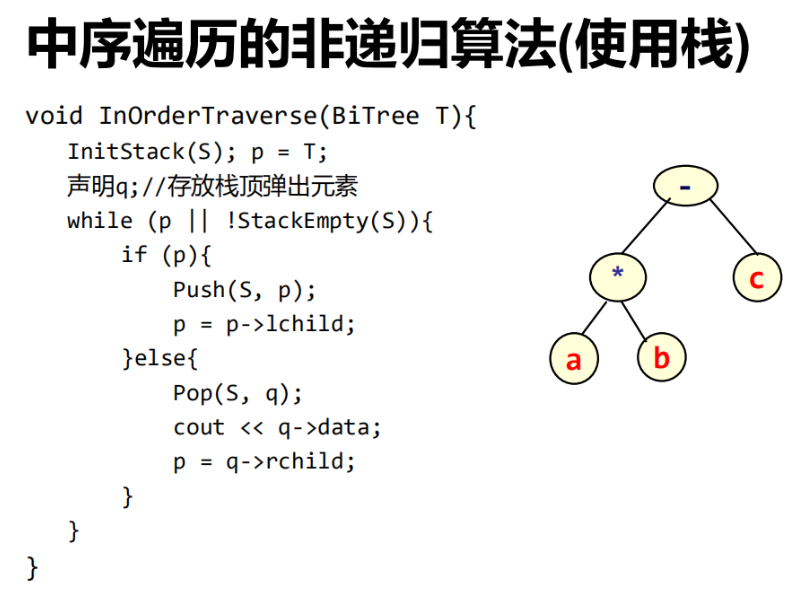
⑤线索链表的遍历算法:
如何找到下一节点?
for(p = firstNode(T);p;p = Succ(p))
Visit(p);
⑥中序线索化链表的遍历算法
1.中序遍历的第一个结点 :左子树上处于“最左下”(没有左子树)的结点。
2.在中序线索化链表中结点的后继 :
若无右子树,则为后继线索所指结点;否则为对其右子树进行中序遍历时访问的第一个结点。

⑧树、二叉树、森林的相互转化
- 树转换为二叉树
1)加线:在所有相邻的兄弟之间各加一连线
2)抹线:每个非终端结点只保留它到最左孩
子的连线,去除它与其余孩子之间的连线;
3)旋转调整:以根结点为轴心,顺时针旋转
一定角度,使结点按层次排列 - 二叉树转换为树
1)加线:若p结点是双亲结点的左孩子,则将p的右孩子、右孩子的
右孩子、…….沿分支找到的所有右孩子,都与p的双亲用线连起来
2)抹线:抹掉原二叉树中双亲与右孩子之间的连线
- 调整:将结点按层次排列
- 森林转换为二叉树
1.转换:将各棵树分别转成二叉树;
2.加线:把每棵树的根结点用线连起来;
3.调整:以第一棵树的根结点作为二叉
树的根结点,将结点按层次排列
⑨构造哈夫曼树

三.查找
①顺序表查找
int Search_Seq(SSTable ST, KeyType key) {
ST.elem[0].key = key;
// 从后往前找
for (i = ST.length; ST.elem[i].key != key; --i);
return i;
②有序表查找:时间复杂度O(log2n)
int Search_Bin(SSTable ST, KeyType key) {
low = 1; high = ST.length; // 置区间初值
while (low <= high) {
mid = (low + high) / 2;
if (EQ(key, ST.elem[mid].key) )
return mid; // 找到待查元素
else if (LT(key, ST.elem[mid].key))
high = mid - 1; // 继续在前半区间进行查找
else low = mid + 1; // 继续在后半区间进行查找
}
return 0; // 顺序表中不存在待查元素
}
③ 二叉排序树查找性能分析含有n个结点的二叉排序树的平均查找长度和树的形态有关
④B-树的查找:
从根结点出发,沿指针搜索结点和在结点内进行顺序(或折半)查找两个过程交叉进行;
若查找成功,则返回指向被查关键字所在结点的指针和关键字在结点中的位置;若查找不成功,则返回插入位置。
Result SearchBTree(BTree T, KeyType K) {
p = T; q = NULL; found = FALSE; i = 0;
while (p && !found) {
i = Search(p, K);
// 在p->key[1..keynum]中查找 i ,p->key[i]<=K<p->key[i+1]
if (i > 0 && p->key[i] == K) found = TRUE;
else { q = p; p = p->ptr[i]; } // q 指示 p 的双亲
}
if (found) return (p, i, 1); // 查找成功
else return (q, i, 0); // 查找不成功
} // SearchBTree
⑤B-树的插入
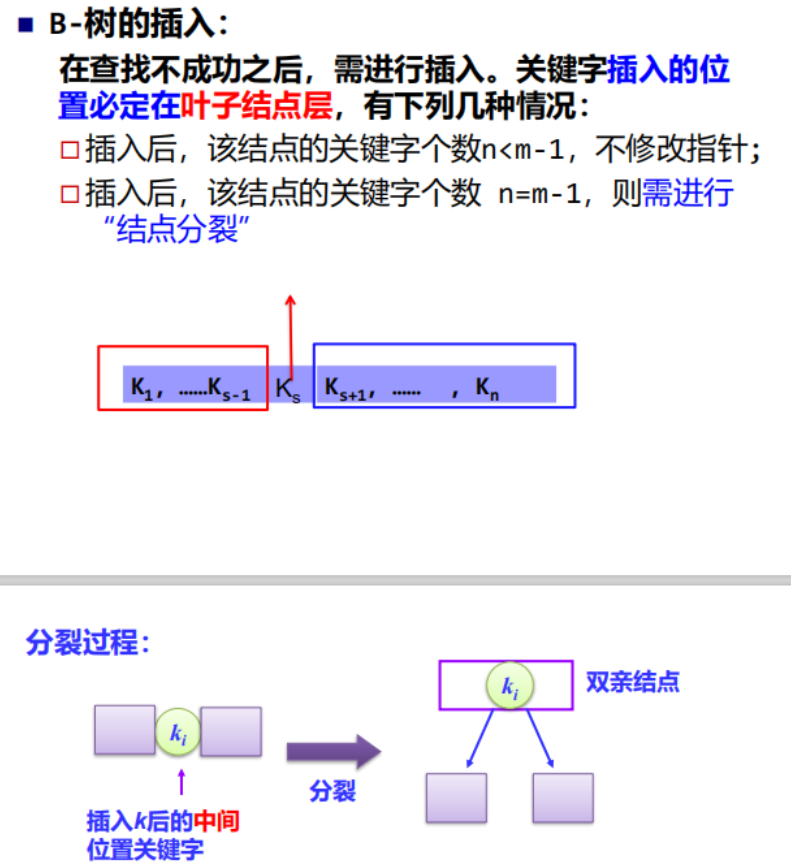
⑥B-树的删除
首先必须找到待删关键字所在结点,并且要求删除之后,结点中关键字的个数不能小于[m/2]-1;
否则, 要从其左(或右)兄弟结点“借调”关键字,若其左和右兄弟结点均无关键字可借(结点中只有最少量的关键字),则必须进行结点的“合并”。
⑦B+树
1.每个分支节点至多有m棵子树
2.根节点或者没有子树,或者至少有两棵子树
3.除根节点,其他每个分支节点至少有[m/2]棵子树;
4.有n棵子树的节点有n个关键字
5.叶子节点包含全部关键字及指向相应记录的指针
6.所有分支节点(可看成是分块索引的索引表)

⑧哈希函数构造方法
直接定址法、数字分析法、平方取中法、折叠法 、除留余数法、随机数法
!除留余数法:
设定哈希函数为:H(key) = key MOD p
其中,p≤m (表长) 并且p应为不大于 m 的素数或是不含 20 以下的质因子
⑨处理冲突方法
开放定址法 、再哈希法、链地址法、建立公共溢出区
1.开放地址法:线性探测再散列、二次探测再散列、随机探测再散列
2.链地址法(拉链法):将所有哈希地址相同的记录都链接在同一链表中
⑩哈希表的查找
Status SearchHash(HashTable H, KeyType K) {
H0 = Hash(K); // 求得哈希地址H0
if (HT[H0].key == NULLKEY) return -1;
else if (HT[H0].key == key) return H0;
else {
for (int i = 1; i < m; i++) {
Hi = collision(H0, i);//利用再探测方法确定Hi
if (HT[Hi].key == NULLKEY) return -1;
else if (HT[Hi].key == key) return Hi;//找到
}
return -1;
}
}
三.疑难解惑
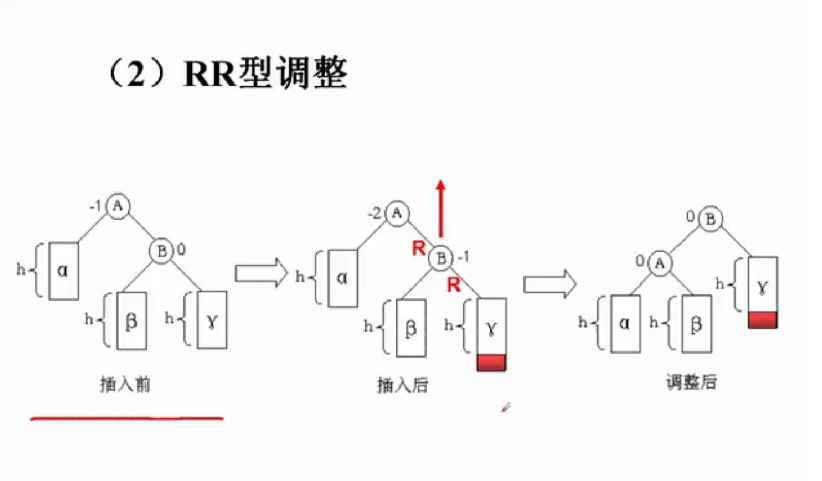
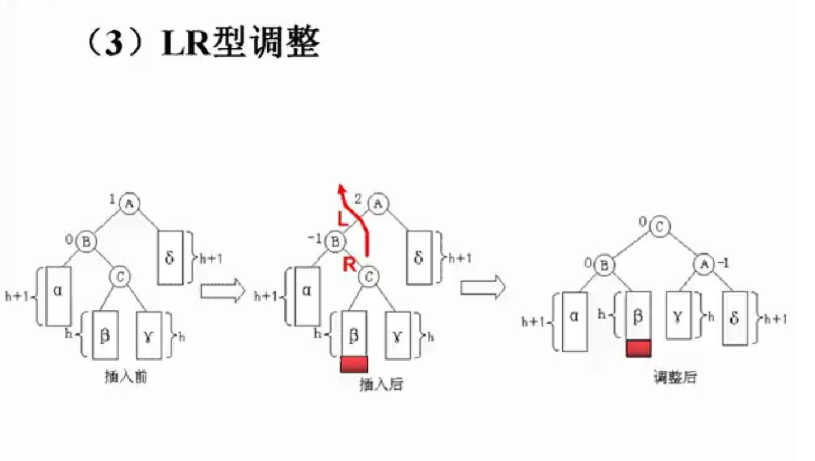
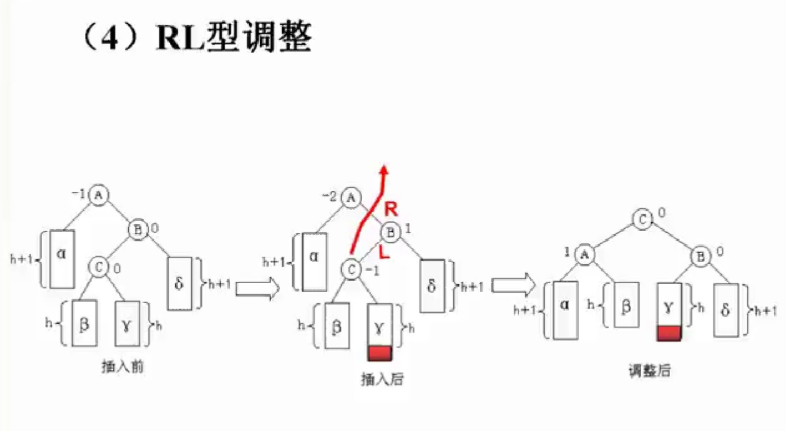
平衡二叉树中插入新节点的调整:
不太理解课堂上的平衡旋转,这种调整更直观易懂





 浙公网安备 33010602011771号
浙公网安备 33010602011771号