数构作业（2）

二叉排序树实现

一.伪代码

1.SearchBST(T, key)

SearchBST(T, key) {
	if ( T空 || T的关键字为key)    //递归终结条件
		return;
	if (T的关键字 < key)
		return(T->lchild, key);  //左子树中递归查找
	else
		return(T->rchild, key);  //右子树中递归查找
}

2.InsertBST(T,key)

InsertBST(T, key) {
	if (T为空) {  //原树为空，新插入的作为根节点
		T=(BSTree)malloc(sizeof(BSTNode));
		T->key = key;
		初始化T;
	}
	else if (key == T的关键字) //存在相同关键字节点，返回0
		return 0;
	else if (key < T的关键字)
		return InsertBST(T->lchild, key);   //插入左子树中
	else
		return InsertBST(T->rchild, key);   //插入右子树中

3.CreateBST(T)

CreateBST(T,n)
{
初始化T树为空；
while (循环n次)
{
	InsertBST(T,关键字)；	
}
return;
}

4.DeleteBST(T，key)

（查找并删除二叉排序树节点的递归算法）

DeleteBST(T，key) {
	if (T为空) return 0;  //空树删除失败
	else
	{
		if (k < T的关键字) return DeleteBST(T->lchild，key);
		        //递归在左子树中删除节点
		else if (k > T的关键字) return DeleteBST(T->rchild, key);
		        //递归在右子树中删除节点
		else
		{
			Delete(T);  //调用Delete(T)函数删除节点
		}
	}
}

(删除二叉排序树p节点算法）

void Delete(BSTNode *&p) {  //从二叉排序树中删除*p节点
	BSTNode* p;
	if (p的右子树为空) {
		q = p;p = p->lchild;
		          //其左子树根节点放在被删节点位置上
		删除q;
	}
	else if (p的左子树为空) {
		q = p;p = p->rchihld;
		          //其左子树根节点放在被删节点位置上
		删除q;
	}
	else Delete1(p,p->lchild)
	              //*p节点既有左子树又有右子树的情况
}

（删除二叉排序树中均有左右子树的算法）

void Delete1(BSTNode* p，  BSTNode*& r)
//当被删*p结点有左右子树时的删除过程
{
    BSTNode* q;
    if (r右孩子不为空)
        Delete1(p，r->rchild);	//递归找被删结点左子树的最右下结点（前驱结点)
    else  		                //找到最右下节点*r
    {
        将* r的关键字赋给* P;
        q = r;r = r->lchild;
        删除q;
    }
}

二.代码实现

1.二叉排序树节点定义

typedef struct BSTNode  
{  
    int key;  
    struct node*lchild, *rchild;  
} BSTNode;

2.main函数

int main(){
 printf("请输入关键字\n");
 CreatBST(T);
 printf("二叉排序树的中序遍历序列:\n");
 InOrderTraverse(T);
 int n;
 printf("输入要查找的数据：\n");
 while(scanf("%d",&n) != EOF && n){
  if(SearchBST(T, n))
   printf("输出查找的结果：该结点已找到。\n");
  else
   printf("输出查找的结果：该结点未找到。\n");
 }
    return 0;
}

3.中序遍历

void InorderTraverse(BSTree T)//中序遍历
{  
     if(T)
     {  
          InorderTraverse(T->lchild);
          printf("%d ",T->key);
          InorderTraverse(T->rchild);
     }
}

4.SearchBST(T, key)

int SearchBST(BSTree T,int key)
{
    if (T == NULL || T->key == k)
        return T;
    if (k < T->key)
        return SearchBST(T->lchild, k);
    else
        return SearchBST(T->rchild, k);
}

5.InsertBST(T,key)

int InsertBST(BSTNode T,int key)
{
    if (T == NULL)
    {
        T=(BSTree)malloc(sizeof(BSTNode));
        T->key = key;
        T->lchild = NULL;
        T->rchild = NULL;
    }
    else if (key == T->key)
        return 0;
    else if (key < T->key)
        InsertBST(T->lchild,key);
    else
        InsertBST(T->rchild,key);
}

6.CreateBST(T)

int CreatBST(BSTree T)
{
    T = NULL;
    int i = 0;
    while (i < n)
    {
        InsertBST(T,A[i]);
        i++;
    }
    return T;
}

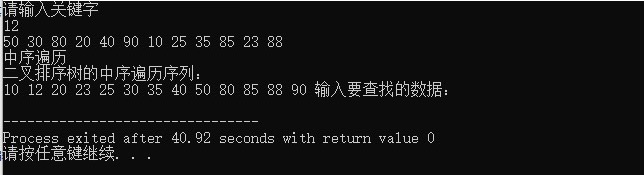
使用“50 30 80 20 40 90 10 25 35 85 23 88”创建BST，并中序输出该BST

7.DeleteBST(T，key)

（查找并删除二叉排序树节点的递归算法）

int DeleteBST(BSTNode &T,int key)  
{
    if (T == NULL) return 0;	
    else
    {
        if (k < T->key) return DeleteBST(T->lchild,k);
        
        else if (k >T->key) return DeleteBST(T->rchild,k);
        
        else   
        {
            Delete(T);    
            return 1;
        }
    }
}

(删除二叉排序树p节点算法）

void Delete(BSTNode *&p)   	 
{
    BSTNode* q;
    if (p->rchild == NULL)        	
    {
        q = p; p = p->lchild;		
        free(q);
    }
    else if (p->lchild == NULL)    	
    {
        q = p; p = p->rchild;	
        free(q);
    }
    else Delete1(p,p->lchild);
}

（删除二叉排序树中均有左右子树的算法）

void Delete1(BSTNode *p,BSTNode *&r)
{
    BSTNode* q;
    if (r->rchild != NULL)
        Delete1(p,r->rchild);	
    else  		              
    {
        p->key = r->key;  
        p->data = r->data;   
        q = r; r = r->lchild;          
        free(q); 	              
    }
}